Исследование методов квантования сигналов. Моделирование ADC

 

2.2 Предварительное задание. Изучить методы квантования сигналов. Моделирование ADC

В любую систему информация поступает в виде сигналов. Различные параметры физических процессов с помощью датчиков обычно преобразуются в электрические сигналы. Как правило, ими являются непрерывно изменяющиеся ток или напряжение, но возможно поступление и импульсных сигналов, как, например, в радиолокации. Печатный текст отображается буквами, цифрами и другими знаками.

Хотя поступающую информацию можно хранить, передавать и обрабатывать как в виде непрерывных, так и в виде дискретных сигналов, на современном этапе развития информационной техники предпочтение отдается дискретным сигналам, поэтому сигналы, как правило, преобразуются в дискретные. С этой целью каждый непрерывный сигнал подвергается операциям квантования по времени (дискретизации) и по уровню.

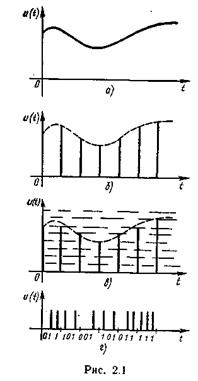
Под дискретизацией подразумевают преобразование функции непрерывного времени в функцию дискретного времени, представляемую совокупностью величин, называемых координатами, по значениям которых исходная непрерывная функция может быть восстановлена с заданной точностью. Роль координат часто выполняют мгновенные значения функции, отсчитанные в определенные моменты времени.

Под квантованием подразумевают преобразование некоторой величины с непрерывной шкалой значений в величину, имеющую дискретную шкалу значений. Оно сводится к замене любого мгновенного значения одним из конечного множества разрешенных значений, называемых уровнями квантования.

Изменение вида сигнала u (t) (рис. 2.1, а) в результате проведения операции дискретизации показано на рис. 2.1,б, а в результате совместного проведения операций дискретизации и квантования – на рис. 2.1, в.

Число уровней квантования на рис. 2.1, в равно 8. Обычно их значительно больше. Передача такого множества различных по уровню импульсов даже на небольшие расстояния применяется крайне редко. Если провести нумерацию уровней, то их передача сведется к передаче чисел. Тогда, выразив эти числа в какой-либо системе счисления, можно обойтись меньшим множеством передаваемых сигналов. Как правило, дискретный сигнал преобразуется в последовательность чисел, выраженных в двоичном коде. Каждое дискретное значение сигнала представляется в этом случае последовательностью сигналов двух уровней. Наличие или отсутствие импульса на определенном месте интерпретируется единицей или нулем в соответствующем разряде двоичного числа.

Цифровая форма представления сигнала u (t) (рис. 2.1, а) показана на рис. 2.1, г. Для восьми уровней достаточно трех двоичных разрядов. Импульсы старших разрядов расположены крайними справа.

При передаче и обработке информации в цифровой технике существует принципиальная возможность снижения вероятности получения ошибочного результата до весьма малых значений. Она возникает потому, что при использовании дискретных сигналов, во-первых, применимы такие методы кодирования, которые обеспечивают обнаружение и исправление ошибок, а во-вторых, можно избежать свойственного аналоговым сигналам эффекта накопления искажений в процессе их передачи и обработки, поскольку квантованный сигнал легко восстановить до первоначального уровня всякий раз, когда величина накопленных искажений приблизится к половине кванта. Практическая реализация указанных методов наиболее эффективна при минимальном числе уровней, равном двум.

Дискретизация по частотному критерию. Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром в наиболее четкой форме сформулировано и доказано акад. В. А. Котельниковым в виде теоремы, получившей в отечественной литературе его имя*.

* В зарубежной литературе эту теорему называют теоремой Найквиста или просто теоремой отсчетов.

Теорема Котельникова. Теорема устанавливает прин­ципиальную возможность полного восстановления детер­минированной функции с ограниченным спектром по ее отсчетам и указывает предельное значение интервала времени между отсчетами, при которой такое восстанов­ление еще возможно. Она формулируется следующим образом: функция u (t), допускающая преобразование Фурье иимеющая непрерывный спектр, ограниченный полосой частот от 0 до F _c = w_c/(2p), полностью опре­деляется дискретным рядом своих мгновенных значений, отсчитанных через интервалы времени

D t =1/(2 F _c)

Физическая основа теоремы выявляется при рассмот­рении связи между формой функции и шириной ее спектра. Только в случае, когда спектр функции без­граничен, ее значения в сколь угодно близкие моменты времени могут изменяться произвольно (корреляционная связь между ними отсутствует).

Рис.2.2

 

Сокращение высоко­частотной части спектра до граничной частоты ω₁ рав­нозначно устранению из временной функции выбросов, которые могли быть сформированы этими высокочас­тотными составляющими (рис. 2.2, а). При меньших гра­ничных частотах ω₂ (рис. 2.2, б) и ω₃ (рис. 2.2, в) имеем бо­лее сглаженные функции времени. Поскольку значения этих функций в моменты времени u (t₁) и u (t₁ + Δ t)в преде­лах некоторого интервала Δ t не могут изменяться суще­ственно, можно ограничиться значениями функции, взя­тыми через интервалы Δ t (отсчетами).

 

 

2.3 Рабочее задание

 

В этом разделе мы будем использовать квантователь из библиотеки функциональных значков SystemView, чтобы квантовать входной сигнал на фиксированное количество битов. Моделирование в предыдущих случаях входные сигналы различных лексем были с точностью плавающей точки, поэтому для большинства целей мы можем предположить, что (заметного) квантования нет.

Квантование сигнала

Соберите схему, приведенную на рисунке 2.1.

Установите следующие параметры в системе.

 

Системное время
Частота дискретизации, Гц
Число отсчетов
Источник пилообразного сигнала
	Amp = 1,875 v
	Freq = 5 Hz
	Offset = -1 v
	Phase = 0 deg
	Max Rate = 1e+3 Hz
Квантователь
	Bits = 4
	Max Input = ±1 v
	Signed Integer Output
	Max Rate = 1e+3 Hz
Усилитель	Gain = -125e-3
	Gain Units = Linear
	Max Rate = 1e+3 Hz

 

Система берет (с точностью плавающей точки) квантованный выходной сигнал генератора пилообразного сигнала с амплитудой напряжения 1,875 В и преобразует его в целое квантованное число. Все источники выходных сигналов в SystemView, по умолчанию установлены на точность с плавающей точкой (исключая, конечно, источники, которые считываются из файла, которые могут быть установлены на точность с фиксированной точкой).

 

Рисунок 2.1

Рисунок 2.2 - Диалоговое окно квантователя
и соответствующие характеристики

ввода/вывода

 

(а) Просмотрите параметры значка 4-х битного квантователя и убедитесь, что имеет входные/выходные характеристики показанные на рисунке 2.2;

Обратите внимание, входной квантователь является восьмибитным, поэтому вторичная амплитуда дополнения находится в пределах от -2³ до 2³, например: -8 до +7.

(б) Запустите систему и затем в окне анализа убедитесь, что значения выборок такие, как предполагались на выходе квантователя рассмотренного выше. (Не забудьте нажать мерцающую синим цветом кнопку «Загрузить обновленные данные блока» , чтобы увидеть обработанные данные только прошедшего процесса моделирования);

(в) Определите погрешность квантования, вычисление которой осуществляется модулями 3, 4 и 5. Объясните полученные результаты;

(г) Модифицируйте параметры квантователя так, чтобы обеспечить трехбитное квантование (8 уровней как показано на рисунке 2.3) с таким же ±1 колебанием напряжения как раньше. Запустите систему и убедитесь, что результаты такие, как предполагалось, и совпадают с данными таблицами, показанными на рисунке 2.3;

(д) Модифицируйте систему так, чтобы амплитуда пилообразного сигнала на входе была равна 2 В. Запустите систему и обратите внимание на эффект «сжимания» ADC. Это происходит потому, что присутствует проблема нелинейности, которая появляется тогда, когда входное напряжение на ADC слишком высокое;

(е) Обратите внимание, что в диалоговом окне параметров квантователя, можно настроить вывод так, что он будет выводиться в форме с плавающей точкой или как целое число. Произвести такую настройку можно при помощи радио-кнопок показанных на рисунке 2.2. Теперь установите форму вывода «с плавающей точкой», запустите процесс моделирования и объясните то, что теперь показывается на выходе.

Рисунок 2.3 - 3 битный квантователь, характеристики ввода-вывода

 

(ж) Измените модуль генератора прямоугольных импульсов на генератор синусоидальных сигналов (ГСН), запустите систему повторно при значении выходных напряжений ГСН, равных 1,75, 1,875 и 2,0 В. Объясните полученные результаты.