Знаходження най коротшої відстані між двома вузлами на мережі доріг

Це одна з перших транспортних задач, що були вирішені методи ДП[12].

Нехай відома мережа автомобільних доріг, яка з'єднує пункти А і Б. Ця мережа складається із сукупності вузлів і з'єднуючих їх доріг. Поставимо задачу пошуку найкоротшого шляху між пунктами А і Б (див. рис.7.1).

 

 

Рис.7.1 До визначення найкоротшого шляху

 

Рухаючись від останнього кроку до першого (від Б до А), знайдемо умовно оптимальне рішення на кожному кроці.

VІ-й крок. На цьому кроці є одна умовна крапка. Припустимо, що ми вже потрапили в цю крапку (незалежно як) і будемо намагатися потрапити в кінцеву крапку Б. Є тільки один шлях, тому це і буде найкоротша відстань =12 (оцінку цієї вузлової крапки змінимо 12).

V - крок. На цьому кроці маємо 3 крапки. Якщо ми потрапимо (незалежно як) у верхню крапку, то найкоротша відстань до Б буде дорівнює 13,для другої крапки 10, для третьої - 9, покажемо стрілками напрямок руху в крапку В.

IV - крок. На цьому кроці маємо дві крапки. З верхньої країн виходить три напрямки. Необхідно вибрати оптимальний напрямок. Якщо рухатися в напрямку крапки 13, то відстань до крапки Б, буде 6+(13)=19.

Якщо рухатися в напрямку крапки з оцінкою (10), то відстань до неї буде дорівнює 5 + (10) = 15; а якщо в напрямку крапки з оцінкою (9), 8+(9)=17 нас цікавить напрямок, який дасть мінімальну оцінку, тому змінимо оцінку цієї крапки, рівної мінімальній з перелічених (15). Аналогічно знаходимо оцінку для другої крапки кроку IV 6+(10)=16; 2+(9)=11; 7+(12)=13.

Мінімальне значення в напрямку крапки (9) далі буде дорівнює (11).

Оптимальні значення позначимо стрілками.

III-крок. На цьому кроці одна вузлова крапка з якої виходить три напрямки

3+(13)=16; 4+(10)=14; 11+(9)=20.

Мінімальну оцінку (14) одержимо рухаючи у вузлову крапку з оцінкою (10).

II – крок. На цьому кроці 3 вузлові крапки:
Для верхньої: 7+(14)=21;

Для другої: 5+(14)=19; 9+(15)=24; 10+(П)=21. мінімальна оцінка (19) у напрямку крапки з оцінкою (14;

Для третьої: 4+(15)=19; 5+(11)=16.

Умовно - оптимальної є оцінка (13) і умовно - оптимальним управлінням

- рух у кутову крапку з оцінкою (11).

І – крок містить 4 можливі напрямки:

3+(21)=24; 6+(14)=20; 4+(19)=23; 8+(16)=24.

Мінімальна сума (20) у напрямку крапки з оцінкою (14).

Таким чином, оцінка (20) для початкової крапки є найкоротшою відстанню між А і Б. Для вибору оптимального управління (вибору найкоротшого напрямку руху) необхідно знайти такий шлях від А до Б, на якому не перериваються стрілки. Таким шляхом буде

 

А→(14) →(10) →В.

 

Варто мати на увазі, що потрапивши в будь-яку крапку, ми завжди знайдемо найкоротший маршрут у Б. Наприклад, із крапки (16) таким маршрутом буде: (16) → (11) → (9) → Б, з відстанню, яка дорівнює 11 + 15=26.

Відзначимо, що цей алгоритм обчислення найкоротшої відстані зветься алгоритмом дослідження всіх можливих шляхів або алгоритмом Кука і Холсея (по імені його авторів).

 

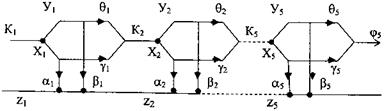
Задачі розподілу ресурсів

При рішенні подібних задач широко використається ДП. Словесно ми вже описали алгоритм рішення. Спробуємо формалізувати і вирішити вказану задачу, спираючись на алгоритм ДП [12].

Припустимо, що на розвиток АТП відпущена певна сума коштів К, яку необхідно розподілити між двома АТП. Ефективність вкладення коштів у перше підприємство оцінюється коефіцієнтом річного прибутку α, у друге - β, причому α < 1 і β<1 і дорівнюють відповідно α=0,4 β =0,5.

Наприкінці кожного року відбувається зменшення первісної суми законом φ((х)=γх; φ(у)=θу, γ=0,8; θ=0,75 (х - сума капіталовкладень у перше підприємство, у - в друге).

Суми, що залишилися, наприкінці кожного року заново перерозподіляються. Обумовимо також, що сума, що залишилася наприкінці кожного року до прибутку не додається.

Необхідно знайти такий розподіл капіталовкладень в перше та в друге підприємство, при якому досягається максимальна сума прибутку за всі 5 років. Неважко уявити, що поставлена задача є класичною задача оптимізації багатокрокових процесів, саме яку доцільно вирішувати застосуванням ДП.

Рішення

 

Представимо функціональну модель задачі у наступному вигляді (рис.7.2).

 

Рис.7.2 Функціональна модель задачі ДП

Вузловими крапками моделі є крапки розподілу суми коштів K_і між підприємствами. Практично це початок кожного календарного року. Таких кроків буде 5. Далі для спрощення виразимо у_і через х_і тобто у_і = к_і — х_і. Записуємо функцію переходу ψ_і виграш z _і для кожного з етапі починаючи, як це витікає з методу ДП, з п'ятого (останнього) етапу.

Етап 5

З огляду на те, що у₅=к₅-х₅ і враховуючи а=0,4 β=0,5 γ=0,8 θ=0,75 запишемо рівняння переходу:

 

ψ₅=γх₅+ θу₅=(γ-θ)х₅+θК₅=0,05х₅+0,75К₅

 

За умовою цей залишок у прибуток не включається.

Величина отриманого прибутку протягом цього року:

 

z₅=αx₅₊βy₅=(α-β)x₅+βx₅=-0,1x₅+0,5y₅.

 

Шукаємо максимум цього прибутку:

Z₅ =max [-0,1х₅+0,5у₅]=0,5К₅,

якщо х₅=0, у₅=К₅.

Етап 4.

Робимо аналогічні дії:

 

ψ₄=γх₄+θу₄=(γ-θ)х₄+θК₄=0,05х₄+0,75К₄=К₅,

 

оскільки це те, що залишилося після 4го року).

z₄=αx₄+βy₄=z_5max=(α-β)x₄+βK₄+z_5max,

 

тому що прибуток за четвертий рік додається до прибутку 5-го року. Враховуючи, що z₅max=0,5K₅:

 

Z₄=max (-0,1x₄+0,5K₄+0,5K₅).

 

Підставимо значення К₅ і отримаємо для сумарного прибутку за 4-й і 5-й роки:

 

Z₄=max [-0,1х₄+0,5К₄+0,5(0,05х₅ +0,75К₄)] (при 0<х₄<К₄)→

Z₄=max [0,875К₄ - 0,095х₄] →

Z_4max=0,875К_4,

 

якщо х₄=0 і у₄-К₄

 

Етап 3.

ψ₃=К₄=0,05х₃+0,75К₃

z₃=(α -β)х₃+βу₃+z_4тах.

З урахуванням, що z_4max=0_!87 5 К₄ одержимо:

 

Z₃=(-0,1x₃+0,5K₃+0,875K₄).

Враховуючи К₄=0,05х₃+0,75К₃, одержимо:

Z₃=(1,1K₃+ 0,02х₃) ( при 0<х₃<К₃) →

Z_3max,=1,12K₃,

 

якщо х₃=К₃ (максимально можливе значення) y₃=0/

Етап 2.

Робимо як завжди:

ψ₂=К₃=0,05х₂+0,75К₂;

z₂=0,4x₂+0,5(K₂-x2)+z_3max →

Z_2Max = мах [1,34до₂ - 0,044x2] (при 0<х2<К₂) →

Z_2max,=1,34K₂,

 

якщоx₂=0 і y₂=K₂

Етап 1.

По аналогії з попередніми етапами:

ψ ₁=0,05x₁+0,75K₁=K₂

z₁=0,4xi+0,5(K₁-x₁)+z_2max

Z_1max=max[1,505K₁ - 0,023x₁] (npu 0<x₁< K₁) →

Z_1max=1,505K_}=1,505K,

 

при х₁=0 і у₁=К (тому що K₁=K).

Отже: максимальний прибуток діяльності 2-х підприємств за 5 років буде дорівнювати 1,505 від суми первісного вкладення, якщо на 1 і 2 роки усю суму капіталовкладень вкладати в друге підприємство, на 3-му році в перше, а на 4 і 5 роках - знову в друге підприємство.

Така стратегія оптимального управління розвитком 2х підприємств.

Досі ми розглядали простий випадок, коли αі β однакові для всіх етапів. Зустрічаються задачі, де αі β на кожному етапі різні (це є задача розподілу ресурсів з неоднорідними етапами). Рішення цієї задачі практично не відрізняється від розглянутої раніше і вирішується аналогічно із застосуванням поточних значень α _i і β_i на кожному i -му розвитку підприємства.

Зустрічаються також задачі розподілу ресурсів, коли отриманий прибуток відчисляється не повністю, а частково вкладається в розвиток виробництва. У цьому випадку відрахований прибуток на будь-якому і -мукроці записується у виді:

 

Z_imax=max[αx_i+β (К_i – x_і] - r[αхі+β(К_i-x_i)],

 

де r - коефіцієнт, який характеризує частину прибутку, що вкладається

розвиток виробництва.

Основне функціональне рівняння при цьому приймає вид:

Z_imax=max[αx_i+β (К_i – x_і) - r[αхі+β(К_i-x_i))+Z_(i+1)max].

при 0≤ x_i ≤ К_i.

 

В подальшому процедура рішення залишається незмінною.

Якщо розглядається задача розподілу ресурсів між п об'єктами господарської діяльності, то приходиться на кожнім кроці мати п оптимальних рішень (але не 2, як ми розглядали). Тоді u_i =(x_i⁽¹⁾, x_i⁽²⁾…… x_i⁽ⁿ⁾) – вектор вкладень в підприємства на початок і-го року.

Процес пошуку оптимальної стратегії управління вкладеннями на кожному кроці також зважується поетапно. Стан системи перед початком кожного етапу як і раніше буде характеризуватися одним числом (К_i) (,m – число етапів). Складніше буде с вибором управлінь (капіталовкладень в к-е підприємство на кожному і-му етапі x_i^k).

Необхідно виконати наступні умови на i -му кроці:

 

 

При цьому основне функціональне рівняння матиме вид:

Це вже класична задача ЛП, розв'язання якої вже розглядалося у попередньому розділі, що має вирішуватися для кожного i -го кроку.

Досить часто в практиці приходиться вирішувати задачу розподілу ресурсів із вкладенням прибутку в розвиток виробництва. Подібні задачі називаються виродженими. Особливістю їх є те, що вони вирішуються з першого до останнього кроку, (тільки вперед), що значно спрощує процедуру рішення.

Наприклад, для закупівлі устаткування 2-х типів, виділена сума 20000грн.. Ефективність вкладення цих засобів в устаткування оцінюється тим прибутком, що одержить підприємство, використовуючи це устаткування.

Нехай для устаткування 1-го типу коефіцієнт ефективності (прибутку) складає α₁= 0,4; для 2-го типу α₂ =0,42. Наприкінці звітного періоду використане устаткування реалізується за ціною 0,7 і 0,6 первісної вартості (коефіцієнти амортизації відповідно β₁=0,7 і β₂=0,6). Отримані від продажу кошти, а також отриманий прибуток знову вкладаються в придбання устаткування 1-го і 2-го типів.

Ставиться задача знайти оптимальний розподіл коштів для їх ^купівлі протягом 3-х років.

Рішення

Складемо функціональну модель процесу (рис.7.3).

Рис.7.3 Модель процесу з вкладенням коштів у розвиток виробництва

Перший крок.

Знаючи початкове значення К₁, одержуємо для К₂:

 

К₂ = [ α₁х₁ + α ₂х₂ + β₁x₁ + β ₂x₂ ]

 

Враховуючи x₂=К₁ – х₁ запишемо:

 

К₂ = [ α₁х₁ + α₂(k₁ –х₁) + β₁x₁ +β₂ (К₁ –х₁)] =

= [(α₁ – α₂ + β₁ – β₂ )x₁ + (α ₂ + β₂)K₁]

K₂ буде максимальним при х₁ =K₁

 

Таким чином, стратегія управління на 1-му кроці: x₁=K₁; x₂=0. При

 

α₁ =0,4, α₂ =0,42; β₁ =0,7; β₂ =0,5:

 

Величина капіталовкладень на початок другого року K₂=1,1K₁.

Другий крок.

Аналізується аналогічно першому:

К₂ = [ α₁х₁ + α ₂х₂ + β₁x₁ + β ₂x₂ ] =

= [ (α₁ – α₂ + β₁ – β₂ )x₁ + (α ₂ + β₂)K₂ ]=

= max[ 0.08x₁ + 1.02K₂ ]=1,1 K₂= 1,12 K₁

при х₁ =К₁ і т.д..

Очевидно, що можливі варіанти закупівлі устаткування різного типу на кожен етап розвитку. У цьому випадку уточнюється значення α_i і β_i на кожному кроці.

Можливо також поєднання різних схем використання коштів. Пропонуємо читачам самим вирішити задачу за умови, що на 1-му етапі весь прибуток вкладається в придбання устаткування, а на наступному повністю відраховується як дивіденд від діяльності підприємства Необхідно максимізувати прибуток за останні 2 роки.