Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Імітаційне моделювання транспортних систем масового обслуговування
Імітаційне моделювання є дуже поширеними при аналізі функціонування транспортних систем масового обслуговування, коли потоки заявок не відповідають пуассонівському закону розподілу ймовірностей їх надходження до СМО. Це пояснюється тим, що теоретичні аспекти аналізу систем масового обслуговування (СМО) досить детально розглянуті в чисельних роботах [2,3,4,12]. Усі аналітичні методи базуються на аналізі графів стану систем (див. рис.9.4), ймовірності яких визначаються відомими диференційними рівняннями Колмогорова. У стислому вигляді ці питання були розглянуті також в даному посібнику в попередньому розділі.
Рис.9.4 Типовий граф станів СМО
Але аналітичні методи є добре розвинутими лише при умові існування саме пуассоновських вхідного та вихідного потоків систем. Для “непуассоновських” потоків існують лише формули Полячека - Хінчина для визначення середньої довжини черги СМО без відмов та універсальна формула Літтла для визначення середнього часу очікування заявки Тому імітаційне моделювання саме транспортних СМО має неабияку практичну Слід зауважити, що створювати й використовувати імітаційні моделі СМО доцільно лише тоді, коли випадкові фактори повністю описані з допомогою відповідних характеристик (імовірність, щільність розподілу ймовірностей тощо). Ці характеристики вивчаються на базі емпіричних даних, добраних або при систематизації наявних звітних матеріалів або в результаті обробки спеціально поставлених експериментів. Тому розробляючи імітаційну модель СМО, завжди стикаються з проблемою: чи доцільно в методі Монте-Карло застосовувати безпосередньо емпіричні дані? Можливо, є рація скористатися одним із апроксимуючих теоретичних розподілів. Питання про використання емпіричних або теоретичних розподілів дуже важливе, і ось чому. 1. Коли використовують «сирі» емпіричні дані, мають на увазі що моделюється лише минуле. Дані, здобуті раніше, строго кажучи відбивають лише колишню поведінку системи; можливими подіями виявляються тільки ті, які вже відбувалися. Звідси випливає необхідність припустити, що основна форма розподілу імовірності лишиться з часом без змін і що особливості цього розподілу, які стосуються певного періоду часу, будуть повторюватися.
2. Завдяки застосуванню теоретичного розподілу здебільшого вдається зменшити витрати машинного часу і потрібної пам'яті ЕОМ Але якщо з допомогою аналізу функціонування системи не вдається дібрати адекватну модель, котра узгоджується на статистично прийнятному рівні надійності з експериментальними даними, то слід скористатися саме імітаційною моделлю СМО. Покажемо принцип побудови імітаційної моделі СМО.
Припустимо для простоти, що в початковий момент (t = 0) система знаходиться в стані S0 (вільна)(див. рис.9.4). Почнемо моделювання з того, що розіграємо на осі ot потік заявок, тобто ряд випадкових точок t1, t2, t3, - моментів надходження відповідних заявок— першої, другої і т. п. (рис 9 5). Рис. 9.5 Графічне зображення вхідного потоку
Розіграш потоку заявок проводиться наступним чином. Будується визначена на етапі попереднього обстеження вхідного потоку функція розподілу випадкової величини Т— інтервалу між заявками, що надходять в СМО:
і розігрується значення випадкової величини Т1, як це описано вище. Відстань Ті відкладається від початку координат; при цьому отримуємо момент t1 надходження першої заявки. Потім процедура розіграшу повторюється і нове значення Т2 відкладається від t1 отримуємо момент t2 надходження другої заявки, і т. д. Таким чином ми будуємо ланцюг моментів надходження заявок, зображений на рис.9.5. Зрозуміло, цей ланцюг необхідно зробити достатньо довгим, розігравши, в усякому разі, не менше декількох сотень значень випадкової величини Т. В якості прикладу розглянемо принцип функціонування імітаційної моделі двоканальної СМО з чергою очікування, що обмежена трьома заявками. Зобразимо процедуру моделювання за допомогою наглядної схеми (рис. 9.6).
Рис.9.6 Графічне зображення функціонування СМО
Зверху помістимо ось часу (0) з відміченими на ній моментами надходження заявок. Нижче неї помістимо ще п'ять висей: (1), (2), (3), (4), (5). На осях (1) і (2) ми будемо зображувати стани першого і другого каналів (жирна лінія — «зайнятий», тонка — «вільний»). На осях (3), (4), (5) ми будемо зображувати стани першого, другого і третього місць в черзі (жирна лінія — «зайнято», тонкої— «вільне»). Всі п'ять осей мають той же відлік часу, що й ось (0).
До моменту t1 — надходження першої заявки — всі канали і всі місцяв черзі вільні. В момент t1 надходить перша заявка й займає перший канал.Скільки часу він буде зайнятий — вирішується розіграшем поточногоінтервалу часу обслуговування, що також моделюється за зазначеною раніше схемою генерування потоку з визначеною щільністю розподілу. Перше розігране значення часу обслуговування τ позначимо τ1 і відкладемо на осі (1) от точки з абсцисою t1 відмічаючи його жирною лінією (рис.9.6). В момент надходження другої заявки t2 перший канал ще зайнятий; заявка займає другий канал. Розіграємо ще одне значення τ позначимо τ 2 і відкладемо його жирною лінією на осі (2) від точки с абсцисою t2. Заявка t3, яка надійшла в момент, коли обидва канали зайняті, стає в чергу, займає на ній перше місце (вісь (3)) і очікує до того моменту, коли звільниться один з каналів. В нашому випадку раніше звільняється канал (2) — в цей момент заявка з вісі (3) перескакує на вісь (2) — і знову розігрується час обслуговування τ 3 цієї заявки. На вісі (2) будується нова жирна ділянка, а вісь (3) продовжується тонкою лінією — місце в черзі вільне. На цьому рисунку проти кожної ділянки зайнятості каналу (місця в черзі) для зручності обробки проставлений номер заявки, яка займає це місце; можна прослідкувати, як заявка «мандрує» з останніх місць в черзі на перші, потім — на обслуговування. Заявка, яка отримала відмову, відмічається зірочкою (юна залишає СМО без обслуговування). Припустимо, що моделювання реалізації продовжено нами достатньо довго (настільки довго, що вплив початкових умов вже перестає діяти).Тоді стає можливим визначити ймовірнісні характеристики роботи СМО. Ймовірність р0, p1, р2 того, що будуть зайняті 0, 1, 2 канали, знайдемо наступним чином. Розділимо всю ось 0t на ділянки, які відповідають кількості зайнятих каналів. Ділянки часу, на яких не зайнятий ні один канал, відмітимо цифрою 0, один канал — цифрою 1, два каналу — цифрою 2. На більшій ділянці часу Т додамо довжини всіх ділянок, помічених нулем — отримуємо Т0; сума довжин всіх дільниць, помічених одиницею, буде Т1, двійкою — Т2. Очевидно, що завжди має місце рівність
Т0+ Т1+Т2=Т.
При більшому Т імовірності р0, p1, р2 будуть приблизно дорівнювати відношенням відповідного часу до загальному часу, тобто:
Відмітимо, що ділянку Т доцільно підраховувати не з самого початку процесу, де ще здійснюється вплив початкових умов, а від більш віддаленого по часу моменту 0', де вплив початкових умов вже практично перестає діяти. Знайдемо імовірності р0, p1, р2та. р3того, що в черзі будуть стояти 0, 1, 2, 3 заявки. Знову розіб'ємо велику ділянку осі часу Т на частини, помічені 0, 1, 2, 3, на яких в черзі знаходиться відповідно 0, 1, 2, 3 заявки. Додавши довжини всіх однаково помічених дільниць і поділивши суми Ті на Т, отримуємо:
Середню кількість зайнятих каналів z отримуємо звичайним способом як математичне очікування дискретної випадкової величини Z — кількості зайнятих каналів:
Середній час очікування заявки в черзі tоч знаходимо наступним чином: розглянемо ряд заявок, які надійшли протягом великого проміжку часу Т в моменти
tK, tk1,..., tk+i,.., tk+N
і для кожної з них безпосередньо підрахуємо час очікування в черзі
Якщо нас цікавить не просто середній час очікування, а умовний середній час, обчислений при умові, що заявка була прийнята до обслуговування, то середнє арифметичне часу очікування обчислюється не для всіх заявок, а тільки для тих, які були обслужені. Дисперсія часу очікування знаходиться аналогічним чином, як середнє арифметичне квадратів часу очікування мінус квадрат середнього часу очікування:
Ймовірність відмови на великій дільниці часу Т - це відношення кількості заявок N*, помічених зірочкою (які отримали відмову), до загальної кількості N заявок, які надійшли за цей час:
На завершення цього розділу приведемо алгоритм імітаційного моделювання n - канальної СМО (рис.9.7), де Тk- поточний час моделювання; Ткон – заданий період моделювання; j – поточний номер заявки, що надійшла в СМО, і – поточна кількість зайнятих каналів обслуговування. Решта у схемі не потребує пояснень.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.161.222 (0.02 с.) |


 (9.15)
(9.15)
 (9.16)
(9.16)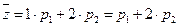 (9.18)
(9.18) , який дорівнює нулю, якщо (к+i)-а заявка була зразу прийнята до обслуговування (або отримала відмову), і суми часу очікування цієї заявки на різних осях ((3), (4) і (5)), якщо вона стояла в черзі. Середній час очікування заявки в черзі приблизно знаходиться як середнє арифметичне цих часів:
, який дорівнює нулю, якщо (к+i)-а заявка була зразу прийнята до обслуговування (або отримала відмову), і суми часу очікування цієї заявки на різних осях ((3), (4) і (5)), якщо вона стояла в черзі. Середній час очікування заявки в черзі приблизно знаходиться як середнє арифметичне цих часів: (9.19)
(9.19) (9.20)
(9.20)  (9.21)
(9.21)