
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные системы дифф.ур.Содержание книги
Поиск на нашем сайте
Линейной однородной системой наз. Нормальная линейная система д.у. вида Решениями данной системы будут некоторые вектор-функции с компонентами определёнными на [α;β]. Непосредственным образом проверяются следующие утверждение наз. принципом суперпозиции для системы (1). Лемма 1: Если у1 и у2 есть решение системы (1), а С1 и С2-произвольные числа, то вектор функция у=С1у1+С2у2, также будет решением исходной системы (1). Опр.1:Вектор-функции у1,…,ук наз. линейно зависимыми на промежутке I, если найдутся такие числа С1,…,Ск одновременно не равные нулю, что имеет место тождество С1у1+…+Скук=0, в противном случае данные вектор-функции наз. линейно независимыми на промежутке I. Лемма 2: Если вектор-функции Обратное утверждение вообще говоря неверно. Т.1: Пусть Следствие 1: Решения Опр.2:Любая система n линейно независимых решений системы (1.27) на [α;β] назыв.фундаментальной системой решений(ФСР) этой системы. Т. 2: Для системы (1) существует бесконечное множество ФСР. Т.3: Если Рассмотрим начальные условия Решение y каждой задачи Коши (1), (2) однозначно определяется с помощью вектор-функции (3)- общее решение системы (1). Опр.3: Матрицу Ф(x) у которой столбцы образуют ФСР Тогда общее решение (1) y(x)=Ф(x) C. Рассмотрим на [α;β] матричные дифф.ур. Пусть
Имеем, что произвольная фунд.матрица системы (1) имеет представление Решение матричного дифф.ур.(4) с начальными условиями Матрица Опр.4: Определителем Вронского системы вектор-функций
Т.4: Решение Т.5: Решение Т.6: Пусть W(x) есть Вронскиан решений
|
|||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.176 (0.009 с.) |

 =A(x)y (1), где А(х)-заданная непрерывная на [α;β] квадратная матрица порядка n,(а в некоторых случаях комплекснозначная).
=A(x)y (1), где А(х)-заданная непрерывная на [α;β] квадратная матрица порядка n,(а в некоторых случаях комплекснозначная). j=1,..,k линейно зависимы на промежутке I, то при всех
j=1,..,k линейно зависимы на промежутке I, то при всех  ϵ I числовые векторы
ϵ I числовые векторы  (
( линейно зависимы числовые векторы
линейно зависимы числовые векторы  есть ФСР системы (1), то каждое решение y этой системы единственным образом представимо в виде
есть ФСР системы (1), то каждое решение y этой системы единственным образом представимо в виде 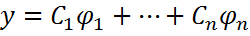 , где
, где  -некоторые числа.
-некоторые числа.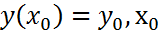 ϵ [α;β] (2).
ϵ [α;β] (2). (3), где
(3), где  (4) с неизвестной квадратной матрицей Y(x).
(4) с неизвестной квадратной матрицей Y(x). . Отсюда видно, что матрица
. Отсюда видно, что матрица  тогда и только тогда будет решением ур. (4), когда её вектор-столбцы
тогда и только тогда будет решением ур. (4), когда её вектор-столбцы  являются решениями системы (1). Значит фундаментальная матрица Ф(x) является решением уравнения (4). В силу не вырожденности фунд.матрицы получаем, что общее решение ФСР
являются решениями системы (1). Значит фундаментальная матрица Ф(x) является решением уравнения (4). В силу не вырожденности фунд.матрицы получаем, что общее решение ФСР 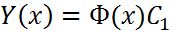 , где С- произвольная квадратная матрица порядка n.
, где С- произвольная квадратная матрица порядка n. .
. где I – единичная матрица назыв. матрицантом системы (4).
где I – единичная матрица назыв. матрицантом системы (4). является матрицантом дифф.системы (1).
является матрицантом дифф.системы (1). .
. системы (1) линейно зависимы на [α;β] тогда и только тогда, когда на этом отрезке имеет место тождество
системы (1) линейно зависимы на [α;β] тогда и только тогда, когда на этом отрезке имеет место тождество 
 (5), где
(5), где - след матрицы A(x).
- след матрицы A(x).


