
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные дифференциальные уравнения n порядка с постоянными коэффициентами.
Рассмотрим линейное однородное д.у. n порядка с постоянными коэффициентами Рассмотрим сначала случай, когда все корни 4.25 веще-ые и различные. Им соответ. n- решений Непосредственным вычислениям убеждаемся, что данные фун-ии образуют фунд. Си-му решений ура-ия 1.25. Тогда общее решение исходного ура-ия 1.25 имеет вид Пусть все корни харак. Ура-ия различны, но среди них есть комплексные. Тогда с учетом того, что коэфф-ты хар. ура-ия вещественны, приходим к выводу, что комплексные корни входят парами вида:
Так как частная Рассмотрим теперь случай кратных корней хар. ур-ия. Непосредственными вычислениями на основании мат. индукции можно получить формулу сдвига
В частности, когда многочлен L(p) представляет собой степень
Рассмотрим сначало случай, когда λ есть веще-ый корень кратности k хар. ура-ия. Тогда имеет место цепочка соотношений:
Покажем, что ему соответствует ровно k линейно независимых решений.
Подставим данный k-решений в ура-ие 2.25 и применим формулу сдвига 11.25. В результате получаем соотношение
Где Полагая, что в полученной формуле р=0 получаем, что Далее последовательно дифференцируя по р соотношение 14.25 и полагая, получим соотношение р=0, получаем след. формулы
Тогда, на основании формулы 14.25 получаем, что
В итоге, из соотношения 13.25 получаем, что Это означает, что фу-ия
|
|||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.213.214 (0.008 с.) |
 (1.25). Здесь
(1.25). Здесь  , ј=
, ј=  есть вещественные числа. Введем символический оператор
есть вещественные числа. Введем символический оператор  , который обозначает дифференцирование по переменной x. При этом представим производные
, который обозначает дифференцирование по переменной x. При этом представим производные  как степени оператора
как степени оператора  . Будем считать, что при ј=0 степень данного оператора равна самой фу-ии (1.25). Левую часть можно записать в виде
. Будем считать, что при ј=0 степень данного оператора равна самой фу-ии (1.25). Левую часть можно записать в виде  +…+
+…+ 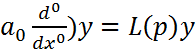 , где
, где  =
=  . Очевидно, что
. Очевидно, что  (2.25). Будем искать частные решения д.у. 1. 25. В виде
(2.25). Будем искать частные решения д.у. 1. 25. В виде 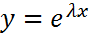 (3.25). Подставляя фу-ию 3.25. получаем, что
(3.25). Подставляя фу-ию 3.25. получаем, что  =
=  =0. Отсюда видно, что λ является корнем алгебраического ура-ия
=0. Отсюда видно, что λ является корнем алгебраического ура-ия  (4.25), то фу-ия 3.25 есть решение д.у. 1.25
(4.25), то фу-ия 3.25 есть решение д.у. 1.25 ,
, 
 +…+
+…+ 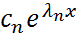 (5.25), где
(5.25), где  – есть произвольная постоянная.
– есть произвольная постоянная. ,
,  . Для комплексного корня
. Для комплексного корня  ,комплексно значную фу-ию вещественного аргумента
,комплексно значную фу-ию вещественного аргумента  (6.25). Непосредственной проверкой убеждается, что данная фу-ия является решением ур-ия (1.25). Аналогичным образом приходим к выводу, что фу-ия
(6.25). Непосредственной проверкой убеждается, что данная фу-ия является решением ур-ия (1.25). Аналогичным образом приходим к выводу, что фу-ия  =
=  (7.25) также является решением ур-ия (1.25). Решение однородного ур-ия (1.25) обладают свойством линейности, поэтому вещественные фу-ии
(7.25) также является решением ур-ия (1.25). Решение однородного ур-ия (1.25) обладают свойством линейности, поэтому вещественные фу-ии , (9.25)
, (9.25)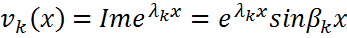
 , то данное решение является линейно-незав. Таким образом мы получили m-пар комплексно-сопряженных корней
, то данное решение является линейно-незав. Таким образом мы получили m-пар комплексно-сопряженных корней 
 ,
,  хар. ур-ия 4.25 и n-2m различных вещественных корней
хар. ур-ия 4.25 и n-2m различных вещественных корней  ,
,  данного хар. ур-ия. Таким образом лбщее решение исходного ур-ия имеет вид
данного хар. ур-ия. Таким образом лбщее решение исходного ур-ия имеет вид  (10.25)
(10.25) (11.25).
(11.25). :
: (12.25)
(12.25)

 (13.25)
(13.25) (14.25).
(14.25).
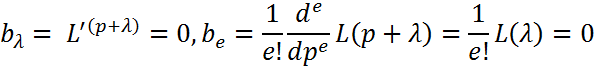
 . Так как r<k отсюда следует
. Так как r<k отсюда следует 

 кратности
кратности  линейно независимых частных решений исходного д.у. и при этом
линейно независимых частных решений исходного д.у. и при этом 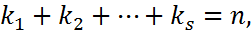 таким образом мы получаем на основании данных корня равно n-функций, образующих фундаментальную си-му решений ура-ия 2.25. Поэтому в данном случае общее решение исходног д.у. имеет вид.
таким образом мы получаем на основании данных корня равно n-функций, образующих фундаментальную си-му решений ура-ия 2.25. Поэтому в данном случае общее решение исходног д.у. имеет вид. + …+
+ …+  .
.


