
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные системы с периодическими коэффициентами.
Рассмотрим систему Такие матричные функции – периодическими с периодом Теорема 1.31. Каждую фундаментальную матрицу системы (1.31) можно представить в виде Ф(t)=G(t)etR(2.31),где G(t)- Матрица В определенная формулой Ф(t+ Пусть Ф1(t) есть какая-либо другая фундаментальная матрица системы(1.31). На ее основе определяем другую матрицу монограммии в виде Ф1(t+ Кроме того учтем связь между двумя фундаментальными матрицами системы (1.31) в виде Ф1(t)=Ф(t)*S, dtS Сравнивая последнее соотношение (3.31) получаем, что В=SB1S-1, где S-1- матрица обратная к матрице S, таким образом мы получим, что все матрицы монограммии системы(1.31) подобны между собой. Отметим, что иногда матрицу монограммии – матрицу, которая определяется нормированной при t Рассмотрим собственные числа Кроме того собственные числа Из определения постоянной матрицы R имеем, что Отметим также, что характеристические показатели определены с точностью до слагаемого На основание формулы (4.31) и формулы Лиувиля - Остроградского получаем, что определитель матрицы В: detВ=exp На основание последнего соотношения получаем, что
Заметим, что название мультипликатор(множитель) объясняется следующим утверждением. Теорема2.31. Число Следствие 1.31. Для того чтобы система (1.31) имела хотя бы одно нетривиальное
Из формулы (2.31) вытекает, что фундаментальная матрица система (1.31)представляет собой произведение не особой матрицы G(t) на фундаментальную матрицу Подставляя последнее выражение в формулу (9.31) получаем систему Таким образом мы получаем следующее утверждение. Теорема3.31. Существует линейная замена переменных (8.31), где G(t) Данное свойство системы (1.31)- приводимостью.
|
|||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.139.50 (0.004 с.) |
 где вещественная матричная функция Р удовлетворяет следующему условию
где вещественная матричная функция Р удовлетворяет следующему условию 
 или
или  Результаты, которые мы получим в этом параграфе образуют основу теории Флоке-Ляпунова.
Результаты, которые мы получим в этом параграфе образуют основу теории Флоке-Ляпунова. -периодическая матрица для
-периодическая матрица для  , R- постоянная матрица.
, R- постоянная матрица.
 ,
,  .
.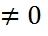 фундаментальной матрицей Ф(t) системы(1.31)
фундаментальной матрицей Ф(t) системы(1.31)  (0)=
(0)=  . Тогда на основании соотношения (3.31) получаем, что В=
. Тогда на основании соотношения (3.31) получаем, что В=  (
(
 матрицы монограммии, они называются мультипликаторами системы(1.31).
матрицы монограммии, они называются мультипликаторами системы(1.31). постоянной матрицы R из теоремы 1.31 называются характеристическими показателями системы(1.31).
постоянной матрицы R из теоремы 1.31 называются характеристическими показателями системы(1.31).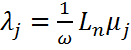 , j=
, j= 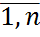 .При этом простым мультипликатором соответствуют простые характеристические показатели, а кратным мультипликатором соответствуют характеристические показатели с элементарными делителями той же кратности.
.При этом простым мультипликатором соответствуют простые характеристические показатели, а кратным мультипликатором соответствуют характеристические показатели с элементарными делителями той же кратности.
 .
. (5.31).
(5.31).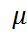 является мультипликатором системы(1.31) тогда и только тогда, когда существует ненулевое решение
является мультипликатором системы(1.31) тогда и только тогда, когда существует ненулевое решение  этой системы такое, что
этой системы такое, что  .
. периодическое решение необходимо и достаточно, чтобы хотя бы один из его мультипликаторов был равен 1.
периодическое решение необходимо и достаточно, чтобы хотя бы один из его мультипликаторов был равен 1. с постоянными коэффициентами. Поэтому можно ожидать, что преобразование X=G(t)*y (8.31) переводит систему (1.31) в систему (8.31).В самом деле на основании формулы(8.31) получаем
с постоянными коэффициентами. Поэтому можно ожидать, что преобразование X=G(t)*y (8.31) переводит систему (1.31) в систему (8.31).В самом деле на основании формулы(8.31) получаем  (9.31). Так как G=Ф(t)*e-tR,то получаем
(9.31). Так как G=Ф(t)*e-tR,то получаем 
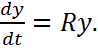
 есть не особая гладкая
есть не особая гладкая 


