
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квазилинейное уравнение в частных производных 1-го порядка.Содержание книги
Поиск на нашем сайте Опр.5,20 Квазилинейным диф. уравнением 1-го порядка с частными производными будем называть уравнение где
Процесс нахождения общего решения д.у. (14.20) аналогичен нахождению общего решения неоднородного д.у. 1.20. Сначала строим систему уравнений характеристик в виде:
Интегральные кривые этой системы называют характеристиками квазилинейного д.у (14.20), если в области G найдены n независимых первых интегралах Постановка задачи Коши для квазилинейного уравнения (14.20) аналогично постановке этой задачи для однородного уравнения Пусть решение Сначала находим первые интегралы Переменные В соотношении (17.20) подставляем выражение В результате получаем решение исходного уравнения в неявном виде
Уравнение Пфаффа. Уравнение Пфаффа (П) представляет собой обобщение д.у.первого порядка в симметрической форме и в трехмерном случае имеет вид P(x,y,z)dx+Q(х,у,z)dу+R(х,у,z)dz=0 (1),где Р,Q,R есть некоторые функции, гладкие по своим аргументам в области G Интегралом уравнения П(1) будем наз.такую зависимость переменных х,у,z при которой дифференциалы dx,dy,dz обращают уравнение (1) в тождество на области G.Если указанная зависимость представима в виде: u(х,у,z)=0 (или в параметрическом виде х =х(u,v),у=у(u,v),z=z(u,v)),то ее будем наз. двумерным интегралом или интегральной поверхностью ур.П(1). Если же интеграл ур. П представим в виде: u(х,у,z)=0,v(х,у,z)=0 (или в параметрическом виде х=х(t),у=у(t),z=z(t)),то такую зависимость между переменными х,у,z будем наз. одномерным интегралом или интегральной кривой(1). Рассмотрим в пр-ве Охуz векторное поле (P(x,y,z),Q(х,у,z), R(х,у,z))= Т.1. Условие rоt В координатной форме ур.П имеет вид: P(
|
||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |

 ,
, и
и  есть функции гладкие в некоторой области
есть функции гладкие в некоторой области  из
из  .
.
 , то все решения д.у. (14.20) можно получить из формулы
, то все решения д.у. (14.20) можно получить из формулы  (13).
(13). , при практическом решении задачи Коши будем использовать следующий алгоритм
, при практическом решении задачи Коши будем использовать следующий алгоритм д.у (14.20) удовлетворяет условию
д.у (14.20) удовлетворяет условию 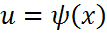 на поверхности S заданным уравнением
на поверхности S заданным уравнением  .
. системы уравнений характеристик (15.20) при этом мы рассматриваем интегралы независимые в области G. Далее исключаем из системы уравнений
системы уравнений характеристик (15.20) при этом мы рассматриваем интегралы независимые в области G. Далее исключаем из системы уравнений 
 ,u. В результате получаем равенство вида
,u. В результате получаем равенство вида 

 .
. .
.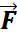 (х,у,z). Если двумерный или одномерный интеграл ур.(1) задан векторным ур.:
(х,у,z). Если двумерный или одномерный интеграл ур.(1) задан векторным ур.:  =
=  +у
+у  +z
+z 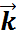 ,то имеет место соотношение: d
,то имеет место соотношение: d  +
+  +
+  . Здесь dx,dy,dz в силу определения интеграла ур.П вычислены с учетом существующей зависимости между переменными х,у,z.Поэтому ур.П(1) можно записать в следующей векторной форме:
. Здесь dx,dy,dz в силу определения интеграла ур.П вычислены с учетом существующей зависимости между переменными х,у,z.Поэтому ур.П(1) можно записать в следующей векторной форме:  d
d  , данное векторное поле будем наз.ротором векторного поля
, данное векторное поле будем наз.ротором векторного поля 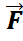
 =0,
=0,  (х,у,z)
(х,у,z)  G(3) является необходимым для существования двумерных интегралов ур.П(1) в области G.
G(3) является необходимым для существования двумерных интегралов ур.П(1) в области G. -
-  )+Q(
)+Q( 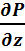 -
-  )+R(
)+R(  -
- 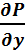 )=0(4).
)=0(4).


