Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные уравнения в частных производных 1-го порядка.Стр 1 из 7Следующая ⇒
Линейные однородные уравнения в частных производных 1-го порядка. Опр.1: Линейным неоднородным дифф. ур. 1-го порядка с частными производными будем назыв. уравнение вида
Где Опр.2: При
Опр.3: Решением дифф.ур-й (1) и (2) в области D будем назыв.гладкую в области D функцию, которая обращает это уравнение в равенство в каждой точке Подставим в соответствие однородному уравнению (2) систему обыкновенных дифф.ур-й:
Так как
Опр.4: Систему (3) будем назыв.системой уравнений характеристик для однородного дифф.ур. (2), а её фазовые траектории – характеристикой.
Т.1:Функция
Квазилинейное уравнение в частных производных 1-го порядка. Опр.5,20 Квазилинейным диф. уравнением 1-го порядка с частными производными будем называть уравнение где
Процесс нахождения общего решения д.у. (14.20) аналогичен нахождению общего решения неоднородного д.у. 1.20. Сначала строим систему уравнений характеристик в виде:
Интегральные кривые этой системы называют характеристиками квазилинейного д.у (14.20), если в области G найдены n независимых первых интегралах Постановка задачи Коши для квазилинейного уравнения (14.20) аналогично постановке этой задачи для однородного уравнения Пусть решение Сначала находим первые интегралы Переменные В соотношении (17.20) подставляем выражение В результате получаем решение исходного уравнения в неявном виде
Уравнение Пфаффа.
Уравнение Пфаффа (П) представляет собой обобщение д.у.первого порядка в симметрической форме и в трехмерном случае имеет вид P(x,y,z)dx+Q(х,у,z)dу+R(х,у,z)dz=0 (1),где Р,Q,R есть некоторые функции, гладкие по своим аргументам в области G Интегралом уравнения П(1) будем наз.такую зависимость переменных х,у,z при которой дифференциалы dx,dy,dz обращают уравнение (1) в тождество на области G.Если указанная зависимость представима в виде: u(х,у,z)=0 (или в параметрическом виде х =х(u,v),у=у(u,v),z=z(u,v)),то ее будем наз. двумерным интегралом или интегральной поверхностью ур.П(1). Если же интеграл ур. П представим в виде: u(х,у,z)=0,v(х,у,z)=0 (или в параметрическом виде х=х(t),у=у(t),z=z(t)),то такую зависимость между переменными х,у,z будем наз. одномерным интегралом или интегральной кривой(1). Рассмотрим в пр-ве Охуz векторное поле (P(x,y,z),Q(х,у,z), R(х,у,z))= Т.1. Условие rоt В координатной форме ур.П имеет вид: P( Метод функции Ляпунова. Рассмотрим нормальную обыкновенную систему ДУ (1)
Пусть Теорема1. (теор. Ляпунова об устойчивости) Если сущ. Функция v для которой выполняются соотношения: То нулевое решение системы (1) устойчиво. Функция удовлетворяющее условию (2) наз. функциями Ляпунова Следствие1. Если система (1) имеет автономный (стационарный, независящий от времени Теорема2 (теор. Ляпунова об асимптотический устойчивости)Если сущ. ф-ий v и w такие, что выполняются соотношения То нулевое решение системы (1) асимптотический устойчиво. Теорема3. (теор. Ляпунова о неустойчивости) Если сущ. ф-ий v и w такие,что Систему (1) вида При этом автономную линейную систему Теор4. (об устойчивости) Если линеаризация (6) асимптотически устойчива, то асимптотически устойчива и нулевое решение квазилинейной системы (5) Следствие 2 Если вектор-ф-ия f(x) непрерывно диф-ма в окрестности т. х=0, где все характеристические числа матрицы Якоби Теор5 (о неустойчивости) Если хотя бы одно характеристическое число матрицы А имеет положительную действительную часть, то нулевое решение квазилинейной системы (5) не устойчиво.
Автономные системы. Рассмотрим автономную систему Тогда при начальном условии Это решение рассматривается как закон движения точки в пространстве При этом точка x описывает некоторую траекторию При законе движения x=x(t) вектор скорости определяется по формуле Специфика автономной системы (1) у которой в правую часть не входит время t состоит в том, что заданное поле скоростей не меняется с течением времени, т.е. является стационарным. При продолжении решения 1) решение может быть продолжено на всю полуось 2)при приближении Далее будем считать, что всегда имеет место первая ситуация. Покажем, что это ограничение не уменьшает общности. В самом деле вместе с системой (1) рассмотрим автономную систему
Поэтому можно подобрать скалярную функцию r так, чтобы скорость движения определяемая системой (2) была ограниченной. В этом случае движущаяся точка не может уйти в бесконечность за конечное время, т.е.2-ая ситуация не возможна.
Для каждой точки Вектор-функция (3) обладает следующими свойствами: 1) она непрерывна по совокупности переменных; 2) 3) Из свойства 2),3) вытекает, что при фиксированных параметрах t отображение Свойство: Если две траектории имеют общую точку, то они совпадают, а соответствующие решения отличаются лишь сдвигом по времени. Т.1: Решение x(t) системы (1) может быть только одного из следующих трёх видов: 1) непериодическое, для которого 2)периодическое для которого найдется такая постоянная T 3) постоянное, для которого Траектории соответствующие 1-му виду назыв. незамкнутыми; 2- замкнутыми; 3- точкой покоя или состоянием равновесия.
Интегрирующий множитель Рассмотрим ур-ние Опр.1: Непрерывно диффер. и не обращающийся в ноль на области G будем назыв. интегрирующим множителем ур-ния (1), если на обл. G ур-ние На основании его получаем диф. ур-ние частных производных для определ. ф-ции
Решение данного диф-ного ур-ния не проще, чем решение исходного диф-ного ур-ния (1). Отметим, что нас интересует лишь какое-либо решение ур-ния (1). На практике данное решение можно найти из каких-либо особенностей инт-щего множителя. Чаще всего его ищут либо В некотором случае решение диф. ур-ний вида (1) можно применять метод выделения полных диф. используя известные ф-лы: Если в диф-ном ур-нии (1) можно выделить полный диф-ал в некоторой ф-ции Линейные однородные уравнения в частных производных 1-го порядка. Опр.1: Линейным неоднородным дифф. ур. 1-го порядка с частными производными будем назыв. уравнение вида
Где Опр.2: При
Опр.3: Решением дифф.ур-й (1) и (2) в области D будем назыв.гладкую в области D функцию, которая обращает это уравнение в равенство в каждой точке Подставим в соответствие однородному уравнению (2) систему обыкновенных дифф.ур-й:
Так как
Опр.4: Систему (3) будем назыв.системой уравнений характеристик для однородного дифф.ур. (2), а её фазовые траектории – характеристикой.
Т.1:Функция
|
||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.140.108 (0.041 с.) |
 , (1)
, (1) , b – есть заданные гладкие функции n переменных
, b – есть заданные гладкие функции n переменных  в области
в области  , u – искомая функция.
, u – искомая функция. в области G уравнение (1) назыв. линейным однородным дифф.ур. 1-го порядка с частными производными:
в области G уравнение (1) назыв. линейным однородным дифф.ур. 1-го порядка с частными производными: 
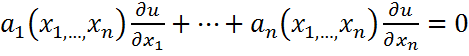 (2).
(2). .
. (3).
(3). , то систему (3) можно представить в симметрической форме:
, то систему (3) можно представить в симметрической форме: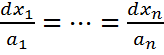 (4)
(4)
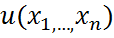 является решением однородной системы (2) в области D тогда и только тогда, когда она есть первый интеграл системы характеристик (3).
является решением однородной системы (2) в области D тогда и только тогда, когда она есть первый интеграл системы характеристик (3). ,
, есть функции гладкие в некоторой области
есть функции гладкие в некоторой области  из
из  .
.
 , то все решения д.у. (14.20) можно получить из формулы
, то все решения д.у. (14.20) можно получить из формулы  (13).
(13). , при практическом решении задачи Коши будем использовать следующий алгоритм
, при практическом решении задачи Коши будем использовать следующий алгоритм д.у (14.20) удовлетворяет условию
д.у (14.20) удовлетворяет условию 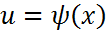 на поверхности S заданным уравнением
на поверхности S заданным уравнением  .
. системы уравнений характеристик (15.20) при этом мы рассматриваем интегралы независимые в области G. Далее исключаем из системы уравнений
системы уравнений характеристик (15.20) при этом мы рассматриваем интегралы независимые в области G. Далее исключаем из системы уравнений 
 ,u. В результате получаем равенство вида
,u. В результате получаем равенство вида 

 .
. .
.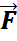 (х,у,z). Если двумерный или одномерный интеграл ур.(1) задан векторным ур.:
(х,у,z). Если двумерный или одномерный интеграл ур.(1) задан векторным ур.:  =
=  +у
+у  +z
+z 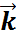 ,то имеет место соотношение: d
,то имеет место соотношение: d  +
+  +
+  . Здесь dx,dy,dz в силу определения интеграла ур.П вычислены с учетом существующей зависимости между переменными х,у,z.Поэтому ур.П(1) можно записать в следующей векторной форме:
. Здесь dx,dy,dz в силу определения интеграла ур.П вычислены с учетом существующей зависимости между переменными х,у,z.Поэтому ур.П(1) можно записать в следующей векторной форме:  d
d  , данное векторное поле будем наз.ротором векторного поля
, данное векторное поле будем наз.ротором векторного поля 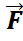
 =0,
=0,  (х,у,z)
(х,у,z)  G(3) является необходимым для существования двумерных интегралов ур.П(1) в области G.
G(3) является необходимым для существования двумерных интегралов ур.П(1) в области G. -
-  )+Q(
)+Q( 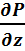 -
-  )+R(
)+R(  -
- 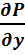 )=0(4).
)=0(4).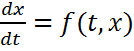 С непрерывной правой частью, определенной при
С непрерывной правой частью, определенной при  Кроме того будем считать, что система (1)имеет нулевое решение x
Кроме того будем считать, что система (1)имеет нулевое решение x 
 есть непрерывно дифференцируемые скалярные функции, положительные при х
есть непрерывно дифференцируемые скалярные функции, положительные при х  и обращаются в ноль при х=0.
и обращаются в ноль при х=0. (2)
(2) , певый интеграл v положительный в некоторой проколотой окрестности точки х=0 и v(0)=0 то нулевое решение системы (1) устойчиво.
, певый интеграл v положительный в некоторой проколотой окрестности точки х=0 и v(0)=0 то нулевое решение системы (1) устойчиво. ,
,  (3)
(3) ,
,  , будем наз. квазилинейной (системой с ведущей линейной частью) если равномерно при
, будем наз. квазилинейной (системой с ведущей линейной частью) если равномерно при 
 будем наз. линеаризацией системы (5) вдоль нулевого решения.
будем наз. линеаризацией системы (5) вдоль нулевого решения. имеют отрицательные действительные чисти, то нулевое решение автономной системы
имеют отрицательные действительные чисти, то нулевое решение автономной системы  асимптотически устойчиво.
асимптотически устойчиво.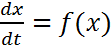 (1), где вектор-функция f(x) определена на всем пространстве
(1), где вектор-функция f(x) определена на всем пространстве  и удовлетворяет условию Липшица по всем своим аргументом в каждой ограниченной части пространства
и удовлетворяет условию Липшица по всем своим аргументом в каждой ограниченной части пространства  .
. существует и единственно решение
существует и единственно решение  системы (1) определенная в некоторой окрестности точки t=0.
системы (1) определенная в некоторой окрестности точки t=0. зависящая от выбора начальной точки
зависящая от выбора начальной точки  .
.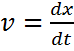 . Поэтому автономная система (1) задает поле скоростей (направлений) в фазовом пространстве
. Поэтому автономная система (1) задает поле скоростей (направлений) в фазовом пространстве  .
. вправо, т.е. в сторону возрастания t, возможны 2 ситуации:
вправо, т.е. в сторону возрастания t, возможны 2 ситуации: ;
; конечному t,
конечному t,  (т.е. решение уходит на бесконечность).
(т.е. решение уходит на бесконечность). (2), где скалярная функция
(2), где скалярная функция  и удовлетворяет тем же условиям, что и вектор-функция f(x). Эта система обладает теми же траекториями, что и система (1), отличается только скорости прохождения по эти траекториям.
и удовлетворяет тем же условиям, что и вектор-функция f(x). Эта система обладает теми же траекториями, что и система (1), отличается только скорости прохождения по эти траекториям.
 .
. пространства
пространства  при
при  ;
; (период), что
(период), что  ,а
,а  при
при  ;
;
 (1), где
(1), где 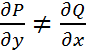 на области G.
на области G. явл. ур-нием полных диф-лов, если для ур-ния (1) существуетет интегр-щий множитель Q, то в силу
явл. ур-нием полных диф-лов, если для ур-ния (1) существуетет интегр-щий множитель Q, то в силу  он должен удолетв. соотношению:
он должен удолетв. соотношению: 
 :
: (2).
(2).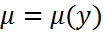 , либо
, либо  , тогда ур-ние (2) для нахождения ф-ции
, тогда ур-ние (2) для нахождения ф-ции 

 , то иногда данное уравнение можно упростить выполнив замену
, то иногда данное уравнение можно упростить выполнив замену  .
.