Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Чисельне диференціювання та інтегруванняСодержание книги Поиск на нашем сайте
Аналітичні методи диференціювання не завжди можна використати на практиці. Так, якщо функція задана як таблиця своїх значень, то, використовуючи аналітичні методи, не можна знайти ні похідної, ні інтеграла цієї функції. У багатьох випадках інтегрування функції, заданої за допомогою формули, або потребує значного об’єму роботи, або взагалі не можна виконати аналітично. В усіх цих випадках результат можна отримати за допомогою чисельних методів. Чисельне диференціювання. Нехай функція y (x) задана в рівновіддалених точках xk, k = 0, 1, …, n відрізка [ a, b ] за допомогою значень yk = f (xk). Для знаходження на відрізку [ a, b ] похідних
де u = (x – x 0): h; h = xk +1 – xk. Перемноживши біноми в чисельниках та врахувавши, що:
отримаємо:
Аналогічно можемо отримати:
Взагалі, так можна обчислити похідні будь-якого порядку. Щоб оцінити похибку обчислення похідних, необхідно взяти відповідну похідну від залишкового члена інтерполяційної формули Ньютона. Чисельне інтегрування. Нехай для функції y = f (x) необхідно обчислити інтеграл:
Вибором кроку h = (b – a): n розділимо відрізок [ a, b ] на n Замінюючи функцію y = f (x) відповідним інтерполяційним багаточленом Лагранжа Ln (x), отримаємо наближену квадратурну формулу:
де Нехай
u та w(u) були визначені при утворенні полінома Лагранжа. Тоді
Константи Hk називаються коефіцієнтами Котеса. Очевидні властивості Формула трапецій. Застосовуючи формулу (20), якщо n = 1, отримаємо:
Звідси: Це відома формула трапецій для наближеного обчислення визначеного інтеграла. Геометрично це означає, що площа криволінійної трапеції АА ¢ В ¢ В наближено дорівнює площі прямолінійної трапеції (рис. 10).
Рис. 10 Для обчислення інтеграла (19) проміжок інтегрування [ a, b ] ділимо на n рівних частин [ x 0; x 1], [ x 1; x 2], …, [ xn –1; xn ] і до кожного з них застосовуємо формулу трапецій. Припустимо, що h = (b – a): n, та позначимо yk = f (xk), k = 0, 1, …, n. Тоді можна записати:
звідки отримуємо загальну формулу трапецій:
Похибка формули (23):
Формула Сімпсона. З формули (21), якщо n = 2, знаходимо:
Звідки Отримана формула називається формулою Сімпсона. Наближене обчислення визначеного інтегралу за цією формулою геометрично означає заміну кривої у = f (х) параболою y = L 2(x), що проходить через три точки M 0(x 0, y 0), M 1(x 1; y 1) та M 2(x 2; y 2) (рис. 11).
Рис. 11 Для обчислення інтеграла (19) поділимо відрізок [ a, b ] на n = 2 m частин. Нехай yk = f (xk) — значення функції y = f (x) для рівновіддалених вузлів a = x 0, x 1, …, xn = b з кроком Застосовуючи формулу Сімпсона до кожного подвоєного проміжку довжиною 2 h, отримаємо:
Звідси маємо вираз загальної формули Сімпсона:
Похибка загальної формули Сімпсона визначається за формулою:
|
|||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.86.241 (0.009 с.) |



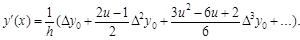

 (19)
(19) (20)
(20)
 (21)
(21) (22)
(22) та Hk = Hn–k.
та Hk = Hn–k.



 (23)
(23)