
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтегрування за допомогою степеневих рядів ⇐ ПредыдущаяСтр 5 из 5
Розглянемо визначений інтеграл (19). Нехай підінтегральна функція розкладається в степеневий ряд Застосовуючи теорему про почленне інтегрування степеневих рядів, інтеграл (19) можна подати у вигляді числового ряду:
Якщо ряд 24 збігається досить швидко, то можна приблизно обчислити визначений інтеграл за допомогою часткової суми ряду:
Похибка результату складається з похибки заміни ряду частковою сумою (наявність залишку ряду) та похибки округлення при обчисленні суми. Наближене розв’язання звичайних диференційних рівнянь (задача Коші) У багатьох галузях науки та техніки, зокрема в економічних науках, значна кількість задач зводиться до розв’язання диференційних рівнянь. Але кількість типів диференційних рівнянь, які можна розв’язати аналітично, дуже обмежена. Тому поряд з аналітичними та наближеними методами широко використовують чисельні методи розв’язання диференційних рівнянь, значимість яких особливо зросла у зв’язку з поширеним використанням ЕОМ. Нехай задане диференційне рівняння першого порядку розв’язане відносно похідної: y ¢ = f (x, y).(25) Будь-яка функція y = j(x), яка при підстановці в рівняння (25) перетворює його в тотожність, називається розв’язком цього рівняння. Загальний розв’язок рівняння (25) має вигляд y = j(x, С), де С — довільна константа. Геометрично загальний розв’язок є сімейством інтегральних кривих, тобто сукупністю ліній, що відповідають різним константам С. Задача Коші. Знайти розв’язок y = j(x) диференційного рівняння (25), що задовольняє початкову задану умову: y 0 = j(x 0). Геометрично задача Коші формулюється так: знайти інтегральну криву диференційного рівняння (25), яка проходить через задану точку М (x 0, y 0). Серед чисельних методів розв’язання задачі Коші найвідомішими є метод послідовних наближень, метод Ейлера та метод Рунге—Кута. Метод послідовних наближень полягає в тому, що розв’язок y (x) знаходять як границю послідовності функцій yn (x), які визначають за рекурентною формулою:
Метод Ейлера відноситься до чисельних методів, які дають розв’язок у вигляді таблиці наближених значень шуканої функції y (x). Вибираючи досить малий крок h, будується система рівновіддалених точок xk = x 0 + kh, k = 0, 1, 2, …. Методом Ейлера значення y (xk)» yk обчислюють наближено за формулою yk +1 = yk + hf (xk; yk).
За методом Рунге—Кута обчислення наближеного значення yk +1 у точці xk +1 = xk + h проводиться за формулами: yk +1 = yk + D yk; D y k = де
Термінологічний словник Абсолютна похибка D наближеного числа a — абсолютна величина різниці між відповідними точним та наближеним числами. Відносна похибка d наближеного числа a — відношення абсолютної похибки D цього числа до модуля відповідного точного числа A. Гранична абсолютна похибка D a наближеного числа — число, не менше від абсолютної похибки цього числа. Гранична відносна похибка d a наближеного числа — будь-яке число, не менше, ніж відносна похибка цього числа. Значуща цифра наближеного числа а — будь-яка цифра в десятковому вираженні числа, відмінна від нуля, та нуль, якщо він розташований між значущими цифрами або є представником збереженого десяткового розряду. Решта нулів, що входять у склад наближеного числа та служать тільки для позначення його десяткових розрядів, не зараховуються до значущих цифр. Наближене число — число, яке незначно відрізняється від точного та замінює його в обчисленнях. Похибка (помилка) наближеного числа — різниця між відповідними точним та наближеним числами. Практичне заняття На практичному занятті проводиться оцінювання знань шляхом усного опитування та розв’язування практичних завдань. На усне опитування виносяться теми: — основні поняття, пов’язані з похибками обчислень; — поняття про наближення функції; — використання рядів; — інтерполяція; — чисельне диференціювання; — чисельне інтегрування; — прямі методи розв’язання систем лінійних рівнянь; — ітераційні методи розв’язання систем лінійних рівнянь; — нелінійні рівняння; — чисельне розв’язання диференційних рівнянь. Практичні завдання 1. Визначте, яка рівність точніша: 2. Обчисліть та визначте похибки результату: 3. Знайдіть наближено суму ряду 4. Обчисліть з точністю до 0,001 значення таких функцій:
5. Відділіть корені аналітично та уточніть один із них методом половинного ділення з точністю до 0,01: 3 x 4 + 4 x 3 – 12 x 2 – 5 = 0. 6. Відділіть корені графічно та уточніть один із них методом хорд з точністю до 0,01: x – sin x = 0,25. 7. Відділіть корені графічно та уточніть один із них методом дотичних з точністю до 0,001: tg(0,55 x + 0,1) = x 2. 8. Відділіть корені аналітично та уточніть один з них методом ітерацій з точністю до 0,001: x 3 + 2 x 2 + 2 = 0. 9. Використовуючи схему Гаусса, розв’яжіть систему рівнянь з точністю до 0,0001:
10. Методом ітерацій розв’яжіть СЛАР з точністю до 0,001:
11. Методом Зейделя розв’яжіть з точністю до 0,001 СЛАР, зведіть її до вигляду, зручного для ітерацій
12. Знайдіть наближене значення функції при даному значенні аргументу за допомогою інтерполяційного полінома Лагранжа:
13. Використовуючи першу чи другу інтерполяційну формулу Ньютона, обчисліть значення функції при даних значеннях аргументу.
14. За допомогою інтерполяційної формули Ньютона знайдіть значення першої та другої похідних при даних значеннях аргументу для функції, заданої у вигляді таблиці:
15. Обчисліть інтеграл 16. Обчисліть інтеграл 17. Обчисліть визначений інтеграл 18. За допомогою рядів обчисліть інтеграл 19. Використовуючи метод Ейлера, складіть таблицю наближених значень розв’язку диференційного рівняння y ¢ = x 2 + y 2, що задовольняє початкову умову y (0) = 0 на відрізку [0; 1], h = 0,1. Усі обчислення поведіть з точністю до чотирьох десяткових знаків. 20. Використовуючи метод Рунге—Кута, складіть табли- Завдання для перевірки знань 1. Як пов’язані між собою абсолютна та відносна похибки? 2. Наведіть відомі вам формули для розрахунку похибок. 3. Як можна використовувати ряди для наближеного обчислення функцій? 4. Назвіть відомі вам методи розв’язання алгебраїчних та трансцендентних рівнянь. 5. Чим відрізняються прості методи розв’язання СЛАР від ітераційних? Перерахуйте ці методи. 6. У чому полягає завдання інтерполяції? 7. Дайте геометричну інтерпретацію основним формулам чисельного інтегрування. 8. Сформулюйте задачу Коші та назвіть основні чисельні методи для її розв’язання.
Індивідуальна робота
Індивідуальна робота включає в себе самостійне опрацювання далі наведених питань. Форма контролю даної роботи — реферат, який необхідно здати на першому практичному занятті. Обсяг реферату має бути до двадцяти сторінок. Тема реферату: «Дискретний аналіз. Історичні аспекти розвитку». Зміст реферату: · Вступ. Складові дискретного аналізу та особливості їх об’єднання в рамках однієї дисципліни. · Історична обумовленість створення теорії множин. · Роль логічних та семантичних парадоксів у формуванні математичної логіки. · Теорія нечітких підмножин як перспективний розділ математики. · Зростання ролі інформаційних систем та технологій при розв’язанні соціально-економічних завдань. Місце чисельних методів у цьому процесі.
Поточний контроль засвоєння матеріалу з кожної теми здійснюється: · усним опитуванням, · виконанням практичних завдань, · письмовою роботою (тестом). У поточному контролі з кожної теми ставиться оцінка 0, 5 або 10. Оцінка «десять» ставиться тоді, якщо студент оволодів основним теоретичним матеріалом та продемонстрував практичні навички. Якщо студент уміє розв’язувати задачі, але не повністю володіє теоретичним матеріалом або добре засвоїв теоретичний матеріал, але не навчився розв’язувати практичні завдання, тоді він отримує п’ять балів. Якщо ж студент не знає теоретичного матеріалу та не вміє розв’язувати задачі, то він отримує за відповідну тему нуль балів. При підсумковому контролі враховується загальна кількість балів, отриманих студентом з кожної теми протягом семестру. Знання студентів оцінюються за п’ятибальною системою: · оцінку 5 отримують студенти, які набрали протягом курсу 55 або 60 балів; · оцінку 4 отримують студенти, які отримали протягом курсу 45 або 50 балів; · оцінку 3 отримують студенти, які одержали протягом курсу не менше 30-ти балів; · оцінку 2 отримують студенти, які не набрали протягом семестру 30-ти балів. Залік за результатами поточного семестру отримують студенти, які отримали оцінку 5, 4 або 3. Якщо з поважної причини студент не зміг отримати задовільну оцінку, то він складає залік, на який виносяться завдання з кожної теми, крім вступу (всього шість тем). Приклади завдань наведено в кінці кожної теми в розділі «Навчальні завдання».
1. Акимов О. Е. Дискретная математика. — Комсомольск-на-Амуре, 1996. — 117 с. 2. Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы: Уч. пособие. — М.: Наука, 1987. 3. Гладкий А. В. Математическая логика / Российский гос. гуманитарный ун-т. — М., 1998. — 497 с. 4. Горбатов В. А. Основы дискретной математики. — М.: Высшая школа, 1986. — 311 с. 5. Данилович В. П. Чисельні методи в задачах і вправах: Навч. посібник для студ. спец. «Прикладна математика» / ІСДО; Державний ун-т «Львівська політехніка». — К., 1995. — 248 с. 6. Донской В. И. Дискретная математика: Учеб. пособие. — Симферополь: СОНАТ, 2000. — 358 с. 7. Каханер Дэвид, Моулер Клив, Нэш Стивен. Численные методы и программное обеспечение. — М.: Мир, 1998. — 576 с. 8. Кобринский Н. Е., Майминас Е. З., Смирнов А. Д. Экономическая кибернетика. — М.: Экономика, 1982. 9. Коршунов Ю. М. Математические основы кибернетики. — М.: Энергия, 1972. 10. Кофман А. Введение в теорию нечетких множеств. — М.: Радио и связь, 1982. — 432 с. 11. Лиман Ф. М. Математична логіка і теорія алгоритмів: Навч. посібник для студ. фіз.-мат. спец. пед. вузів / Інститут змісту і методів навчання. — Суми: Слобожанщина, 1998. — 152 с. 12. Оленко А. Я., Ядренко М. Й. Дискретна математика: Навч.-метод. посібник / Національний ун-т «Києво-Могилянська академія». — К., 13. Столл Р. Множества, логика, аксиоматические теории. — М.: Просвещение, 1968. 14. Трохимчук Р. М. Теорія графів: Навч. посібник для студ. ф-ту кібернетики / Київський ун-т ім. Тараса Шевченка. — К.: РВЦ «Київський університет», 1998. — 57 с. 15. Турчак Л. И. Основы численных методов. — М.: Наука, 1986.
* На діаграмах істинні складні висловлення зображені у вигляді зафарбованих зон. [1] Надалі нечітку множину будемо позначати літерою, підкресленою пунктиром. Належність та неналежність будемо позначати, як і в теорії множин, Î та Ï. Нечітку належність, якщо в цьому виникне потреба, будемо позначати Î та Ï. означає, що х Î А, тобто «х є елементом А», означає, що х Ï А, тобто «х не належить А», означає, що х є елементом зі ступенем 0,8.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.119.241 (0.041 с.) |
 що збігається в інтервалі [– R; R ], який містить відрізок інтегрування [ a, b ].
що збігається в інтервалі [– R; R ], який містить відрізок інтегрування [ a, b ]. (24)
(24)
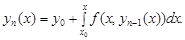


 чи
чи  .
. якщо a = 3,55 (±0,01); b = 2,0435 (±0,0004); c = 962,7 (±0,1).
якщо a = 3,55 (±0,01); b = 2,0435 (±0,0004); c = 962,7 (±0,1). з точністю до 0,001.
з точністю до 0,001.

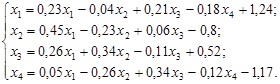

 за формулою трапецій з точністю до 0,001.
за формулою трапецій з точністю до 0,001. за формулою Сімпсона при n = 8 оцініть похибку результату.
за формулою Сімпсона при n = 8 оцініть похибку результату. розклавши підінтегральну функцію в ряд та взявши для обчислення три перші члени ряду. Оцініть похибку.
розклавши підінтегральну функцію в ряд та взявши для обчислення три перші члени ряду. Оцініть похибку. з точністю до 0,001.
з точністю до 0,001.

 5. Список літератури
5. Список літератури


