
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтерполяція та наближення функцій
Найпростіше завдання інтерполювання полягає в такому. На відрізку [ a, b ] задані n + 1 точки х 0, х 1,..., хn, які називаються вузлами інтерполяції, та значення деякої функції f (x) в цих точках y 0 = f (x 0), y 1 = f (x 1), …, yn = f (xn). Необхідно побудувати функцію F (x) (інтерполюючи функцію f (x)), що належить певному класу та набуває у вузлах інтерполяції тих самих значень, що й f (x). Геометрично це означає, що необхідно знайти криву y = F (x) певного типу, яка проходить через задану систему точок Mi (xi, yi), i = 1, 2, …, n. У такій постановці задача може мати нескінченну множину розв’язків або не мати їх зовсім. Для уникнення цієї проблеми найчастіше замість довільної функції F (x) шукають поліном Рn (x) степеня, не вищого від n, який задовольняє умови y 0 = Pn (x 0), Отриману інтерполяційну формулу, як правило, використовують для наближеного обчислення значень функції f (x) для значень аргументу x, які відрізняються від вузлів інтерполювання. Інтерполяційна формула Лагранжа. Нехай на відрізку [ a, b ] задано n + 1 різних значень аргументу: х 0, х 1,..., xn та відомі для функції y = f (x) відповідні значення y 0 = f (x 0), y 1 = f (x 1), …, yn = f (xn). Необхідно побудувати поліном Ln (x) степеня, не вищого від n, який має в заданих вузлах х 0, х 1,..., xn ті самі значення, що й функція f (x), тобто Ln (xi) = yi, i = 0, 1, …, n. Поліном
степеня n має таку властивість: Pk (xm) = 0, якщо k ¹ m та Pk (xk) = 1. Тому шуканий багаточлен має такий вигляд:
або
Формула (11) називається інтерполяційною формулою Лагранжа. Отриманий поліном Лагранжа єдиний. Формулу (11) можна виразити стисліше. Нехай w(х) = (х – х 0)(х – х 1)...(х – хn), тоді w¢(xk) = (xk – x 0)(xk – x 1)…(xk – xk –1)(xk – xk+ 1)…(xk – xn), отже,
Вузли інтерполяції називаються рівновіддаленими, якщо w(x) = hn +1 u (u – 1)(u – 2)…(u – n); w¢(xk) = (–1) n – k hnk!(n – k)!; x – xk = h (u – k). Підставляючи ці значення в формулу (12), отримаємо:
де W(u) = u (u – 1)(u – 2)…(u – n). Різниця Rn (x) = f (x) – Ln (x) називається залишковим членом інтерполяції. Якщо функція f (x) має на відрізку [ a, b ] всі похідні до (n + 1)-го порядку включно, то
де x залежить від х та лежить у середині відрізка [ a, b ]. Якщо
Скінченні різниці. Нехай функція y = f (x) задана табличними значеннями yk = f (xk) для системи рівновіддалених точок xk,
Перші скінченні різниці значень функції yk = f (xk) визначаються такими рівностями: D y 0 = y 1 – y 0; D y 1 = y 2 – y 1; …; D yn –1 = yn – yn –1. За першими різницями аналогічно обраховуємо значення різниць другого порядку: D2 y 0 = D(D y 0) = D y 1 – D y 0; D2 y 1 = D(D y 1) = D y 2 – D y 1; …; Різниці порядку m + 1 визначаються за різницями порядку m за допомогою рекурентної формули: D m +1 yk = D(D myk) = D myk +1 – D myk. Скінченні різниці кількох порядків зручно подавати у формі таблиць двох видів: горизонтальній або діагональній таблицях різниць.
Перша інтерполяційна формула Ньютона. Нехай задані рівновіддалені точки хk = x 0 + kh, а значення функції y = f (x) у цих точках: yk = f (xk), k = 0, 1,…, n. Введемо нову змінну u = (x – x 0)/ h або x = x + uh. Якщо u набуває значень 0, 1,..., n, то х набуває значень H (x 0 + uh) = a 0 + a 1 u + a 2 u (u – 1)(u – 2) +… Коефіцієнти а 0, а 1,..., аn знайдемо з умови H (x 0 + kh) = yk: y 0 = a 0; y 1 = a 0 + a 1; y 2 = a 0 + 2 a 1 + 2 a 2; …………………… yn = a 0 + na 1 + n (n – 1) a 2 + … + n! an. З цієї системи рівнянь послідовно знаходимо:
Підставивши знайдені коефіцієнти, отримаємо:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.159.150 (0.012 с.) |
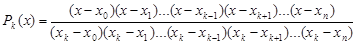 (10)
(10)
 (11)
(11) (12)
(12) (13)
(13) (14)
(14) то
то




