
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип гарантированного результатаСодержание книги Поиск на нашем сайте
Пусть имеется задача (9) для нее нет сначала выбирается ф-ция Ф( Ф( max Ф(
для нахождения в-та добавляем max, гарантируем себя от плохих вариантов.
Принцип парето. Построение множества оптимальных решений по парето (принцип - п.п.) при решени многокрит. задач мы пытаемся их свести к однокрит. т.к. для них существует хор. разработанные методы матем. програм-я. но к решению многокрит задач можно подойти и с др. позиций: попытаться сократить мн-во исходных в-тов исключения из неформального в-та, те решения, которые заведомо явл-ся плохими. пусть имеется задача многокрит оптимизации(6). здесь каждому значению
множество альтернатив эффективной (наилучшей) называется т. само множ-во всех эффектив. точек наз-ся областью решений оптимальныхпо парето (множество парето). оптимальность по парето означает что нельзя дальше улучшить значение одного из частных критериев, не ухудшая при этом значение хотя бы одного из остальных(достигли предельного состояния). в теории принятия решений сущ-ет термин п.п., закл. в том, что выбирать в качестве решения следует только тот вектор т.о. определение оптимального компромисс. решения позволяет разделить поиск нахождения решения задача многокритриальных оптимизации на 2 этапа: 1) построение множества множества парето, т.е. нехождение эф-х точек 2)выбор i-ого множества решения и точки наиболее предпочтительной точки с точки зр. ЛПР множество парето имеет весьма сложную природу. но его анализ дает дальнейш. информацию для ЛПР. т.е. эф-ых точек очень много надо выбрать одну. обычно выдвигаются разные предпочтения в завис. от своих интересов. н-р: в его распоряжении может оказаться некот. общий критерий: F(x) – пусть это суммар. сто-ть проекта, тогда max (min) F(x)но уже x где PGx(f1,f2,...fk) – это множество парето для ф-ции f(x) на множестве допустимых векторов Gx как построить множество парето? max Ф(x, λ) =
не всегда можно построить множество парето, можно только когда множество Gx – многогранник, а ф-ции fi есть лин. ф-ция. если множество парето явля. выпуклым, то увеличивая кол-во точек любой степенью точности можно построить многогранник, аппроксимирующий искомое множество парето.
|
||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.56.125 (0.005 с.) |

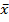 )
)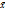 )= min
)= min  (11.1)
(11.1)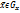
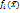 –множество критериев
–множество критериев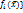
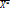 допустимого множества, в котором значение хотя бы одного критерия будет лучше по срав. со значением критериев
допустимого множества, в котором значение хотя бы одного критерия будет лучше по срав. со значением критериев 
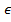 PGx(f1,f2,...fk)
PGx(f1,f2,...fk)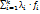 (x) → x* (13)
(x) → x* (13)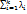 = 1,
= 1,  >0
>0 


