
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неопред. действия партнеров.Содержание книги Поиск на нашем сайте
Часто необходимо прин.решения,когда есть много субъектов и кажд. из них стремится достичь своей цели,имея для этого р-рсы. max
у кажд. i-го есть своя цель и ресурсы xi,часть Gi. н-р,имеются 2 субъекта: А: Б: когда f= -φ – антогонистич.ситуация, В этом случае выдвиг. гипотеза информир. субъектов: 1) в момент принятия решения А,известно действие субъекта Б. 2)наоборот 3)ни А,ни Б ничего не знают. 1.использ. принципа Парето для принятия компромисс. решения 2. принцип анализ ситуации равновесия. В данной ситуации берется седловая точка,к-я опред:
причем
т. Из всех min вариантов берем max-ый min-м.
Осн. подходы к решению задач многокритериальной оптимизации 1) априорные процедуры – сведение многокритериальных задач к однокритериальным с помощью копромисса и решающих правил. 2) построение множества по паретто альтернатив и выбор из этого множества альтернативы наиболее предпочтительной с т.зр. ЛПР 3) апостериорные процедуры (аксиоматический подход на базе теории полезностей для построения ф-ций предпочтения ЛПР) 4) адаптивный подход – человекомашинные процедуры для выявления предпочтения ЛПР одновременно с исследованием множества альтернатив в интерактивном режиме.
разбираем из них первые 2. Априорные процедуры пусть имеется задача(6). сведение многокр-ой задачи к однокр-ой –это наиболее употребительный способ преодоления неопределенности цели,т.е. решение задач многокритер. оптимизации. причем правило свертывания м.б. выработаны по-разному и неизвестно какое из них следует предпочесть. вибирая правила свертывания без достаточ. оснований (их протсо нет) вводят задачу принятия решений такой произвол., кот. обеспечивает всю дальнейшую работу. н-р: для примера (5) можно выбрать допустим f( f( и какой из них истинный - неизвестно. причем в каждом случае получится свое решение. было много критериев, остался один. куда делись остальные? или мы учитываем их в ограничениях или же они учитываются в обобщенном критерии. Линейная свертка для задачи (6) в этом случае вводится критерий:
max Ф(
получается ранжирование критериев и недостаток метода: если критерии имеют разный порядок, то обобщенный не будет их всех учитывать. Принцип справедливого компромисса критерий берется след. образом. имеет разный порядок
Выделение глав. критерия max
согласно дан. подходу выделяется один глав. критерий max
данная задача решается методом ЗЛП, если дан. задача разрешима, то ее решение принимается в качестве решения исход. задачи (9) или на основе анализа полученного решения устанавлив-ся новые контрольные показатели 2ой случай: задача (10) не имеет решения. в этом случае берем нов. контр. показатели:
приходится уступить и снова решаем.
|
||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.232 (0.005 с.) |

 (
( ) (4)
) (4)
 (5)
(5) (6)
(6) (7)
(7) (8)
(8) (9)
(9) - седловая точка
- седловая точка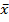 ) - F(
) - F(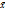 ) =
) = 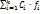 (
(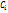 – положит. числа, причем
– положит. числа, причем  = 1
= 1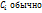 результат экспертизы. они отображают предпочтение исследователя, о содержании компромисса, кот. он принимает.
результат экспертизы. они отображают предпочтение исследователя, о содержании компромисса, кот. он принимает.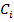 как будто явл. весовыми критериями.
как будто явл. весовыми критериями. ) =
) =  (8)
(8)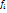 (
(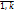 (9.1)
(9.1)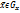
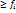 *, i=
*, i=  (
( (10.2)
(10.2)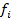 * (мы их усиливаем) и снова задачу решаем.
* (мы их усиливаем) и снова задачу решаем. * кот. меньше старых
* кот. меньше старых


