
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Градиентные методы. Метод наискорейшего спускаСодержание книги Поиск на нашем сайте
Градиентные методы. Метод наискорейшего спуска Применение класс. методов Мат. анализа для нахождения экстремума целев. ф-ции сопряжено большими трудностями.1) только необходимо условие экстремума: 2) приходиться решать систему нелинейных уравнений 3) экстремум может нах-ся на границе области. Эффективным м-дом решения ЗНП яв-ся градиентный метод. Градиент – вектор направленное по нормали к поверхности постоянного уровня, где выполняется условие. f( grad f( Градиент по направлению совпадает с направлением наискорейшего возрастания целевой функции f( Благодаря этому способу градиент примен-ся для решения ЗНЛП. Алгоритм град м-да может быть записан след. обр.Градиент- обычно для решения безусловных задач оптимизации.Рабочая формула имеет вид:
Есть простая формула: где Условия окончания когда выполняется условие
Метод наискорейшего спуска Это тоже град метод.Выбирается начальная точка, в кот вычисляется град и по данному направлению совершается движение (шаг), т.е. спуск или подъем.Если есть улучшение, то продолжаем движение в том же направлении.Т.о. нашли след точку, в кот вычисляется град-т и продолж-ся аналогичное движение пока не найдем оптимум.Данный метод быстрее приводит к оптимуму.
Безградиентные методы существует гр. безградентных методов, которые в процессе нахождения экстремума использует и информацию, получаемые от сравнительного анализа значений целевой функции в различных точках (в результате очередного шага). безград. методы исп-ют производ. методы: Метод сканирования. Суть: последний просмотр значений целевой функции в ряде точек, принадлежащих допустимой области и нахождение среди них точек, в которых достигается экстремум целевой функции.
0сн. достоинство метода: при достаточно «густом» расположении удается найти глобальный экстремум. недостаток: много точек - много вычислений. Модифицированный метод. сканирования. применяется чаще на практике. р-н разбивается на мелкие шаги.
Симплекс-метод (Кельдера-Нида). осн. идея закл. в след.: по известным значениям целевой функции в вершинах выпуклого многогранника, называемого симплексом, определяется направление, в котором требуется сделать очередной шаг, чтобы получить наиб. уменьшение (увеличение) ц.ф. схема поиска при этом основана на слежении за изменением значений значений ц.ф. в вершинах симплекса (тетраэдр – 3хмерн). главный здесь является отражение – процесс нахождения вершины нового симплекса, расположенного симметрично относительно плоскости, проходящей через одну из сторон исходного симплекса. выбор направления поиска вершины нового симплекса определяется положением той вершины исходного симплекса, в котором ц.ф. имеет наихудшее значение (если min, то большое значение). новая точка называется дополнением наихудшей точки если есть улучшение значения нового точки для нового симплекса. если нет улучшения, возвращается в исходный симплекс и находим следующую по значению наилучшую точку. все сводится к нахождению координат нов. точки. решается задача безусловной оптимизации. есть модифицированный симплекс-метод, в котором процесс нахождения нов. величины в сторону симплекса или сжимается или растягивается. это есть метод нельдера-нида. Метод случайного поиска согласно этому методу: перебор случ. значений независим. переменных найти оптимум и ц.ф. или направление к нему. а) «слепой поиск»: из допустимой области берется случ. точка Ха, вычисляется в ней значение функции, далее берем след. случ. точку. значения в двух точках сравниваем и записываем где лучше. далее очередную точку до тех пор, пока не найдем оптимум. б) метод случ. направлений
к=0,1,2,3...
h – const (парметр) ЗНП и методы его решения имеется з-ча max(min) { если хотя бы одна из ф-ий яв-ся нелин, то з-ча наз-ся ЗНП. Для решения з-чи НП не сущ-ет станд. методов реш-ия. Выбор метода решения зависит от содержания з-чи и опыта исследователя.М-д ЗНП может быть охарактеризована как многошаговые или как методы послед-го улучшения исходного решения.
Начальное значение
При решение задачи возникает 2 трудности: 1) выбор подходящих начальных значений 2) глобальный экстремум Эффективность методов ЗНП опред-ся след св-ми: - точность в поисках -надежность метода - скорость сходимости (к) Условные и безусловные ЗНП Если в системе или в уравнении отсутствует ограничения, то задача наз-ся з-чей безусловной оптимизации. Безусловная задача решается легче,чем условная з-ча, поэтому наряду с прямым методом решения услов задач часто применяется метод преобразования условных задач в бузуслов оптимизации, путем введения штрафных ф-ций. метод является одним из эффективных методов, позволяющих решать много задач оптимизации (найти глобальный экстремум). сущность метода: объект исследования и анализа не сама ц.ф., а некоторая другая функция Ψ(L), образуемая в результате преображения ф. f( если ц.ф.. f(
Метод штрафных функций
В кач-ве штраф. ф-ии можно взять функцию
Алгоритм решения задачи min f 1) выбир нач точку 2) при k=1,2,3,..., начиная с точки
Если на каждом шаге алгоритма удается найти глобальн min ф-цию Обычно
примечание. Если решается max(min) {
Алгоритм гомори 3.1 Постановка полностью целочисленной задачи линейного программирования Минимизировать ф-ю 3.2 Краткое описание алгоритма Гомори Сначала находим оптимальное решение непрерывной задачи (применяется прямой или двойственный симплекс-метод). Пусть бащисные переменные выражены через свободные след. образом: Это может быть записано как Тогда, если предположить, что l -ая переменная оптимального решения приняла др. значение, то введем новое ограничение Это будет дополнительная строка в симплекс-таблице. Далее решаем задачу двойственным симплекс-методом (при выборе отрицательного элемента в столбце свободных членов это будет
М-д случайного поиска. Согласно этому методу перебор случайных значений независ. переменных найти оптимум ц. ф. или направление к нему. - слепрой поиск: из допустимой области берется случайная точка - метод случайных направлений.
Априорные процедуры пусть имеется задача(6). сведение многокр-ой задачи к однокр-ой –это наиболее употребительный способ преодоления неопределенности цели,т.е. решение задач многокритер. оптимизации. причем правило свертывания м.б. выработаны по-разному и неизвестно какое из них следует предпочесть. вибирая правила свертывания без достаточ. оснований (их протсо нет) вводят задачу принятия решений такой произвол., кот. обеспечивает всю дальнейшую работу. н-р: для примера (5) можно выбрать допустим f( f( и какой из них истинный - неизвестно. причем в каждом случае получится свое решение. было много критериев, остался один. куда делись остальные? или мы учитываем их в ограничениях или же они учитываются в обобщенном критерии. Линейная свертка для задачи (6) в этом случае вводится критерий:
max Ф(
получается ранжирование критериев и недостаток метода: если критерии имеют разный порядок, то обобщенный не будет их всех учитывать. Выделение глав. критерия max
согласно дан. подходу выделяется один глав. критерий max
данная задача решается методом ЗЛП, если дан. задача разрешима, то ее решение принимается в качестве решения исход. задачи (9) или на основе анализа полученного решения устанавлив-ся новые контрольные показатели 2ой случай: задача (10) не имеет решения. в этом случае берем нов. контр. показатели:
приходится уступить и снова решаем. Принцип парето. Построение множества оптимальных решений по парето (принцип - п.п.) при решени многокрит. задач мы пытаемся их свести к однокрит. т.к. для них существует хор. разработанные методы матем. програм-я. но к решению многокрит задач можно подойти и с др. позиций: попытаться сократить мн-во исходных в-тов исключения из неформального в-та, те решения, которые заведомо явл-ся плохими. пусть имеется задача многокрит оптимизации(6). здесь каждому значению
множество альтернатив эффективной (наилучшей) называется т. само множ-во всех эффектив. точек наз-ся областью решений оптимальныхпо парето (множество парето). оптимальность по парето означает что нельзя дальше улучшить значение одного из частных критериев, не ухудшая при этом значение хотя бы одного из остальных(достигли предельного состояния). в теории принятия решений сущ-ет термин п.п., закл. в том, что выбирать в качестве решения следует только тот вектор т.о. определение оптимального компромисс. решения позволяет разделить поиск нахождения решения задача многокритриальных оптимизации на 2 этапа: 1) построение множества множества парето, т.е. нехождение эф-х точек 2)выбор i-ого множества решения и точки наиболее предпочтительной точки с точки зр. ЛПР множество парето имеет весьма сложную природу. но его анализ дает дальнейш. информацию для ЛПР. т.е. эф-ых точек очень много надо выбрать одну. обычно выдвигаются разные предпочтения в завис. от своих интересов. н-р: в его распоряжении может оказаться некот. общий критерий: F(x) – пусть это суммар. сто-ть проекта, тогда max (min) F(x)но уже x где PGx(f1,f2,...fk) – это множество парето для ф-ции f(x) на множестве допустимых векторов Gx как построить множество парето? max Ф(x, λ) =
не всегда можно построить множество парето, можно только когда множество Gx – многогранник, а ф-ции fi есть лин. ф-ция. если множество парето явля. выпуклым, то увеличивая кол-во точек любой степенью точности можно построить многогранник, аппроксимирующий искомое множество парето.
Симплек метод реш ЗЛП Универсальным методом реш ЗЛП явл=ся симплекс метод, кот непосредственно примен-ся. Баз решение опред. координаты вершин многогранника реш=ий и из них необход найти ту вершину, кот доставляет min целев ф-ии f(x). При больших числах ограничения n и числа неизвестных m найти оптимальное решение трудно. Max яисло переборов будет 2 этапа: 1. нахождение первоначальн баз реш 2. отправляясь от исход баз решения при помощи симплек метода нахожд-ие оптим реш-ия. Это достигается путем перемены местами одной из базисн переменных некот небазисн переменной, при этом значение баз. перем-ой увеличиваем до некот. значения, кот опред-ся ограничениями задачи. Переменные: -базисные r - небазисные, применяются равными 0. Каждый шаг приближает к min
Обычно ЗЛП решается в ручную с помощью симплекс таб. Иногда вместо исходной ЗЛП выгоднее решать другую задачу, называемую двойственной, когда число ограничений гораздо больше число значений.
Неопределенность цели. стремление получить max доход при минимальных затратах. говорит о наличии по крайней мере 2 критериев оптимизации. max f(
min F(
тем не менее мы будем предполагать, что задача выбора ед. альтернативы имеет решение. наличие ед. алтернативы (решения) говорит от том, что найденная альтернатива лучше в некотором смысле тех альтернатив, кот. не выбираются. реальное решение(альтернатива) всегда будет каким-то компромиссом, каким-то соченанием требуемых качеств(альтернатив, критериев), но каких исследователю заранее неизвестно. т.о. осн. проблема состоит не в том, что есть операции одноцелевого и многоцелевого хар-ра, а в том, что есть операции, цель которых извества исследователю. и которых не известна. такая ситуация вычислительных операция наз-ся неопределенностью выбора цели. всё это есть проблема многокритериальности (неопределенности цели) неопределенность цели требует привлечения доп. гипотез, если мы хотим однозначно сформулировать цель операции возникает проблема: критериев много(к штук), а цель одна.
max
если критериев от 2 и более, то это многокритериальная задача. (6) – матем. постановка задачи многокритериальной оптимизации возникновение нескольких критериев или векторного критерия 1. состоит в построении процедур, выявления предпочтений лица, принимающего решение(ЛПР) на языке векторных оценок алтернатив – это задача многокритериальн. оптимизации 2. связана с построением процедур отсеивания плохих альтернатив. отсеивание плохих альтернатив – выделение альтернатив, max – ных по данной системе критериев. неопределенность цели носит неустранимый характер, т.е. не может быть достаточно обоснованных исключена из рассмотрения до решения.
Градиентные методы. Метод наискорейшего спуска Применение класс. методов Мат. анализа для нахождения экстремума целев. ф-ции сопряжено большими трудностями.1) только необходимо условие экстремума: 2) приходиться решать систему нелинейных уравнений 3) экстремум может нах-ся на границе области. Эффективным м-дом решения ЗНП яв-ся градиентный метод. Градиент – вектор направленное по нормали к поверхности постоянного уровня, где выполняется условие. f( grad f( Градиент по направлению совпадает с направлением наискорейшего возрастания целевой функции f( Благодаря этому способу градиент примен-ся для решения ЗНЛП. Алгоритм град м-да может быть записан след. обр.Градиент- обычно для решения безусловных задач оптимизации.Рабочая формула имеет вид:
Есть простая формула: где Условия окончания когда выполняется условие
Метод наискорейшего спуска Это тоже град метод.Выбирается начальная точка, в кот вычисляется град и по данному направлению совершается движение (шаг), т.е. спуск или подъем.Если есть улучшение, то продолжаем движение в том же направлении.Т.о. нашли след точку, в кот вычисляется град-т и продолж-ся аналогичное движение пока не найдем оптимум.Данный метод быстрее приводит к оптимуму.
Безградиентные методы существует гр. безградентных методов, которые в процессе нахождения экстремума использует и информацию, получаемые от сравнительного анализа значений целевой функции в различных точках (в результате очередного шага). безград. методы исп-ют производ. методы: Метод сканирования. Суть: последний просмотр значений целевой функции в ряде точек, принадлежащих допустимой области и нахождение среди них точек, в которых достигается экстремум целевой функции.
0сн. достоинство метода: при достаточно «густом» расположении удается найти глобальный экстремум. недостаток: много точек - много вычислений. Модифицированный метод. сканирования. применяется чаще на практике. р-н разбивается на мелкие шаги.
Симплекс-метод (Кельдера-Нида). осн. идея закл. в след.: по известным значениям целевой функции в вершинах выпуклого многогранника, называемого симплексом, определяется направление, в котором требуется сделать очередной шаг, чтобы получить наиб. уменьшение (увеличение) ц.ф. схема поиска при этом основана на слежении за изменением значений значений ц.ф. в вершинах симплекса (тетраэдр – 3хмерн). главный здесь является отражение – процесс нахождения вершины нового симплекса, расположенного симметрично относительно плоскости, проходящей через одну из сторон исходного симплекса. выбор направления поиска вершины нового симплекса определяется положением той вершины исходного симплекса, в котором ц.ф. имеет наихудшее значение (если min, то большое значение). новая точка называется дополнением наихудшей точки если есть улучшение значения нового точки для нового симплекса. если нет улучшения, возвращается в исходный симплекс и находим следующую по значению наилучшую точку. все сводится к нахождению координат нов. точки. решается задача безусловной оптимизации. есть модифицированный симплекс-метод, в котором процесс нахождения нов. величины в сторону симплекса или сжимается или растягивается. это есть метод нельдера-нида. Метод случайного поиска согласно этому методу: перебор случ. значений независим. переменных найти оптимум и ц.ф. или направление к нему. а) «слепой поиск»: из допустимой области берется случ. точка Ха, вычисляется в ней значение функции, далее берем след. случ. точку. значения в двух точках сравниваем и записываем где лучше. далее очередную точку до тех пор, пока не найдем оптимум. б) метод случ. направлений
к=0,1,2,3...
h – const (парметр)
|
||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.49 (0.019 с.) |

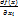 =0
=0 = const с алгебраической величиной, равной
= const с алгебраической величиной, равной  , где n- нормаль к поверхности пост. уровня.
, где n- нормаль к поверхности пост. уровня.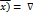 f(
f( ,
, 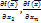 )
) , т.е. это кратчайший путь к max f(
, т.е. это кратчайший путь к max f(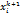 =
= 
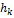 - шаг спуска(параметр)
- шаг спуска(параметр) =
=  *
*  ,
,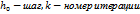
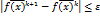

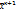 =
= 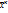 + h
+ h 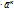
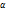 - случ. вектор
- случ. вектор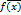

 =
=  , где к- номер шага итерации,
, где к- номер шага итерации,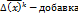 ,это шаг. к=0,1,2,3,4
,это шаг. к=0,1,2,3,4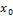 задается или выбирается. все сводится к нахождению
задается или выбирается. все сводится к нахождению 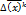 . Условие остановки
. Условие остановки 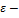 задан. точность решения задачи.
задан. точность решения задачи.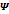 – преобразования
– преобразования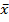 )
) является монотонно убывающей и ноль этой функции соотвествует значению max ц.ф. f(
является монотонно убывающей и ноль этой функции соотвествует значению max ц.ф. f(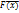 =f
=f 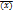 +
+ 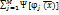 - безусловная задача оптимизации
- безусловная задача оптимизации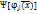 -штрафная ф-ия, путем добавления к целев. ф-ии одной или нескольких функций, учитывающие ограничения. Все условия учитываются в штраф. ф-иях.
-штрафная ф-ия, путем добавления к целев. ф-ии одной или нескольких функций, учитывающие ограничения. Все условия учитываются в штраф. ф-иях.
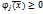 ,
, 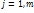 и
и 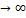 если это условие не выполняется.Поэтому если все условия выполняются, то min совпадает, а если не вып-ся, то добав шт ф-ций.
если это условие не выполняется.Поэтому если все условия выполняются, то min совпадает, а если не вып-ся, то добав шт ф-ций. ,
, 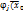 )>0,
)>0, 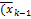 ) решается задача безусловной оптимизации, в результате определяется очередная точка
) решается задача безусловной оптимизации, в результате определяется очередная точка  )
)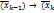 ) и т. д. процесс повторяется.
) и т. д. процесс повторяется.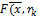 ) по x, то последовательность
) по x, то последовательность 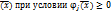 при
при 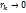
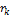 выбирают:
выбирают: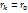 /
/ 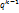 причем q>1- const,
причем q>1- const, 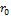 =[50;100]
=[50;100]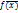
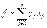 при ограничениях
при ограничениях  , где
, где 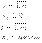
 , где
, где 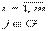 G – множество индексов свободных переменных в оптимальном решении непрерывной задачи.
G – множество индексов свободных переменных в оптимальном решении непрерывной задачи. , где [ x ] – целая часть х, а х0 – дробная.
, где [ x ] – целая часть х, а х0 – дробная.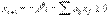 , где
, где 
 )
) выполняется в ней значение ф-ии, далее берем след случ. точку, значение в двух точках сравниваем и запоминаем где лучик, далее очередную точку.До тех пор не найдем оптимум.
выполняется в ней значение ф-ии, далее берем след случ. точку, значение в двух точках сравниваем и запоминаем где лучик, далее очередную точку.До тех пор не найдем оптимум.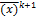 =
= 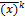 +h*
+h* 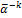 , k- 0,1,2,3....,
, k- 0,1,2,3...., 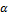 - случ. вектор.
- случ. вектор.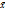 ) =
) = 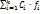 (
(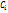 – положит. числа, причем
– положит. числа, причем  = 1
= 1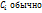 результат экспертизы. они отображают предпочтение исследователя, о содержании компромисса, кот. он принимает.
результат экспертизы. они отображают предпочтение исследователя, о содержании компромисса, кот. он принимает.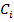 как будто явл. весовыми критериями.
как будто явл. весовыми критериями.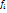 (
(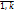 (9.1)
(9.1)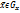
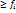 *, i=
*, i=  (
( (10.2)
(10.2)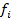 * (мы их усиливаем) и снова задачу решаем.
* (мы их усиливаем) и снова задачу решаем. * кот. меньше старых
* кот. меньше старых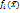 –множество критериев
–множество критериев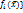
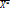 допустимого множества, в котором значение хотя бы одного критерия будет лучше по срав. со значением критериев
допустимого множества, в котором значение хотя бы одного критерия будет лучше по срав. со значением критериев 
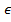 PGx(f1,f2,...fk)
PGx(f1,f2,...fk)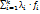 (x) → x* (13)
(x) → x* (13)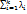 = 1,
= 1,  >0
>0  , поэтому необходимо иметь схему, позволяющую исходя из известного баз реш-я найти оптимальное решение. Такой схемой яв-ся симплек метод.
, поэтому необходимо иметь схему, позволяющую исходя из известного баз реш-я найти оптимальное решение. Такой схемой яв-ся симплек метод.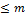
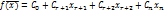

 (
(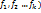 оценки качества альтернатив порождает 2 осн. задачи:
оценки качества альтернатив порождает 2 осн. задачи:


