
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Багатопроменева інтерференція
де a = 2p - Nd, а з прямокутного трикутника ОFB бічна сторона
Приймаючи, що
одержимо величину результуючої амплітуди А у вигляді
або інтенсивність
де І1 ~ A12 ¾ інтенсивність окремої хвилі. Головні максимуми інтерференції спостерігаються в тих точках, де кути d = 0 або вони кратні 2p. Для цих випадків вектори амплітуд лежать на одній прямій і модуль їх суми буде максимальний. Таким чином умова максимуму має вигляд d = ± 2np, (3) де n = 0,1,2,3,.... ¾ порядок максимумів. Амплітуда та інтенсивність коливань у головних максимумах дорівнюють А = NA1, I = N2I1. (4) Інтерференційні мінімуми (А = 0) спостерігаються в точках де d = ±2рp/N, (5)
b). Якщо число інтерференційних хвиль необмежено збільшувати, а їх амплітуди А1 та зсуви фази зменшувати так, щоб величини N×A1 та N×d залишались обмеженими й рівними А0 та Dj, відповідно, то векторна діаграма прийме вигляд, показаний на Мал.147. Послідовність векторів
або
При
Інтерферометр Майкельсона
Інтерферометр Майкельсона, принципова схема якого показана на Мал.149, використовується для точних вимірювань показника заломлення світла газів та їх залежності від температури, тиску й вологості. Світло від джерела S падає під кутом Різниця оптичного ходу
Голографія У 1948 році Д.Габор запропонував голографічний метод одержання зображень предметів. Голографія є метод одержання просторових зображень (голограми) предметів шляхом фотографічного запису результатів інтерференції двох когерентних лазерних пучків світла. Для одержання голограми лазерне випромінювання поділяють на два пучки 1 ¾ опорний і 2 ¾ сигнальний (предметний), що розсіюється об'ємною поверхнею деякого предмета (див.Мал.150). Після зведення пучка 1 і розсіяного пучка 2' на фотопластинці, остання зафіксує просторову картину їх інтерференції. Після проявлення фотопластинки одержимо голограму ¾ узор із малих областей різного роду почорніння фотоемульсії, який не має ніякої схожості з предметом. Голограма фіксує амплітудні й фазові співвідношення у розсіяному від предмета світлі, які визначаються взаємним просторовим розташуванням частин предмета.
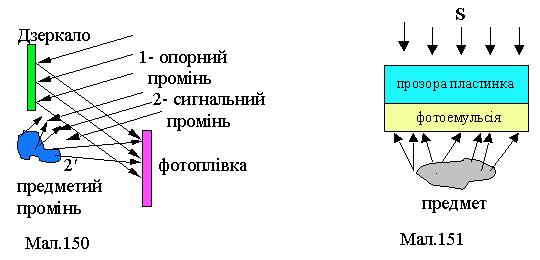
Відтворення зображення предмета з голограми відбувається шляхом освітлення її таким же опорним пучком світла, як і при записі голограми. Якщо товщина фотоплівки мала, то голограму називають двовимірною і зображення предмета можна спостерігати не тільки при освітленні опорним лазерним пучком, а й світлом, наприклад, ртутної лампи. Однак освітлення голограми опорним світлом дає повне і якісне зображення предмета. При утворенні голограми на фотопластинці (див.Мал.151), усі її ділянки освітлюються розсіяним випромінюванням від усіх частин предмета, а тому кожна частинка голограми містить усю інформацію про предмет і усі разом вони дають чітке зображення предмета. Чим менша частинка голограми використовується ти менш чітким буде образ предмета. При відтворенні образу предмета він створюється як відбитим так і випромінюванням, що пройшло голограму. Відбита хвиля створює уявне зображення, а та, що пройшла створює дійсне зображення.
Використання як опорного та сигнального лазерного випромінювання трьох основних кольорів (червоний, зелений, синій) дає змогу одержати кольорову об'ємну голограму у прозорій фотоплівці товщиною ~ 15¾20 мкм. Випромінювання від лазерів S проходить через пластинку й фотоплівку, розсіюється предметом і повертається у шар фотоемульсії, де інтерферує з падаючим випромінюванням. Відновлення кольорового зображення можливе у звичайному білому світлі. У 1962 році Ю.М.Денисюк вперше одержав об'ємну голограму у товстій фотоемульсійній плівці. Такі голограми подібні до просторових дифракційних решіток. Відтворення зображень предметів з таких голограм можливо у білому світлі. Голографія відкриває широкі перспективи у створенні великих систем пам'яті обчислювальних машин, систем інформаційного пошуку, систем розпізнавання образів і, нарешті, у створенні систем стереоскопічного кольорового кіно та телебачення.
Дифракція
Явище відхилення світла від прямолінійного розповсюдження в середовищі з різко вираженими оптичними неоднорідностями називається дифракцією. До згаданих явищ відносять огинання світлом макроперешкод, проходження через отвори та інше. В результаті в геометричній тіні спостерігаються освітлені та затемнені області. Розрізнюють дифракцію сферичних хвиль – дифракція Френеля та дифракцію плоских хвиль – дифракція Фраунгофера.
Принцип Гюйгенса-Френеля
Положення хвильового фронту у будь-який момент часу можна визначити за принципом Гюйгенса. Згідно цього принципу усі точки хвильової поверхні є уявними (фіктивними) вторинними точковими джерелами когерентних коливань. Ці джерела випромінюють сферичні хвилі від генеруючого джерела, а у напрямі до нього вони взаємно компенсуються. Для знаходження положення хвильового фронту в наступний момент часу потрібно побудувати огинаючу поверхню хвильових сферичних поверхонь указаних точкових джерел.
Розрахунок інтенсивності випромінювання у деякій точці М простору, у тому числі і тоді коли ця точка знаходиться у області геометричної тіні проводиться за принципом Френеляу такий спосіб. а) Джерело коливань S0 замінюється еквівалентною йому системою уявних вторинних джерел ¾ малих ділянок dS будь - якої замкненої допоміжної хвильової поверхні S, яка охоплює джерело S0 і не охоплює точку М, що знаходиться на відстані r від dS; б) амплітуда dЕ коливань, що збуджуються в точці М вторинним джерелом задається виразом
де
де інтегрування проводиться по усій допоміжній хвильовій поверхні.
Зони Френеля
Для спрощення розрахунку амплітуди коливань
де
Для не дуже великих і, приймаючи, що l<<L, із попереднього рівняння можна одержати
Площа поверхні і - ої зони Френеля дорівнює різниці площ поверхонь сусідніх сферичних сегментів
і не залежить від номера зони, тобто є сталою величиною. Тому можна покласти, що
і величину результуючої амплітуди коливань у точці М можна представити так
Згідно з попереднім виразом, доданки у дужках дадуть 0 і остаточно отримаємо
Розрахуємо кількість зон, яку потрібно приймати до уваги при розрахунку результуючої амплітуди. Відстань найвіддаленішої N-ої зони Френеля до точки М дорівнює довжині дотичної, проведеної з М до кола, тому
і при
|
|||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.190.167 (0.022 с.) |
 a). Інтерференція N когерентних хвиль із послідовним зсувом фаз на величину d і рівними за величиною амплітудами (нехай амплітуда є А1) може бути розрахована графічно на фазовій площині, де коливання представляються амплітудними векторами із певними початковими фазами. Їх сума
a). Інтерференція N когерентних хвиль із послідовним зсувом фаз на величину d і рівними за величиною амплітудами (нехай амплітуда є А1) може бути розрахована графічно на фазовій площині, де коливання представляються амплітудними векторами із певними початковими фазами. Їх сума 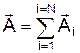 визначається за правилом багатокутника, який утворюється розміщенням початку послідуючого вектора у вершині попереднього. Результуюча амплітуда А є вектор, проведений із початку першого вектора у кінець останнього (див.Мал.145). Вектори А і, як показано на малюнку, є частиною правильного багатокутника (число його сторін дорівнює
визначається за правилом багатокутника, який утворюється розміщенням початку послідуючого вектора у вершині попереднього. Результуюча амплітуда А є вектор, проведений із початку першого вектора у кінець останнього (див.Мал.145). Вектори А і, як показано на малюнку, є частиною правильного багатокутника (число його сторін дорівнює  ). З малюнка видно, що
). З малюнка видно, що ,
, .
. ,
,
 (1)
(1) , (2)
, (2)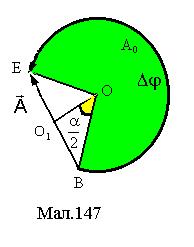 число р приймає будь-які цілі значення, крім тих, які кратні N. Між парою сусідніх мінімумів знаходиться головний або побічний максимум. При великому числі інтерферуючих хвиль інтенсивність побічного максимуму мізерно мала порівняно з інтенсивністю головного максимуму. На Мал.146 представлено графік інтенсивності інтерференції двох та трьох хвиль у залежності від
число р приймає будь-які цілі значення, крім тих, які кратні N. Між парою сусідніх мінімумів знаходиться головний або побічний максимум. При великому числі інтерферуючих хвиль інтенсивність побічного максимуму мізерно мала порівняно з інтенсивністю головного максимуму. На Мал.146 представлено графік інтенсивності інтерференції двох та трьох хвиль у залежності від  .
. перетвориться в дугу кола А0, а її кутова величина стане рівною Dj. Радіус кола
перетвориться в дугу кола А0, а її кутова величина стане рівною Dj. Радіус кола 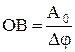 . Амплітуда результуючого коливання
. Амплітуда результуючого коливання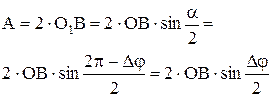 ,
, . (6)
. (6) Умови мінімумів інтерференції можна задати рівнянням
Умови мінімумів інтерференції можна задати рівнянням (m = 1,2,3,...). (7)
(m = 1,2,3,...). (7) , А = А0 ¾ центральний максимум. На Мал.148 представлена залежність відносної величини інтенсивності інтерференції від зсуву фази
, А = А0 ¾ центральний максимум. На Мал.148 представлена залежність відносної величини інтенсивності інтерференції від зсуву фази  . З точки зору величини результуючої інтенсивності актуальним є розгляд випадків коли
. З точки зору величини результуючої інтенсивності актуальним є розгляд випадків коли  на плоскопаралельну скляну пластинку
на плоскопаралельну скляну пластинку 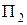 , задня стінка якої посріблена. Частина світла від неї відбивається (промінь 1) до дзеркала
, задня стінка якої посріблена. Частина світла від неї відбивається (промінь 1) до дзеркала  . Далі промінь 1 відбивається від
. Далі промінь 1 відбивається від  і далі до дзеркала
і далі до дзеркала  . Цей промінь відбивається від
. Цей промінь відбивається від  , двічі проходячи через неї. Від посріблення пластинки
, двічі проходячи через неї. Від посріблення пластинки  ,
, де
де  ¾ відстані від точки О до дзеркал
¾ відстані від точки О до дзеркал  ¾ показник заломлення повітря. Якщо
¾ показник заломлення повітря. Якщо  , то спостерігається максимум інтерференції. Переміщення одного із дзеркал на відстань
, то спостерігається максимум інтерференції. Переміщення одного із дзеркал на відстань  призводить до появи мінімуму. Таким чином по зміні інтерференційної картиниможна оцінити малі переміщення одного із дзеркал. Якщо замість пластин використовувати кювети ¾ порожнинні скляні ємності за формою паралелепіпеда, заповнені повітрям або іншим газом чи рідиною, то можна вимірювати їх показники заломлення у залежності, наприклад, від температури, від тиску та інше. Зміна показника заломлення світла розраховується за зміною інтерференційної картини. Похибки вимірювання показника заломлення світла за допомогою інтерферометра Майкельсона становить
призводить до появи мінімуму. Таким чином по зміні інтерференційної картиниможна оцінити малі переміщення одного із дзеркал. Якщо замість пластин використовувати кювети ¾ порожнинні скляні ємності за формою паралелепіпеда, заповнені повітрям або іншим газом чи рідиною, то можна вимірювати їх показники заломлення у залежності, наприклад, від температури, від тиску та інше. Зміна показника заломлення світла розраховується за зміною інтерференційної картини. Похибки вимірювання показника заломлення світла за допомогою інтерферометра Майкельсона становить  .
.
 , (1)
, (1) ¾ амплітуда коливань джерела
¾ амплітуда коливань джерела  , функція
, функція  визначає залежність вторинного випромінювання від кута a між зовнішньою нормаллю до хвильової поверхні й напрямком від dS до М, яка монотонно зменшується від 1 при a = 0 до 0 при
визначає залежність вторинного випромінювання від кута a між зовнішньою нормаллю до хвильової поверхні й напрямком від dS до М, яка монотонно зменшується від 1 при a = 0 до 0 при  (вторинні джерела не випромінюють у зворотному напрямку).Результуюча амплітуда тепер може бути записана так
(вторинні джерела не випромінюють у зворотному напрямку).Результуюча амплітуда тепер може бути записана так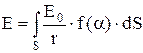 , (2)
, (2) від вторинних джерел випромінювання хвильової поверхні S (сфера радіуса R) у точці М для точкового джерела S0, поверхня S розбивається на кільцеві ділянки радіуса ri, такі, що відстань від суміжних ділянок до точки М різниться на l/2 (див.Мал.14). Це означає, що хвилі від сусідніх ділянок приходять у точку М у протифазі. Амплітуда результуючих коливань у точці М дорівнює
від вторинних джерел випромінювання хвильової поверхні S (сфера радіуса R) у точці М для точкового джерела S0, поверхня S розбивається на кільцеві ділянки радіуса ri, такі, що відстань від суміжних ділянок до точки М різниться на l/2 (див.Мал.14). Це означає, що хвилі від сусідніх ділянок приходять у точку М у протифазі. Амплітуда результуючих коливань у точці М дорівнює , (1)
, (1)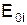 ¾ амплітуда коливань, які збуджуються у точці М і-ю кільцевою поверхнею. Такі кільцеві поверхні називаються зонами Френеля. У
¾ амплітуда коливань, які збуджуються у точці М і-ю кільцевою поверхнею. Такі кільцеві поверхні називаються зонами Френеля. У 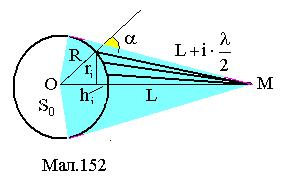 загальному випадку під зонами Френеля розуміють ділянки хвильових поверхонь, для яких відстань від суміжних ділянок до точки М різниться на
загальному випадку під зонами Френеля розуміють ділянки хвильових поверхонь, для яких відстань від суміжних ділянок до точки М різниться на  , а результуюча амплітуда знаходиться алгебраїчним додаванням амплітуд від зон. З малюнка видно, що
, а результуюча амплітуда знаходиться алгебраїчним додаванням амплітуд від зон. З малюнка видно, що . (2)
. (2) . (3)
. (3) , (4)
, (4)
 . (6)
. (6) . (7)
. (7) (5)
(5) .
.


