
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракція Фраунгофера на дифракційній решітці ⇐ ПредыдущаяСтр 6 из 6
а). Розподіл інтенсивності. Дифракційна решіткаутворюється періодичною повторюваністю прозорих (шириною b) та непрозорих плоскопаралельних ділянок (шириною а) на прозорій (наприклад, скляній) поверхні BCG (див.Мал.155). Величина d = b + a (1) називається періодом або сталою решітки. При освітленні решітки світлом, що падає нормально на її поверхню, в напрямку j відбувається інтерференція світла від усіх щілин, із сталою величиною зсуву фаз
Процес інтерференції світла від багатьох прозорих щілин можна описати за допомогою багатопроменевої інтерференції, розглянутої у п.13.8. Результуючу амплітуду можна записати у вигляді
де
У цьому виразі А0 ¾ амплітуда коливань у точці Максимуми виразу (3), що задаються умовою
називаються головними. Амплітуда головного максимуму дорівнює
Якщо з умови головного максимуму підставити
то вираз (3) для амплітуди головного максимуму n-го порядку запишеться у вигляді
Головні максимуми розмежовані між собою мінімумами, які задаються умовою
Таким чином між двома сусідніми головними максимумами знаходяться (N - 1) мінімум та (N - 2) додаткових максимуми. На Мал.156 представлено розподіл головних максимумів при різних значеннях числа щілин N в решітці.
де
Лінійна дисперсія дифракційної решітки за визначенням є
де
і після підстановки
тобто лінійна дисперсія представляється через кутову.
де Величину R можна визначити через параметри решітки за допомогою критерію Релея: дві лінії у спектрі дифракційної решітки будуть розділені, якщо положенню максимуму n-го порядку для
буде відповідати перший мінімум біля максимуму n-го порядку для лінії з
З цього критерію випливає, що
Тепер роздільна здатність запишеться у вгляді R = nN. (16)
|
|||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 239; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.227.69 (0.005 с.) |
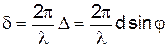 , (2)
, (2) де D ¾ різниця ходу між променями сусідніх прозорих щілин.
де D ¾ різниця ходу між променями сусідніх прозорих щілин. (3)
(3)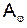 ¾ амплітуда хвилі, що утворюється дифракцією від окремої прозорої щілини в напрямку
¾ амплітуда хвилі, що утворюється дифракцією від окремої прозорої щілини в напрямку 
 . (4)
. (4) , при дифракції від однієї щілини у напрямку
, при дифракції від однієї щілини у напрямку  .
.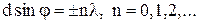 . (5)
. (5) . (6)
. (6) Величина n називається порядком головного максимуму. Головні мінімуми задаються виразом
Величина n називається порядком головного максимуму. Головні мінімуми задаються виразом (7)
(7) ,
, . (8)
. (8) . (9)
. (9) b). Дисперсія дифракційної решітки. Кутова дисперсія дифракційної решіткиза визначенням є
b). Дисперсія дифракційної решітки. Кутова дисперсія дифракційної решіткиза визначенням є , (10)
, (10) ¾ кутова відстань між максимумами одного порядку для двох ліній з
¾ кутова відстань між максимумами одного порядку для двох ліній з  (див.Мал.157). З умови
(див.Мал.157). З умови  диференціюванням одержимо вираз
диференціюванням одержимо вираз  . Звідси вираз (10) у вигляді
. Звідси вираз (10) у вигляді . (11)
. (11) , (12)
, (12) є лінійна відстань на екрані чи фотопластинці між максимумами одного порядку для двох ліній з
є лінійна відстань на екрані чи фотопластинці між максимумами одного порядку для двох ліній з  , яка спирається на кут
, яка спирається на кут 
 , (13)
, (13) c). Роздільна здатність дифракційної решітки. Роздільна здатність дифракційної решіткиза визначенням є
c). Роздільна здатність дифракційної решітки. Роздільна здатність дифракційної решіткиза визначенням є , (14)
, (14)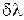 ¾ найменша величина для заданої l, при якій розрізнюються максимуми для довжин хвиль
¾ найменша величина для заданої l, при якій розрізнюються максимуми для довжин хвиль 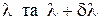 (див.Мал.158).
(див.Мал.158).



 .
.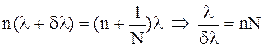 . (15)
. (15)


