
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет операторной передаточной функцииСодержание книги Поиск на нашем сайте
Активного четырехполюсника Выпускаемые промышленностью в виде отдельных микросхем ОУ широко применяются в качестве активных элементов электрических цепей. Условное обозначение ОУ приведено на рис. 8. Входные напряжения
где Параметры современных ОУ во многих случаях допускают их идеализацию. Идеальный ОУ представляет собой источник напряжения, управляемый напряжением, с бесконечно большим коэффициентом усиления ( Анализ цепей, содержащих идеальные ОУ, можно проводить различными методами. Для этого следует воспользоваться схемой замещения ОУ (рис. 9). Ниже рассмотрен пример, в котором расчет цепи четырехполюсника с идеальным ОУ осуществлен методом узловых напряжений.
В примере рассчитывается операторная передаточная функция активного RC -четырехполюсника. Операторная передаточная функция цепи представляет собой отношение операторного изображения реакции (выходного сигнала) к операторному изображению воздействия (входного сигнала). При этом в соответствии с определением цепь должна находиться при нулевых независимых начальных условиях (в данном случае – при нулевых начальных значениях напряжений на емкостных элементах). Пример 1. Рассчитать операторную передаточную функцию активного четырехполюсника, схема которого представлена на рис.10. На основании исходной схемы четырехполюсника составим операторную схему замещения (рис. 11). Для этого пассивные элементы в исходной схеме заменим пассивными двухполюсниками с соответствующими операторными сопротивлениями (резистивному элементу с сопротивлением
Схема четырехполюсника содержит также два идеальных ОУ (DA 1, DA 2). Воспользовавшись схемой замещения идеального ОУ (см. рис. 9) представим тот и другой ОУ в виде управляемых идеальных источников напряжения с операторными ЭДС
К входу четырехполюсника подключим идеальный источник тока, операторное изображение тока которого обозначим Осуществим расчет методом узловых напряжений. Проведем топологический анализ схемы, в ходе которого выявим и пронумеруем узлы. Узел, помеченный знаком общей шины, обозначим как нулевой (узел 0) и примем его за базисный узел. Для операторных изображений узловых напряжений узлов 1–6 введем обозначения К узлам 4, 6 подсоединены выходы ОУ. Узловые напряжения этих узлов являются зависимыми, так как определяются узловыми напряжениями на входах ОУ:
При конечных значениях Таким образом, узловые напряжения узлов, к которым подсоединены инвертирующие входы ОУ, известны – они равны нулю. Неизвестными являются узловые напряжения В матричной форме система узловых уравнений примет вид
Из этой системы линейных уравнений по правилу Крамера могут быть определены операторные изображения узловых напряжений входа и выхода четырехполюсника:
где
Операторная функция передачи рассматриваемого активного четырехполюсника будет равна
После вычисления определителей
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.196 (0.009 с.) |

 ,
,  подаются относительно общей шины, относительно нее снимается и выходное напряжение
подаются относительно общей шины, относительно нее снимается и выходное напряжение  . Один из входов ОУ называется инвертирующим, другой – неинвертирующим. Если при нулевом напряжении на одном из входов ОУ подавать напряжение на другой его вход, то полярность напряжения инвертирующего входа
. Один из входов ОУ называется инвертирующим, другой – неинвертирующим. Если при нулевом напряжении на одном из входов ОУ подавать напряжение на другой его вход, то полярность напряжения инвертирующего входа  ,
, – коэффициент усиления ОУ.
– коэффициент усиления ОУ. ), бесконечными входными (
), бесконечными входными ( ,
, 
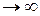 ) и нулевым выходным (
) и нулевым выходным (
 ) сопротивлениями.
) сопротивлениями.

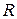 соответствует двухполюсник с операторным сопротивлением
соответствует двухполюсник с операторным сопротивлением 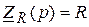 , емкостному с емкостью
, емкостному с емкостью  – двухполюсник с операторным сопротивлением
– двухполюсник с операторным сопротивлением  ).
).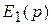 ,
,  .
.

 . Мгновенным значениям входного и выходного напряжений
. Мгновенным значениям входного и выходного напряжений  ,
, 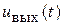 будут отвечать их операторные изображения
будут отвечать их операторные изображения  ,
,  .
. –
–  . При этом отметим, что
. При этом отметим, что  =
=  =
=  =
= 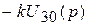 ;
; =
=  .
. имеем
имеем  =0,
=0,  =0. Действительно, инвертирующий вход каждого идеального ОУ виртуально замкнут с его неинвертирующим входом, а напряжения на неинвертирующих входах ОУ в данной схеме, в свою очередь, равны нулю (эти входы соединены с общей шиной).
=0. Действительно, инвертирующий вход каждого идеального ОУ виртуально замкнут с его неинвертирующим входом, а напряжения на неинвертирующих входах ОУ в данной схеме, в свою очередь, равны нулю (эти входы соединены с общей шиной). ,
, 
 =
=  .
. ;
;  ,
, – определитель матрицы узловых операторных проводимостей;
– определитель матрицы узловых операторных проводимостей; =
=  ;
; =
=  .
. =
=  =
=  =
=  .
. ,
,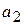 =
= 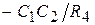 ;
;
 =
=  ;
;
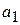 =
=  ;
;
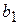 =
= 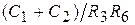 ;
;
 =
= 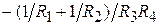 ;
;
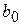 =
=  .
.



