
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внецентренное сжатие стержней.Содержание книги
Поиск на нашем сайте
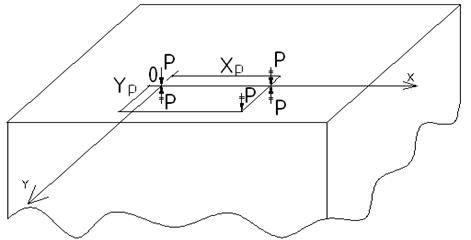
Рассмотрим стержень, подвернутый внецентреному сжатию. Через L обозначаем эксцентриситет приложения сжимающей силы Р. Внецентренно приложенную силу заменяем центрально приложенной силой и изгибающим моментом.
Рассмотрим реальное поперечное сечение стержня:
Рис. 1 Преобразует схему нагружения рассмотренным выше способом. 1)Переносим силу Р на ось ОХ: (у=0) и получаем следующий набор силовых факторов: Р(хр,0), Мх=Рур 2) Переносим силу Р в центральную точку О (0;0) и получаем следующий набор силовых факторов: Р(0;0) - центральная сжимающая сила: Мх=Рур - момент, относительно оси ОХ Му=Рхр - момент, относительно оси OY Запишем формулу для напряжений от действия 3-х выявленных силовых факторов:
Данная формула используется в общем случае внецентренного растяжения и сжатия. Из знаков в формуле (1) в соответствии с конкретикой рис. 1 выбираем знаки “+” или “-“ перед каждым конкретным слагаемым:
Введем понятие о ГОСТотвских величинах радиусов инерции сечения: ix, iy (м)
Возведем формулу (2.1) в квадрат:
Аналогично получаем выражение Перепишем (2) в виде:
Уравнения (2) и (3) представляют собой уравнения плоскости, не проходящей через начало координат, то есть при х=0, у=0 В некоторых случаях данная плоскость делит поперечное сечение на 2 части с разными знаками напряжения:
Rбет сж =30МПа Rбет раст = 0.75МПа Выводим формулу для нулевой линии, на которой напряжения равны нулю, т.е. Из уравнения (3): В общем виде поиск нулевой линии по уравнению (4) сложен. Найдем точку пересечения нулевой линии с осью Х, на которой Y=0:
- найден отрезок, отсекаемый нулевой линией на оси ОХ. Найдем точку пересечения нулевой линии с осью Y, на которой X=0:
- найден отрезок, отсекаемый нулевой линией на оси ОY. Пример: возьмем прямоугольное поперечное сечение
Определяем отрезки, отсекаемые нулевой линией на осях X и Y:
Если сила Р сменит свое положение, передвигаясь к центру тяжести сечения, то зона σ>0 будет прогрессивно убывать. Классифицируем данные случаи: 1. нулевая линия пересекает контур сечения
Рис. 2 В результате в сечении возникают как растягивающие, так и сжимающие напряжения. 2. нулевая линия касается контура сечения, при этом во всем сечении, кроме точки(точек) контура возникают напряжения одного знака.
Рис.3 3. нулевая линия проходит вне контура сечения – во всех точках сечения, включая точки его контура, возникают напряжения одного знака.
Рис. 4 Самым важным является случай 2, т.к. он является предельным для бетона, каменной складки и других материалов, плохо работающих на растяжение. Вводим понятие об ядре сечения (специальной области вокруг центра тяжести сечения) а) если сила Р расположена вне ядра сечения – нулевая линия (н.л.) пересекает контур сечения (рис.2) б) если сила Р расположена на границе ядра сечения- нулевая линия касается контура сечения (рис.3) Т.е. если привести нулевые линии, касающиеся контура сечения, то в этом случае мы найдем точки на границе ядра сечения. Решим задачу:
Рис. 5 І. Н.л. параллельна ОХ:
Перепишем формулы (5) в следующем виде:
ІІ. Н.л. параллельна OY:
Справедлива следующая Теорема: при вращении нулевой линии вокруг некоторой точки соответствующий ей центр давления перемещается по прямой. Рассмотрим вопросы расчетов на прочность. Формула для напряжений при внецентренном сжатии имеет известный вид:
При знании положения н.л. можно выделить две характерные точки поперечного сечения – А и Р.
По закону плоскости максимальное напряжение будет в точке, наиболее удаленной от н.л. Проводим расчет на прочность при сжатии:
Проводим расчет на прочность при растяжении:
Из 2-х значений Р необходимо взять наименьшее, т.к. одновременно должны выполняться оба условия прочности (и на растяжение, и на сжатие). Для построения эпюры нормальных напряжений на контуре поперечного сечения достаточно определить напряжения в точках излома контура и соединить их прямыми линиями, например:
Лекция 19 Косой изгиб Он встречается во многих элементах строительных конструкций.
α- угол между линией действия силы и главной осью балки. Общим является то, что балка изгибается в плоскости, не совпадающей ни с одной из главных осей. Изобразим силу, действующую под углом к главным осям балки.
Рис. 1
Аналогичная ситуация возникает при торможении груза. Ранее изучался изгиб относительно главных осей. Раскладываем силу Р на две составляющие
Ру вызывает изгибание балки относительно оси х:
Аналогично записывается выражение для другой составляющей силы Рх
Суммарное напряжение в точке поперечного сечения:
Знаки в формуле (1) зависят от выбранного напряжения осей х и у.
Очевидно, что в формуле (1) для балки с (рис.2) с нагрузкой с (рис.1) напряжение будет следующим:
Необходимо найти точки сечения, в которых действует наибольшее нормальное напряжение. После этого с использованием условий прочности необходимо подобрать габариты поперечного сечения, а затем определить наибольшие возможные действующие нагрузки, после чего необходимо проверить величины напряжений, действующих в сечении
Как и при внецентренном сжатии точки Из условия
β- угол между нейтральной линией (где Можно записать выражение для
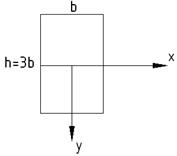
Если Приведем сечения, для которых это выполняется безусловно
Для этих геометрических фигур косой изгиб никогда не реализуется. Косой изгиб реализуется лишь в тех балках, у которых Например, он реализуется для прямоугольного поперечного сечения:
При этом Для доски (прямоугольной) 5х15см Первый вариант существенно экономичней. Наибольшие напряжения возникнут в точках, отмеченных (+)(+) и (-)(-). Определяем напряжения в данных точках:
При косом изгибе главной является проверка на растяжение, т.к., как правило, Вышеприведенное относительно к расчету по первому предельному состоянию (по прочности). Переходим к расчету по второму предельному состоянию (по деформативности). Рассмотрим идеализированный случай прямого изгиба балки.
Определяем прогиб на конце консольной балки. Перемножим эпюры М и М1 по формуле Симпсона.
Переходим к косому изгибу, тогда:
По оси х перемещение вызывается силой
Результирующий вектор прогиба будет определяться по теореме Пифагора:
Подсчитаем угол Запишем: Данная формула совпадает с формулой Отсюда следует, что вектор прогиба перпендикулярен нулевой линии. Для балок различной назначения устанавливается свое собственное отношение Рассмотрим пример по косому изгибу. Зададим пролет двутавровой балки, нагрузку на нее:
Зададим угол отклонения при торможении
Очевидно, что:
Тогда Максимальное напряжение составляем: Сначала подбираем балку при прямом изгибе нос запасом прочность
С запасом принимаем
Проверим данное сечение:
Из-за второй составляющей (горизонтальной) σmax существенно превышает расчетное сопротивление. Предположим, что возьмем наибольший
Тогда: Вывод: сечение необходимо делать из двух прокатных двутавров, так как двутавр Лекция 20
Устойчивость стержней Устойчивость- способность объекта сохранять исходное состояние в равновесии и проектной форме деформирования при действии расчетных нагрузок. Примеры потери устойчивости:
Изогнутое состояние- потеря устойчивости. 41% аварий происходит за счет потери устойчивости элементов конструкции. Теоретически устойчивость стержней исследовал Л. Эйлер (18в.).
Формула Эйлера: Ркрит- номинальная критическая сила, при которой происходит потеря устойчивости стержня.
Формула (1) соответствует шарнирному закреплению стержня по концам.
На практике условие закрепления стержней весьма разнообразное. Поэтому необходимо рассматривать всевозможные варианты. Вводим понятие о приведении длины стержня:
Полуволна синуса набирается на длине При этом формула Эйлера имеет вид:
Рассмотрим самый жесткий, возможный вариант закрепления:
Рассмотрим, что происходит в случае (4), если убрать одну из связей: (горизонтальная подвижность)
Обобщенная формула Эйлера:
Справедливы следующие утверждения: 1) Потеря устойчивости происходит в пределах пропорциональной зависимости между напряжением и деформацией. Формула (3) не применима
2) Сила действует строго центрально 3) Стержень является строго прямолинейным 4) Нет никаких поперечных воздействий на стержень В реальности данное условие не выполняется Рассмотрим случай, когда потеря устойчивости происходит при возникновении пластических деформаций: 1876-1888гг.- США- 251 катастрофа мостов. Слепое следование формуле Эйлера (3) Выясним, к чему ведет ограничение (1):
Переходя от критических сил к критическим напряжениям:
Во внецентренном сжатии введено понятие о радиусе инерции относительно оси:
Тогда:
Вводим понятие о фундаментальной величине- гибкости стержня.
Например, если увеличивается длина стержня, то пропорционально увеличивается его гибкость. При сокращении габаритов поперечного сечения стержня уменьшается Формула для Отсюда находим предельное значение гибкости λ:
Если Для стали:
Для сосны:
Для бетона:
В результате проведения опытов под криволинейными центральносжатыми стержнями, получаются следующие критических напряжений:
Формула для Формула, полученная в результате обработки данных многочисленных опытных исследований, имеет вид:
a и b – экспериментальные коэффициенты (получены статической обработкой данных опытов) Для стали: а=300(МПа); b=1.14(МПа) При подстановке N получаем По Ясинскому: Разделом между формулами является величина
Практический способ расчета стержней на устойчивость: Величина Ркр считается лишь для идеальных стержней: а) идеальный стержень прямолинеен б) центрально-сжатый в) без внутренних полостей г) без боковых воздействий В реальности стержни теряют устойчивость при величинах При этом величина
Общепринято вести расчет следующим образом: Считаем, что Тогда формула принимает следующий вид:
Для каждого материала составляем таблицу в соответствии между гибкостью
Рассмотрим алгоритм использования формулы (9). В нее входят две неизвестных величины А и Тогда
Далее определяем гибкость стержня:
В табличные значения
После этого сопоставим полученные величины
Возвращаемся на подсчет площади поперечного сечения с новым значением
Доказано, что данный процесс сходится к точному значению для конкретного числа шагов. При наличии опыта проектирования конкретных стержней возможно назначать величины
нет: из них следует: Для стальных конструкций Лекция 21
Тонкостенные стержни открытого профиля. Рассмотрим некое тонкостенное поперечное сечение
Считаем, что к тонкостенным профилям относятся такие, у которых:
Например у
У Существуют более сложные тонкостенные поперечные сечения
Рассмотрим особенности работы тонкостенных поперечных сечений:
По (рис.1): Рассмотрим задачу на внецентренное сжатие двутаврового поперечного сечения. Возьмем
Выясним максимальную величину допускаемой силы при приложении ее к точке А1, А2, А3.
Поделим Рдоп при расположении сжимающей силы в точке А3
или:
Эксцентриситет сжимающей силы относительно оси у вызывает резкое снижение величины допустимой нагрузки для двутаврового поперечного сечения. Попытаемся подсчитать координаты пересечения нулевых линий с осями X и Y.
На оси х:
На оси у:
Выясняем, какова будет эпюра напряжений
Полный расчет сжатой стойки предполагает полное исследование ее устойчивости:
Подсчитаем гибкость: Очевидно, что величину критической силы можно определить по формуле Лосинского:
Данная величина меньше, чем Рдоппри простом сжатии без возможности потери устойчивости.
Допускаемое напряжение подсчитывается по формуле:
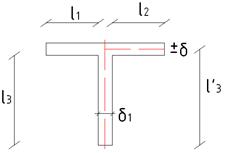
Лекция 22 Расчет изгибаемых балок с тонкостенным поперечным сечением Тонкостенностью называются поперечные сечения, у которых а- длина элемента профиля δ- толщина элемента профиля
Для тонкостенных поперечных сечений дополнительно возникает напряжение:
Причем Сначала необходимо определить все геометрические характеристики поперечных сечений 1) Определение положения центральной точки поперечного сечения: выбираем произвольную ось OY Координаты центральной точки определить по формуле:
Подсчитаем статические моменты площади и площади поперечного сечения:
2) Определяем величины Моментов инерции сечения относительно оси Xc и Yc
Можно построить эпюру у:
Аналогично может быть подсчитана величина Iy:
Статический момент площади: Координаты центра точек:
Итак, выполненные приближенные вычисления обладают высокой точностью. В формуле для моментных напряжений:
Определение: секториальной площадью
Правило №1: в местах соединения элементов профиля
Правило №2: при движении конца вектора по прямой,
При определенном выборе положения полюс эпюра Правило №3: если при движении вектора по прямой треугольники получается вырожденными, то площадь
Для дальнейших вычислений стремимся к наибольшей простой эпюре
Понятие о центре изгиба:
Если равнодействующая, приложенная к нагрузке R, проходящая через центр точки сечения, то создается момент, равный произведению R на решение между центром точки и центром изгиба. В результате поперечное сечение будет закручиваться вокруг центра изгиба, в данном случае по часовой стрелке. Если равнодействующая R действующая в точке изгиба, то сечение деформируется без закручивания и напряжение можно подсчитать по формуле: В реальном случае:
Для получения центра изгиба используется формула:
Тогда
Тогда координата центра изгиба получается по формуле:
Для дальнейших вычислений потребуется эпюра
В формулу напряжения входит секториальная величина для ω:
Лекция 23 Расчет изгибаемых балок с тонкостенным поперечным сечением на стестенное кручение При обычном изгибе балки используется функция у(м)- прогиб у(м) –прогиб
При кручении тонкостенного профиля возникает крутящий момент:
В результате возникает крутящий момент:
Приводим уравнение (1) к виду: Дифференцируем уравнение (1):
Вводим обозначения:
Два начальных параметра определяются сразу из условий на левом конце балки, другой начальный параметр подсчитывается из системы уравнений, записанных для правого конца балки. Нагрузка занимает всю балку целиком. Тогда по методу начальных параметров выражения для функций будут иметь вид:
Все остальные функции получаются дифференцированием приведенного выражения <
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.214.91 (0.015 с.) |


 (1)
(1)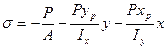 (2)
(2) - радиус инерции сечения относительно оси ОХ (м) (2,1)
- радиус инерции сечения относительно оси ОХ (м) (2,1)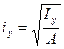 - то же относительно оси OY (2,2)
- то же относительно оси OY (2,2) ,
, (2,3)
(2,3) (2,4)
(2,4)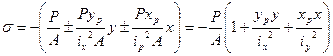 (3)
(3) .
. : хорошо работают практически все материалы.
: хорошо работают практически все материалы. : плохо работает кирпичная кладка и бетон. Например, для бетона класса 30
: плохо работает кирпичная кладка и бетон. Например, для бетона класса 30
 ,
, 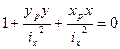 (4)
(4) ,
, 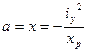 (5,1)
(5,1)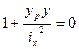 ,
,  (5,2)
(5,2)



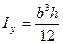

 - на оси OX
- на оси OX - на оси OY
- на оси OY



 ,
, 
 ,
, 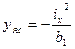
 : точка на границе ядра сечения имеет координату 0 на OY.
: точка на границе ядра сечения имеет координату 0 на OY.
 ,
, 
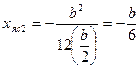
 - на OX
- на OX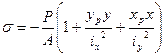



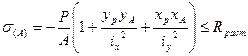
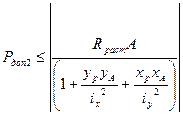


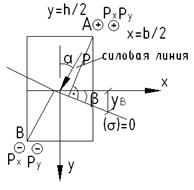

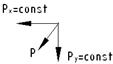

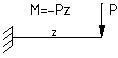 Рис.2
Рис.2
 (1)
(1) - характер изменения изгибающих моментов вдоль оси z.
- характер изменения изгибающих моментов вдоль оси z.
 ;
;  ,
, 

 наиболее удалены от нейтральной линии, на которой
наиболее удалены от нейтральной линии, на которой 

 (2)
(2)
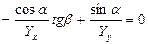

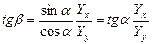
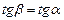 , то силовая линия перпендикулярна нулевой линии.
, то силовая линия перпендикулярна нулевой линии.
 :
: 
 ;
; 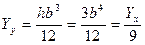

 нулевая линия будет почти горизонтальной.
нулевая линия будет почти горизонтальной.

 .
.


 Относительно оси у прогиб вызывается силой
Относительно оси у прогиб вызывается силой  и составляет
и составляет
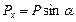 :
:

 , составленный вектором прогиба у:
, составленный вектором прогиба у: (3)
(3)
 , для балок на двух опорах эта величина = 1/450.
, для балок на двух опорах эта величина = 1/450.


 ;
; 

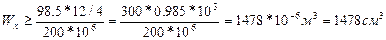
 №55:
№55:





 (1)
(1)

 ,
, 

 - безразмерный коэффициент приведения длины
- безразмерный коэффициент приведения длины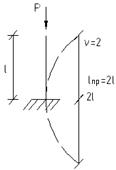

 величины критической силы в 4 раза меньше по отношению к случаю (1).
величины критической силы в 4 раза меньше по отношению к случаю (1).

 с увеличением жесткости опорных устройств величины критических сил возрастают.
с увеличением жесткости опорных устройств величины критических сил возрастают. - длина реализации полуволны синуса.
- длина реализации полуволны синуса.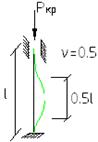
 наивысшее возможное значение критической силы при закреплении стержня по концам.
наивысшее возможное значение критической силы при закреплении стержня по концам.
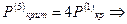 наличие горизонтальных опорных стержней по длине стержня существенно увеличивают величины Ркр.
наличие горизонтальных опорных стержней по длине стержня существенно увеличивают величины Ркр.
 при удалении связи величина критической силы существенно понижается (устойчивость теряется при меньшем значении Ркр).
при удалении связи величина критической силы существенно понижается (устойчивость теряется при меньшем значении Ркр).







 (4)
(4)
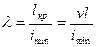 (5)
(5) .
.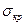 тогда имеет вид:
тогда имеет вид: 
 (6)
(6) , то можно использовать формулу Эйлера:
, то можно использовать формулу Эйлера: ;
;  ;
;
 ;
;  ;
;
 ;
; 


 (7)
(7)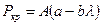

 - формула Эйлера
- формула Эйлера - формула Ясинского
- формула Ясинского
 ,
,  - коэффициент запасоустойчивости
- коэффициент запасоустойчивости

 (8)
(8)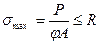
 (9)
(9) и величиной
и величиной 


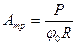

 ,
, 



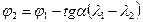
 (10)
(10) . Если они различаются существенно, то:
. Если они различаются существенно, то:
 , которую необходимо округлить до разумной величины. Кроме того, известна величина
, которую необходимо округлить до разумной величины. Кроме того, известна величина  :
: да:
да: 

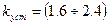
 (i=1,2,…,n)
(i=1,2,…,n)
 - толщина стенки
- толщина стенки - высоко
- высоко
 №40: d=0.8см; h-2t=40-2*1.35=37.3см;
№40: d=0.8см; h-2t=40-2*1.35=37.3см; 




 (Нм2)
(Нм2) ,
,  ,
,  ,
, 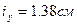

 ;
; 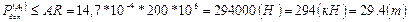

 ;
; 

 ;
; 
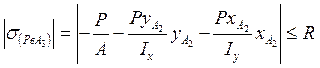


 ;
; 

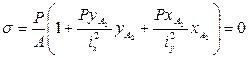 - нулевая линия
- нулевая линия ;
; 


 ;
; 

 в сечении сжатой двутавровой стойки.
в сечении сжатой двутавровой стойки.

 считаем, что потеря устойчивости может произойти в плоскости наибольшей жесткости.
считаем, что потеря устойчивости может произойти в плоскости наибольшей жесткости. ;
;  ;
;  ;
; 




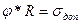

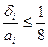

 (1)
(1) вносит существенный вклад в общее напряженное состояние.
вносит существенный вклад в общее напряженное состояние.
 - при этом все размеры берутся в осях элемента.
- при этом все размеры берутся в осях элемента.
 - решение между осью у и центральной точкой сечения.
- решение между осью у и центральной точкой сечения.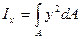
 по формуле Симпсона.
по формуле Симпсона.
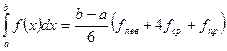 - формула Симпсона
- формула Симпсона

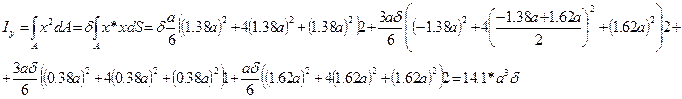 Если использовать для подсчета геометрических характеристик точное выражение, то получаем:
Если использовать для подсчета геометрических характеристик точное выражение, то получаем: . Погрешность в вычислениях:
. Погрешность в вычислениях: 
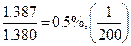
 , погрешность
, погрешность 
 ,
, 
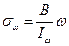
 называется величина, равная удвоенной площади треугольников, описывающих при движении точки по оси элементы сечения.
называется величина, равная удвоенной площади треугольников, описывающих при движении точки по оси элементы сечения.




 меняется по закону прямой линии.
меняется по закону прямой линии.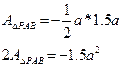





 , причем второе слагаемое вносит существенный вклад в напряженное состояние.
, причем второе слагаемое вносит существенный вклад в напряженное состояние.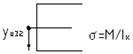
 (2)
(2) - центробежный секториальный момент относительно оси Х.
- центробежный секториальный момент относительно оси Х.
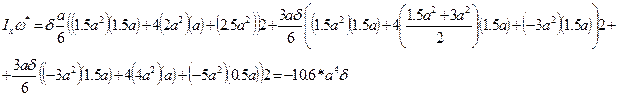
 : в главных центральных осях (Iц) необходимо отстроить по оси ОХ на 0,91.
: в главных центральных осях (Iц) необходимо отстроить по оси ОХ на 0,91. , взятая для полюса в центре изгиба:
, взятая для полюса в центре изгиба:

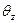 - участок закручивания (рад)
- участок закручивания (рад) - угол поворота
- угол поворота  - искривление поперечного сечения стержня)
- искривление поперечного сечения стержня)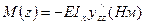 - изгибающий момент
- изгибающий момент  - бимомент
- бимомент
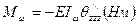 - изгибный момент
- изгибный момент (1) - составляющая крутящего момента
(1) - составляющая крутящего момента

 - расстояние от центра изгиба до центра точки
- расстояние от центра изгиба до центра точки

 - секториальный момент площади при
- секториальный момент площади при  полюсе в центре изгиба.
полюсе в центре изгиба. - погонное колебание
- погонное колебание
 (2)
(2)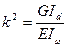 ;
; 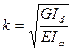 (3)
(3) - может быть решено методом начальных параметров в соответствии с граничными условиями по концам балки.
- может быть решено методом начальных параметров в соответствии с граничными условиями по концам балки.




