
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация граничных условий
Геометрическими, статическими и смешанными.
Граничные условия подразделяют на однородные и неоднородные. Схема подхода к решению задач прочности пластины. 1. Анализ конструкции 2. Расчётная схема 3. Математическая модель 4. Численная реализация матем. модели
Построение аппроксимирующих функций статическим методом В.З.Власова
В.З.Власов (1906-1958гг) предложил способ построения функций распределения прогиба пластины, удовлетворяющих как граничным условиям, так и характеру распределения внешней нагрузки. К входным параметрам относятся: a, b, h (м)-(1,2,3), толщина пластины; E(Па), μ(безр)- (4,5), условие закрепления (6,7,8,9); q(x,y) (10) (при расчете в размерном виде) Σ10
При решении в безразмерном виде решению соответствует бесконечное множество пластин для любых значений а(м), h(м), Е(Па) Далее рассчитываем пластинку в безразмерном виде: По алгоритму статического метода В.З.Власова необходимо: 1.Вырезаем из пластинки полоску по одному направлению 2.Рассматриваем данную полоску как обыкновенную балку
Дифференциальное уравнение изгиба балки имеет вид:
В безразмерном виде: Кроме того используются граничные условия:
Необходимо получить выражение y(η) и для ее производной. Интегрируем выражение (1):
Используем граничные условия для нахождения С1, С2, С3, С4: y(0)=0: 0+0+0+0+С4 =0 => С4=0 yI(0)=0: 0+0+0+C3=0 => C3=0 Используем граничные условия на правом конце балки для подсчета величин С1 и С2:
Подставляя полученные значения:
- точное решение для балки, но приближенное решение для пластинки, по направлению у. Амплитуда прогиба пластинки не связана с амплитудой прогиба балки и затем будет найдена из решения задачи по одному из методов В проведенный характер изменения прогиба пластинки по направлению оси η. Т.е. для дальнейших расчетов применим:
Лекция 28
Построение аппроксимирующих функций статическим методом В.З.Власова Аналогично поступаем по другому направлению:
Записываем дифференциальное уравнение изгиба балки, вырезанной из пластинки:
Граничные условия: х(0)=0, хII(0)=0 Получаем выражение для х(ζ):
Используем граничные условия для нахождения произвольных постоянных интегрирования:
Принимаем для дальнейших расчетов:
Проверяем, удовлетворяет ли функция граничным условиям:
Таким же образом можно проверить функцию у(η):
Надо помнить, что старшая степень х(ζ)=4, т.к. нагрузка ζ и η поставлена. В у(η) старшая степень 5, т.к. нагрузка изменяется линейно.
Рассмотрим пластинку со свободным закреплением края:
Вырезаем из пластинки полоску по направлению оси η. Рассматриваем балку.
Записываем дифференциальное уравнение изгиба балки:
На свободном крае:
Рассмотрим выражение
Записываем функцию прогиба в виде: Производим смягчение граничащих условий по принципу Сен Венона:
Очевидно, что запись примет вид:
Интегрирование идет по ζ, поэтому величины, зависящие от η можно вынести за знак интеграла:
В данном случае у нас X(ζ)- известная функция:
Известно, что В EXCEL подсчет определенных интегралов:
В результате в полученной нами записи оказывается: обозначим
В результате получаем уравнения:
Подставляя сюда выражения для
Аналогично поступаем со вторым граничным условием:
В результате некоторых преобразований получаем:
Дописываем (3) и (4) уравнения в данную систему:
Получаем систему четырех уравнений с четырьмя неизвестными. На главной диагонали должны стоять не нулевые коэффициенты:
Лекция 29
РАСЧЕТ ПЛАСТИН МЕТОДОМ РИТЦА-ТИМОШЕНКО При использовании прямых методов задача, сформулированная в дифференциальных уравнениях, сразу сводится к системе алгебраических уравнений. Если задана функция у(х).
δ- бесконечно малая.
Т. Лагранжа- Лежен- Дирихле: устойчивому состоянию упругой системы соответствует минимуму ее полной потраченной энергии.
Полная потраченная энергия системы вычисляется по формуле: Э=А-U (1) Где А – работа внешней нагрузки, U- работа внутренних усилий. ! Перемещение совпадает с направление силы U: сила совершает работу на перемещение, противоположное их направлению.
Для А и U имеются формулы для балок, пластинок и оболочек. Для пластинок:
Если q(x,y)=q(x)q(y) – разделения переменных
Где, В- искомая амплитуда прогиба, Х(х), Y(y)- аппроксимирование функции по каждому их направлению. Если переменная разделяется функцией q и функцией W. Для пластинок работы внутренних усилий равна: Где Если W(x,y) можно принять в виде (2), то:
Вычитаем вариацию от полной потенциальной энергии:
С точности до бесконечно малых высшего порядка вариации функций равно первому дифференциалу:
В - может меняться, Х(х), Y(y)- фиксированные функции, соответствующие граничным условия и нагружению. Вычисляя данную производную, можно записать:
В результате получается линейное алгебраическое уравнение:
Тогда: Предполагается, что задача будет решиться в безразмерном виде.
По методу Ритца-Тимошенко, основанного на т. Лагранжа- Лежен- Дирихле, необходимо задать функцию прогиба в виде:
Строим аппроксимированную функцию х(ζ): вырезаем полоску по направлению рассматриваемой оси ζ, рассматриваем ее как обыкновенную балку:
Аналогично строим аппроксимированную функцию у(η):
Данным граничным условиям должна удовлетворять функция
Подставляем выражение для Qη После этого выражение для прогиба определено с точностью до параметра В.
При решении задачи в безразмерном виде записывают следующее выражение для полной потенциальной энергии пластинки:
Построено статическим методом В.З. Власова. Тогда величины определенных интегралов:
Вычисляем величины определенных интегралов, входящий в вр.
В результате выражения для
Далее зале записываются выражения:
Тогда прогиб окончательно принимает вид:
Затем необходимо записать в безразмерном виде выражения для изгибаемых моментов и поперечных сил:
Выражения для поперечных сил:
Рассмотрим некоторые вопросы, связанные с очертанием эпюр в пластинках. По заданию на расчет пластинок строят необходимо следующее:
Необходимо сделать следующее: Вводим:
WRITE (‘B=’); READLN (B); 1: WRITE (‘KCI=’); READLN (KCI); WRITE (‘ETA=’); READLN (ETA); W:=B*(KCI*KCI* KCI* KCI-1.5* KCI* KCI* KCI+0.5* KCI)* (ETA*….); WRITELN(‘W=’,W); GOTO1;
Если прописать в W: Mζ=…, Mη=…, Qζ=…, Qη=… ζ=0; 0.25; 0.5; 0.75; 1 η=… В результате получаются эпюры характерного очертания:
Лекция 30 Расчет пластинок методом Бубнова-Галеркина. Записываем дифференциальное уравнение изгиба элемента пластинки:
Для конкретной задачи записывается по два граничных условия в каждой точке.
Записываем дифференциальное уравнение в безразмерном виде: при этом расчет одной пластины соответствует бесконечному множеству реальных пластин. Вводим безразмерные переменные и функции по следующим формулам:
Подставляя данные формулы в уравнение (1):
Вводим параметр
- дифференциальное уравнение изгиба пластинки в безразмерном виде. При этом пластинка примет вид:
В безразмерном виде формулы для внутренних силовых факторов примут вид:
Для оси η:
В уравнении (2) справа от знака “=”- внешние силы, а слева- внутренние. Принцип Лагранжа: Сумма работ всех внешних и внутренних сил упругой системы на любом возможном и бесконечно малом перемещении равно 0. Возможные перемещения должны быть совместимы с граничными условиями задач. Применяем принцип Лагранжа к уравнению (2). Возможное перемещение обозначим: В методе Бубнова-Галеркина прогиб в первом приближении решения записаться в виде:
А- амплитуда прогиба, максимальное из решения задач по методу Бубнова-Галеркина. Вариации прогиба записываются в виде:
В результате подстановки
Тогда получаем следующие выражения:
Т.к. функции
где После нахождения амплитуды прогиба все величины в пластинке подсчитываются по следующим формулам:
Аналогичные формулы для этих параметров используются методом Рицце - Тимошенко. Рассмотрим пример:
Получаем выражения для следующих производных функций
Подсчитаем интеграл:
Аналогично вычисляются интегралы I1 и I4.
После этого необходимо посмотреть следующие эпюры:
Чтобы не ошибиться, можно использовать ПЭВМ;
Можно записать:
WRITE (‘x=’); READLN (x); WRITE (‘y=’); READLN (y); WRITE (‘A=’); READLN (A); MKS:=-A*((12*x*x-9*x)*(y*y*y+y*…)+MU*…) WRITELN(‘MKS=’,MKS);
Лекция 31
Расчет пластинок методом Власова-Конторовича Рассмотрим конкретную пластинку.
Входные данные: a, b, h, E, μ. Условие закрепления пластинки (4) Условие нагружения q(x,y) – аналогичная функция. Если распределение q(x,y) сложное, то нагрузку следует разложить в ряд и получить решение на каждый член ряда. Затем полученное суммируется. Расчет загружения половины плоскости. По нормам расчет ведется по загружению всей половины и четверти плоскости.
Удобнее решать задачу в безразмерном виде.
Входными параметрами являются:
Условие закрепления (4)
При этом необходимо записать в безразмерном виде дифференциальные уравнения изгиба пластин:
Необходимо записать граничные условия:
Если шарнирное закрепление:
Т.к. сторона шарнирного закрепления
Шарнирное закрепление
В соответствии с методом Власова-Канторовича запишем:
Одну из функций необходимо построить по методу В.З. Власова.
С3=0, С4=0
После этого функция Используем принцип Лагранжа. Сумма работ внешних и внутренних сил упругости системы на любом возможном и бесконечно молом равно 0.
Тогда получим:
Все величины, зависящие от η, могли быть получены из-под значения интеграла:
Т.к. функция
В результате из выражения (4) получается обыкновенное дифференциальное уравнение вида, дающая точное решение.
Если рассмотреть полное дифференциальное обыкновенное уравнение с переменными коэффициентами, то для решения можно использовать метод конечных разностей. Т.к. (5) является неоднородным уравнением, то решение запишется в виде:
Приходим к алгебраическому уравнению (характеристическому):
Решение получается в комплексном виде. Необходимо преобразовать его в вид:
Тогда нужно подсчитать 2 величины:
Тогда решение однородного уравнения запишется в виде:
После этого необходимо частное найти решение уравнения: Т.к. нагрузка по оси η постоянна и
Тогда общее решение: Если реализуется случай Р(η)=η, то
Остается найти произвольную постоянную интегрирования из условия закрепления пластинки по оси η
Получается система 4-х алгебраических уравнений относительно С1, С2, С3, С4, из которых находим эти величины.
Записываем выражение для производной функции у(η)
Лекция 32 Теории пластичности Диаграмма деформирования пластичного материала.
Для расчета стальных конструкций пластичную диаграмму заменяют условной диаграммой Прандтля.
В зависимости от рассматриваемого материала (реального) выбирается та или иная (из условия совпадения теоретического материала данного опыта). Для многих материалов диаграмма деформирования является не линейной.
Поэтому возникает необходимость математическое описание зависимости Существуют апробированные формы:
Коэффициенты подбираются из наилучших соответствий теоретической кривой и опытных результатов.
Вычисляем величину секущего и касательного модулей:
Используем два условия: 1)при
В начальном участке деформирования траектория совпадает с упругой траекторией. Для подсчета второго коэффициента используем условие:
Тогда:
Тогда формула имеет вид:
Теорию пластичности можно построить лишь путем введения определенных гипотез. Вспомним термины, относящиеся к напряженному деформированному состоянию тела:
Среднее нормальное напряжение в данной точке: Для деформированного состояния вводим аналогичные величины:
Средняя линейная деформация в данной точке тела: Теория малых упруго-пластических деформаций А.А. Ильюшина Данная теорема базируется на трех законах: 1)Закон изменения объема тела. Изменен6ие объема происходит по линейному закону в следующем виде:
k - объемный модуль данного материала.
2)Закон изменения формы: Изменение формы определяется дивиаторами напряжения и деформации:
Подобие между напряжениями и деформационными состояниями изменения формы
3)Закон о единой кривой деформирования К простому испытанию относится испытание на растяжение, сжатие, изгиб.
Затем, после получения функции f она применяется для любых типов напряженного состояния тела. Как правило, при использовании теоремы Ильюшина вводят дополнительные упрощающие напряжения. Обычно предполагается Запишем:
Тогда формула следует из второго закона:
Траектория
УРАВНЕНИЕ ИЗГИБА БАЛКИ ИЗ ФИЗИЧЕСКИ НЕЛИНЕЙНОГО МАТЕРИАЛА
Рассмотрим балку из материал с нелинейной зависимостью
По теореме Журавского:
Возникает задача записи выражения для изгибающего момента М(z). При этом используются формулы для:
Для несжимаемого материала Тогда: Для балки при нелинейной зависимости будем иметь:
Выражение деформирования через прогиб балки:
Тогда выражение для момента имеет вид:
Подставляем в данную формулу следующие величины:
Тогда изгибающий момент: Рассмотрим балку прямоугольного поперечного сечения:
Подсчитаем величины:
Тогда выражение для изгибающего момента имеет вид:
Тогда:
Для упругой балки получаем:
Уравнение (1) соответствует уравнению равновесия элемента балки под действием распределенной нагрузки q с учетом нелинейной зависимости деформации. Для конкретизации задачи необходимо задать 1)q(z) 2)граничные условия по концам балки:
Лекция 33
СПОСОБЫ КОНКРЕТНОГО РАСЧЕТА ФИЗИЧЕСКИ НЕЛИНЕЙНЫХ БАЛОК Укажем один из способов решения уравнения изгиба физически-нелинейной балки:
E, m- постоянные
(1)- уравнение равновесия элементарной части балки. Для задания конкретной задачи необходимо задать внешнюю нагрузку на балку и условие закрепления.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 820; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.242.165 (0.349 с.) |
 Граничные условия бывают:
Граничные условия бывают: – геометр. гр. усл.
– геометр. гр. усл. – статич. гр. усл.
– статич. гр. усл.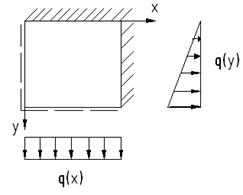

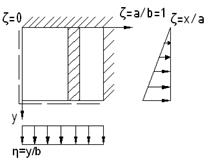


 (1)
(1) ;
; 
 ;
;  ;
; =>
=>  ;
;  ;
;


 ;
; 




 (1)
(1)












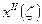 и
и  меняется вдоль свободной стороны
меняется вдоль свободной стороны  , т.е. результат будет разный, если взять ζ=ζ1, ζ=ζ2, ….
, т.е. результат будет разный, если взять ζ=ζ1, ζ=ζ2, …. - запись с разделяющимися переменными, при этом в решении выносится некоторая погрешность.
- запись с разделяющимися переменными, при этом в решении выносится некоторая погрешность. - сумма работ изгибающих моментов на углах поворота вдоль стороны η равно 0. Данная запись следует из вариационной формулировки задачи.
- сумма работ изгибающих моментов на углах поворота вдоль стороны η равно 0. Данная запись следует из вариационной формулировки задачи.
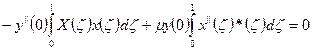
 , поэтому величины определенных интегралов могут быть подсчитаны:
, поэтому величины определенных интегралов могут быть подсчитаны:




 и
и  :
: (1)
(1) - сумма поперечных сил Кирхгофа на прогибы 0
- сумма поперечных сил Кирхгофа на прогибы 0

 (2)
(2)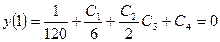 (3)
(3) (4)
(4)
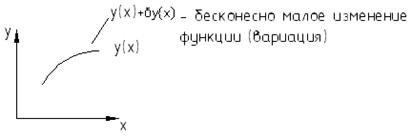




 =>
=>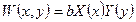 (2)
(2)
 .
.


 - минимальная полная потенциальная энергия
- минимальная полная потенциальная энергия


 -
-



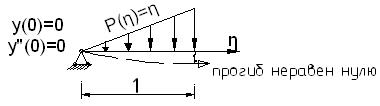





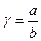 - отношение сторон пластинки
- отношение сторон пластинки




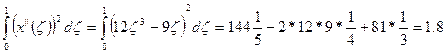


 принимают вид:
принимают вид:


 - амплитуда прогиба пластинки
- амплитуда прогиба пластинки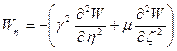



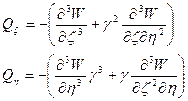
 при
при  ,
, 
 при
при  при
при 

 (1)
(1)
 ,
, 

 - безразмерный параметр прогиба;
- безразмерный параметр прогиба;  - толщина (м).
- толщина (м). ,
, 
 /:
/: 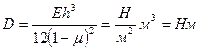




 (2)
(2)

 - безразмерный изгибающий момент в направлении оси ζ.
- безразмерный изгибающий момент в направлении оси ζ. -
-
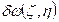 .
.

 - бесконечно малое изменение амплитуды прогиба.
- бесконечно малое изменение амплитуды прогиба. (3)
(3)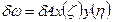 можно записать:
можно записать:

 - функция с разделяющимися переменными
- функция с разделяющимися переменными

 и
и  известны, то известны все величины определенных интегралов. После чего можно записать:
известны, то известны все величины определенных интегралов. После чего можно записать:
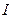 и
и 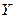 моменты инерции.
моменты инерции.








 в результате вычисления определенных интегралов получаются амплитуды прогибов А.
в результате вычисления определенных интегралов получаются амплитуды прогибов А.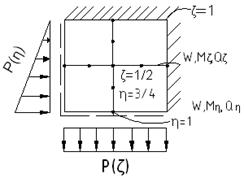




 - функция с разделяющимися переменными
- функция с разделяющимися переменными (1)
(1)
 :
:  ,
,  - жесткое закрепление
- жесткое закрепление :
:  ,
, 
 (2)
(2)
 :
:  ,
,  =>
=> 

 :
: 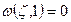 ,
, 
 (3)
(3)
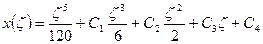

 :
:  заменено приближенным выражением.
заменено приближенным выражением. - приближенное выражение.
- приближенное выражение.
 - малое возмущение
- малое возмущение
 (4)
(4)
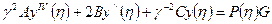 (5)
(5) - решение неоднородного уравнения, определяемое правилом (5) (6)
- решение неоднородного уравнения, определяемое правилом (5) (6) (7)
(7)

 (8)
(8)

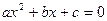
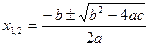 ,
, 


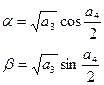



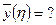
 , то
, то 

 - число
- число



 ,
, 




 ,
,  ,
,  ,
,  ,
, 

 - идеально упругое пластичное тело
- идеально упругое пластичное тело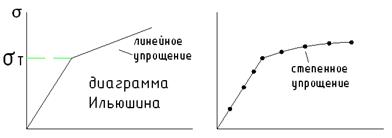

 .
. ,
,  (1) –степенная зависимость с двумя коэффициентами а и k.
(1) –степенная зависимость с двумя коэффициентами а и k. (2) – кубическая парабола
(2) – кубическая парабола (Па)- касательный модуль
(Па)- касательный модуль
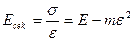


 - начальный модуль материала.
- начальный модуль материала.
 ,
,  , что соответствует точке графика
, что соответствует точке графика 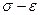

 Па – величины констант получаются в [Па]
Па – величины констант получаются в [Па]


 - тензор напряжения (тензор второго ранга)
- тензор напряжения (тензор второго ранга)



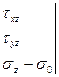




 - тензор деформации (второго ранга)
- тензор деформации (второго ранга)
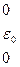



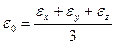
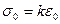

 пропорциональная зависимость между дивиаторами.
пропорциональная зависимость между дивиаторами.


 :
: , причем функция f совпадает стыковой зависимостью
, причем функция f совпадает стыковой зависимостью  при простом испытании материала.
при простом испытании материала.
 , следовательно несжимаем материал (для стержней, пластинок, оболочек значительно легче вызвать изменение формы, чем оббьем)
, следовательно несжимаем материал (для стержней, пластинок, оболочек значительно легче вызвать изменение формы, чем оббьем) ,
,  ,
,  ,
, 
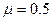 - коэффициент Пуассона для несжимаемого материала.
- коэффициент Пуассона для несжимаемого материала.
 -более простые формулы
-более простые формулы
 и
и  подобны и у них совпадает главные оси.
подобны и у них совпадает главные оси.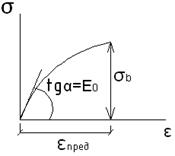
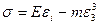 - кубическая парабола
- кубическая парабола



 - нормальное напряжение по продольному направлению вертикального деформирования
- нормальное напряжение по продольному направлению вертикального деформирования ;
; 
 - волокна по высоте балки не давят друг на друга.
- волокна по высоте балки не давят друг на друга. - деформирование по толщине балки
- деформирование по толщине балки - поперечный габарит балки остается постоянным
- поперечный габарит балки остается постоянным


 - для упругой задачи.
- для упругой задачи.
 (совпадает с изменением
(совпадает с изменением 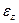 в упругой балке)
в упругой балке)




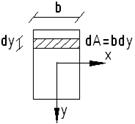

 -момент инерции поперечного сечения
-момент инерции поперечного сечения -геометрическая характеристика высшего порядка
-геометрическая характеристика высшего порядка
 подставим в формулу Журавского:
подставим в формулу Журавского:
 (1)
(1)

 (3)-кубическая парабола
(3)-кубическая парабола ,
, 



