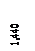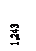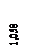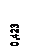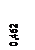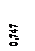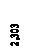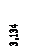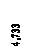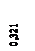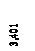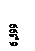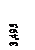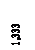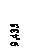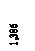Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Из условий закрепления балки по концамСодержание книги
Поиск на нашем сайте
Для того, чтобы построить эпюры прогиба y (Z), углов поворота сечений φ (Z), изгибающих моментов M (Z), поперечных сил Q (Z) по формулам (8), необходимо знать величины начальных параметров y0, φ0, M0, Q0, входящих в (8). Величины двух начальных параметров из четырех непосредственно находятся из условий опирания левого конца балки. Если опирание свободное – рис. 2 а, то M0= 0, Q0= 0, если шарнирное – рис. 2 в, то y0= 0, M0= 0, если левый конец защемлен – рис. 2 д, то y0= 0, φ0= 0. Величины двух других начальных параметров определяются из условий опирания правого конца балки длиной ℓ. Если опирание свободное, рис. 2 б, то для нахождения начальных параметров получаем уравнения М (αℓ) = 0, Q (αℓ) = 0, если шарнирное, рис. 2 г, то уравнения у (αℓ) = 0, М (αℓ) = 0, если правый конец защемлен, рис. 2 д, то уравнения у (αℓ) = 0, φ (αℓ) = 0. Решая систему двух алгебраических уравнений с двумя неизвестными, находим данные параметры. В качестве примера рассмотрим процесс нахождения начальных параметров для балки, изображенной на рис. 6 – свободный от закреплений левый конец балки, шарнирно опертый правый конец балки.
Рис. 6 Балка имеет прямоугольное поперечное сечение b * h = 0,4 * 0,5 м2, модуль упругости бетона берем равным Е = 2,1 * 1010Па, коэффициент жесткости упругого основания К0= 2 * 108н/ м3. В процессе вычислений находим: К = К0b = 2 108 0,4 = 8 * 107н/ м2, Ix= b h3/12 = 0,00416(6) м4, E Ix= 8,76 * 107н/ м2,
Из условий на левом конце балки находим y0= 0, M0= 0. Уравнения для нахождения начальных параметров Q0и φ0будут следующими:
Решая полученную систему уравнений, находим:
Отметим, что в уравнение (8) начальные параметры входят в приведенном виде φ0/α, - M0/(ЕIα2), - Q0/(ЕIα3), поэтому их следует искать в этом же виде, в котором все они имеют размерность длины (м) и характеризуются сопоставимыми между собой значениями. Рассмотрим также пример определения начальных параметров для балки, изображенной на рис. 7 со свободными от закреплений концами.
Рис. 7 Балка имеет прямоугольное поперечное сечение b * h = 0,3 * 0,4 м2, модуль упругости бетона берем равным Е = 2,1 * 1010Па, коэффициент жесткости упругого основания К0= 1 * 108н/ м3. В процессе вычислений находим: К = К0b = 1 108 0,4 = 4 * 107н/ м2, Ix= b h3/12 = 0,0016 м4, E Ix= 3,36 * 107н/ м2,
Из условий на левом конце балки находим M0= 0, Q0= 0. Уравнения для нахождения начальных параметров y0и φ0будут следующими:
Решая полученную систему уравнений, находим:
Отметим, что начальные параметры надо определять с весьма высокой точностью, иначе на правом конце балки значения функций y(L), φ(L), M(L), Q (L) будут содержать заметные погрешности. ПОСТРОЕНИЕ ЭПЮР y (Z), φ (Z), M (Z), Q (Z) И РЕАКТИВНЫХ ДАВЛЕНИЙ R (Z) Изменение напряженно-деформированного состояния балки по ее длине характеризуется эпюрами y (Z), φ (Z), M (Z), Q (Z), то есть графиками изменения этих функций вдоль оси Z. После нахождения приведенных начальных параметров При этом необходимо учитывать правила знаков: прогиб считается положительным, если он совпадает с положительным направлением оси у (вниз), угол поворота сечения φ (Z) считается положительным, если сечение поворачивается по часовой стрелке. Для знаков M (Z) и Q (Z) принимается правило: М>0 в данном сечении балки, если там растянуты нижние волокна и сжаты верхние, Q>0 в данном сечении, если вектор Q стремится повернуть элемент балки по часовой стрелке – рис. 7.
Рис. 8
Эпюра реактивных давлений грунта R(Z) строится на основании формулы (1) после построения эпюры y (Z). В качестве примера рассмотрим процесс построения эпюр для балки, изображенной на рис. 9. Сечение балки – прямоугольное b * h = 0.3 * 0.4 м2, E = 2.1 * 1010Па, K = 6 * 107Па, m = 104нм, Р = 104н, q = 104 н/м. Уравнения для y (Z), φ (Z), M (Z), Q (Z) будут следующими:
Коэффициент
Строим эпюры y (Z), φ (Z), M (Z), Q (Z) для последовательности сечений Z = 0, 0.5, 1.0, 1.5,…, 8, рис. 9. Для проверки правильности построения эпюр можно использовать формулы [1]:
Следует помнить, что первая производная функции в любой точке ее графика равна тангенсу угла наклона касательной в этой точке к оси Z. Таким образом, если при Z2> Z1M2> M1, то на этом участке Q>0, если при Z2> Z1φ2> φ1, то на этом участке M < 0, если при Z2> Z1y2> y1, то на этом участке φ > 0. Например, на рис. 9 при Z < 2 м М возрастает, поэтому Q > 0, при Z > 6 м М убывает, поэтому Q < 0. Отметим также, что если при Z = Zi M = Mэкстр, то в этой точке Q = 0, если при Z = Zi φ = φэкстр, то в этой точке М=0, если при Z = Zi у = yэкстр, то в этой точке φ = 0. Например, на рис. 9 при Z = 2,18 м, 5,37 м, 6,09 м функция прогиба у имеет экстремумы, поэтому в этих точках φ = y ́z= 0. Добавим, что если на балку действуют сосредоточенные силы Рi, то на эпюре Q в этих сечениях должны быть скачки, равные по величине Рiи направленные в сторону действия Рi– сечение Z = 2 м на эпюре Q, рис. 9. Если на балку действуют сосредоточенные моменты mi, то на эпюре М в этих сечениях должны быть скачки, величина которых совпадает с величиной приложенных моментов – например, сечение Z= 6 м эпюры М, рис. 9. P=104 H m=104 Hм
Рис. 9 Лекция 18 СЛОЖНОЕ СОПРОТИВЛЕНИЕ.
|
||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.154.133 (0.008 с.) |




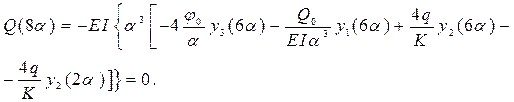
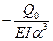 = -2,68324731 * 10-4(м), φ0/α =1,30577156 * 10-4(м).
= -2,68324731 * 10-4(м), φ0/α =1,30577156 * 10-4(м).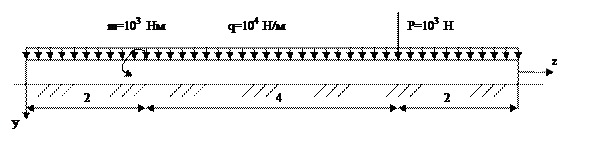
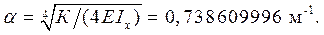


 = 2,56656393 * 10-4(м), φ0/α =-1,47779349 * 10-6(м).
= 2,56656393 * 10-4(м), φ0/α =-1,47779349 * 10-6(м).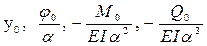 уравнения (8) для y (Z), φ (Z), M (Z), Q (Z) полностью определены и можно строить эпюры.
уравнения (8) для y (Z), φ (Z), M (Z), Q (Z) полностью определены и можно строить эпюры.
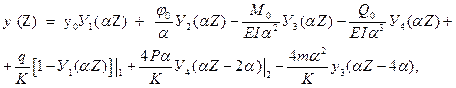
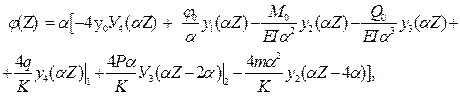 13
13
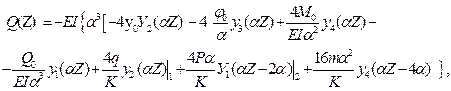
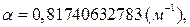 приведенные начальные параметры, найденные из условий закрепления балки по концам, будут:
приведенные начальные параметры, найденные из условий закрепления балки по концам, будут:
 . (12)
. (12)