
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гипотезы сопротивления материалов.Стр 1 из 8Следующая ⇒
1. Принцип относительной жёсткости.
Деформированное состояние (всегда изображается утрированно).
∆<<L, поэтому считаем, что L≈L1 - Ведем расчет по исходной недеформированной схеме.
2. Материал считается сплошным и однородным (можно использовать аппарат дифференциального интегрального исчисления).
3. Материал считается изотропный (св-ва по всем направлениям в точке тела одинаковые).
4. Материал считается упругим (после снятия нагрузки тело полностью восстанавливает свою форму и объём).
5. Линейно-деформируемое тело (пропорциональная связь между нагрузками и перемещениями)
6. Принцип независимости действия силы (принцип суперпозиции).
Эффект от суммы воздействий = сумме эффектов от каждого воздействия в отдельности.
Классификация внешних воздействий и опорных закреплений.
m - сосредоточенный момент, P – сосредоточенная сила.
Момент даст нулевую сумму проекций сил на любую ось. [M]=HM
Интенсивность нагрузки – величина нагрузки, собираемая с одного погонного метра длины стержня. Опорные закрепления.
В жестком защемлении (заделке) присутствуют одновременно три устройства, препятствующие: 1.горизонтальному перемещению стержня в опорном сечении, 2. вертикальному перемещению стержня в опорном сечении, 3. повороту опорного сечения стержня.
Этапы решения инженерных задач. 1. Постановка задачи (Цель исследования)
2. Создание расчетной схемы
3. Математическая модель (задача сводится к системе алгебраических или дифференциальных или интегральных уравнений).
4. Метод решения задачи. 5. Создание алгоритма решения и программы для ПК (желательно использовать готовые программные комплексы). 6. Решение задачи. 7. Инженерное осмысление полученного результата и получение выводов.
Лекция 2 Статическая сторона задачи Основная теорема статического равновесия тел.
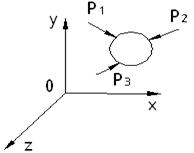
Если тело (часть его) находятся в равновесии, то: 1) Сумма проекций всех активных и реактивных сил на любую ось = 0
2) Сумма моментов всех сил относительно любой оси = 0.
Если рассматривается плоская задача, то
Для решения всех задач обязательно составляются уравнения равновесия. Метод сечений.
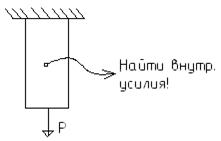
1) Разрезаем (мысленно) стержень некоторым сечением 2) Отбрасываем одну из частей стержня 3) Заменяем действие отброшенной части внутренним продольным усилием N (при растяжении-сжатии стержня) 4) Уравновешиваем оставшуюся часть тела (составляем уравнение(я) равновесия).
Рассмотрим равновесие верхней от сечения части стержня
Нужно рассматривать ту часть стержня, к которой приложено меньше усилий. Правило знаков для продольного усилия N при растяжении- сжатии.
Пример:
Эпюра- график, показывающий изменение некоторой величины вдоль оси стержня. 1) Определим реакцию Va=?
VA>0, следовательно, направление VA выбрано верно. Если VA<0, оставляем направление VA, но считаем её отрицательной величиной. 2) Строим эпюру внутренних продольных усилий N Уч.0-1 0<=y1<=3 - универсальное сечение с текущей координатой РОЗУ
Уч.1-2 0<=y<4 РОЗУ
На эпюре N: 1) Под каждой сосредоточенной силой реализуется скачок на величину данной силы; 2) При отсутствии распределённых по длине нагрузок на каждом i-участке стержня Ni=const
Учет распределённых по длине нагрузок Определить расчетное сопротивление саратовского кирпича
Определена активная нагрузка на стену 1) Определяем опорную реакцию VA=? ∑Fy=0: +VA –qh=0; VA=qh=γAh = H= VA
Уч.0-1 0<=y<=h = 50 (м) 0<=y1<=h РОЗУ
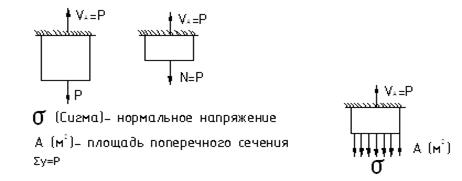
Внутренние напряжения
Вводим гипотезу о равномерном распределении нормальных напряжений в поперечном сечении стержня
Следует помнить, что 1МПа=106Па Условие прочности следующее: |σ|max=|N|max/A <=R, где R - расчетное сопротивление
R=>|N|max/A=|-γAh|/A=γh=2,2*104 (Н/м3)* 50 (м)= 1,1 МПа
С учетом веса перекрытия, покрытия и нагрузки на этажи получается, что сопротивление саратовского кирпича >= 1,5 МПа. Лекция 3 Расчет ступенчатого бруса
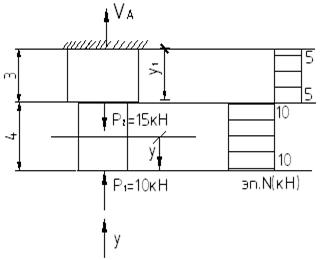
1)VA-? ΣFy=0 +VA-5*3-10*3-15+30=0(кН) VA=15+30+15-30=30(кН) 2)N=? Уч.2-3, 0<=y<=3 РОЗУ
Уч.0-1, 0<=y1<=3 РОЗУ
3)уч.1-2, 3<y1<6 РОЗУ
1) qi=0 Ni=const 2) На участках бруса, где qi= const(i) Ni(y)=ai- qi y - прямая
3) Под каждой сосредоточенной силой (Pi, Vi) реализуется скачок на величину данной силы. 4) Подсчитаем требуемые площади поперечных сечений ступенчатого бруса из условия их прочности σ =N/A |σ i|max=|N i|max/A i<=R=200(МПа) - расчетное сопротивление для стали Ai треб>=|N i|max/R Aтр 0-1>= (30*103(Н))/(200*106(Н/м2))=150*10-6=150/1000000=1,5*10-4=1,5 (см2) Aтр 1-2>=15*103/200*106=0,75*10-4 м2=0,75 см2 Aтр 2-3>=30*103/200*106=1,5 (см2) Строим эпюру нормальных напряжений по длине бруса σi =Ni/Ai На каждом участке стержня необходимо вычислить: σ0=30*103/1,5*10-4=20*107=200*106 Па=200 МПа σ1=15*103/1,5*10-4=100 (МПа) σ1(низ)=15*103/0,75*10-4=200 МПа σ2(верх)= -15*103/0,75*10-4=-200 МПа σ2(низ)= -30*103/1,5*10-4=-200 МПа σ1(верх)= -30*103/1,5*10-4=-200 МПа Итак, на каждом участке бруса эпюра σ подобна эпюре N Строим эпюру продольных перемещений сечений бруса δ (дельта) δ=?
Е- модуль юнга δ 0=0А=0 (заделка в т. А)
δ 1= δ 0+ Δl01= δ0+((N0+N1)/2)l01/EA01=0+((30+15)/2)103*3/(2*1011)*1.5*10-4 = =0+22.5*10-4=2.25*10-3 (м)
δ 2= δ 1+ Δl12=22,5*104+(15-15)*103*3/(2*1011)*0,75*10-4=22,5*10-4=2,25*10-3 (м)
δ 3= δ 2+ Δl23=22,5*10-4+(-30-30)*103*3/(2*1011)*1,5*10-4=22,5*10-4-30*10-4=-7,5 *10-4=-0,7510-3
Определяем δ max в сечении, где N=0 δ max= δ max+ Δl max= 2,25*10-4+((15+0)/2)*103*1.5/2*10110.75*10-4=22.5*10-4+ +7.5*10-4=30*10-4=3*10-3 (м) Итак, на эпюре δ: 1) На участках, где qi=0, δ i(y)=ai+biy -прямая 2) На участках, где qi=const, δ i(y)=ai+biy+ciy2 – парабола второй степени 3) δ i=0 -в заделанном (защемленном) сечении бруса 4) Эпюра δ(y) не имеет разрывов 1 рода (нет скачков на данной эпюре)
Выше было рассмотрена статическая сторона задачи: 1) Уравнения равновесия (ΣFy=0) 2) Внутренняя продольная сила (N(y)) 3) Нормальное напряжение σ=N/A=(Н/м2=Па)
Геометрическая сторона задачи Растяжение и сжатие
Абсолютная величина Δl не характеризует состояние стержня. Вводим понятие о продольной деформации стержня ε (относительной величине) ε= Δl(м)/l(м)= безразмерная величина, которая характеризует состояние стержня в данной его точке Например, для стали ε<=0.0012
Рассмотрим аналогичную задачу для поперечного направления, перпендикулярного действующим продольным силам и получаем абсолютное изменение поперечного габарита стержня Δb=b1-b (1) ε 1= (b1-b)/b= Δb/b (2) - поперечная деформация стержня. Пуассон в 19в. установил: следующий закон связи продольной и поперечной деформаций при растяжении-сжатии стержня ε 1=-µε (3) который гласит: Продольная деформация противоположна по знаку и пропорциональна поперечной деформации. µ (мю)- коэффициент Пуассона, характеризующий свойства материала µсталь=0,3; µбетона=0,1; µжелезобетона=0,15; µ=0,2 (сильно армированный ж/б) Физическая сторона задачи: Ставим в качестве основной задачи нахождение уравнения связи между напряжениями и деформациями. Рассматриваем опытные испытания круглого стального образца из малоуглеродистой стали с площадью поперечного сечения
На участке 0<= σ <= σ n (до предела пропорциональности) напряжения прямо пропорциональны деформациям σ у –предел упругости σy =tg если σ <= σ y, то образец при его разгрузке полностью восстанавливает свои первоначальные форму и объем σ Т –предел текучести материала, при котором происходит перестройка кристаллической структуры материала с образованием неустранимых пластических деформаций.
За площадкой текучести условные напряжения в образце
ε упр - исчезающую упругую деформацию ε пласт – необратимую пластичную деформацию При повторном нагружении образца будет наблюдаться пропорциональная связь между напряжением и деформацией. Т.е. формула (4) справедлива и при разгрузке, и при повторном нагружении за пределами площадки текучести
σ упр=tg α * ε упр, где размерности следующие: Н/м2= (Н/м2)*безр, поэтому в правой части формулы в Н/м2 измеряется важнейшая физическая const материала: МОДУЛЬ ЮНГА: tg α=Е (Па) – модуль Юнга Поэтому в современной редакции закон Гука при растяжении-сжатии имеет вид: σ =Е * ε (5)
Приводим сводку значений модуля Юнга для конструкционных материалов: Е=2,2*1011Па - модуль для стали (1905г) Е=2,1*1011Па - модуль для стали 1935г - (Германия, оболочки покрытия из ж/б) Е=2,06*1011Па - модуль для стали по современному СНиП Е=1,85*1011Па - очень хорошая сталь (мост в Стамбуле через Босфор) Е=2,1*1010Па - 4*1010Па - бетоны различного класса Е=1*1010Па - модуль Юнга для сосны Всегда следует помнить, что Е и µ- 2 основные физические const изотропного материала Задача: Вывести формулу для удлинения стержня при растяжении-сжатии: Δl=?
А- площадь поперечного сечения.
Лекция 4 Рассмотрим конкретный пример расчета стержня
1) VA=?
2) N=? РОЗУ
N(0)= -P=-50 кН N(4)= -50-40= -90 кН СНиП: сталь:
К=1,2.. – коэффициент запаса прочности Расчетное сопротивление для конструкций стали:
Расчет ступенчатого стержня на растяжении и сжатии
Модуль Юнга Е=2*1011Па 1. Определение величины опорной реакции VA=?
2. Строим эпюру продольных усилий N Эп.N=?
РОЗУ
3. Уч.1-2 РОЗУ
4. Уч.0-1
РОЗУ
На эпюре N всегда: 1) На участках без распределений нагрузки (где qi=0) Ni=const 2) На участках с равномерно распределённой нагрузкой qi=const, Ni=ai+-qi*y – прямая 3) Под каждой сосредоточенной силой на эпюре N реализует скачок на величине данной силы (Pj;Vk) 4) Подбираем площади A поперечных сечений стержня из условий их прочности
R- расчетное сопротивление
5.
6. Строим эпюру нормальных напряжений
На каждом участке стержня необходимо рассмотреть 2 крайние точки
Итак, эпюра 7. Строим эпюру вертикальных перемещений сечений бруса
Рассмотрим отдельный случай, когда на участке стержня эп.Nпроходит через 0 график
В сечении, где N=0
8-2x=6x 8=8x x=1
Итак, эп. δ всегда: 1) на участке, где qi=0 2) на участке с распределённой нагрузкой, qi=const -парабола 3) эп. 4) 5) в сечении, где N=0, Лекция 5 Статически определимые и статически неопределимые задачи при растяжении и сжатии В статически определимых задачах неизвестные находят из уравнений статики
1) В статически неопределимых задачах уравнений статики недостаточно для нахождения неизвестных
0=0
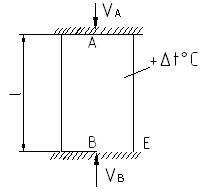
Необходимо записать 2-е уравнение из условия, что длина стержня L=const Рассмотрим температурную статически неопределимую задачу При нагревании стержня он стремится расширится, однако этому препятствуют жесткие (несмещаемые) опоры
(1) Статическая сторона задачи: Составим уравнения равновесия
(2) Геометрическая сторона задачи: l=const, т.е. расстояние между т. А и В остается постоянным Используем метод сечений (РОЗУ) Р азрежем стержень сечением непосредственно у нижней опоры B О тбрасываем нижнюю часть конструкции, т.е. опору В З аменяем отброшенную опору В реакцией VB Составляем уравнение Которое соответствует отсутствию смещения т. В по вертикали:
Для меди Для стали Для бетона Возможность существования ж/б объясняется относительной близостью величин Подставляя полученные слагаемые в выражение для
Рассмотрим конкретные значения:
Итак, при решении задачи использовались: 1.Ур-е равновесия 2.Геометрические уравнения 3.З-н Гука (физическая сторона задачи) Рассмотрим применение данного алгоритма к расчету следующей статически неопределимой системы:
Для составления геометрического уравнения будем считать абсолютно жестким горизонтальный брус, который реально почти не изгибается при нагружении системы. Изображаем деформированное состояние системы
В геометрическое уравнение (2) не входят искомые усилия N1 и N2, поэтому необходимо рассмотрение физической стороны задачи (уравнений закона Гука)
А1=А2=А
Подставляя данные формулы в уравнение (2)
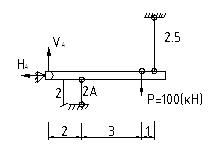
Рассмотрим пример статически неопределимой системы, когда усилие в одном из стержней является отрицательным Вновь считает брус абсолютно жестким.
1) Уравнение статического равновесия
Данная запись необходима для того, чтобы в обоих частях равенства были положительные величины
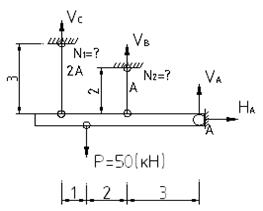
Лекция 6 Рассмотрим полный расчет статически неопределимой системы на растяжение и сжатие
1. Расчет системы по упругой стадии работы подвесок
1) Составляем уравнение статического равновесия: РОЗУ
Получаем одно уравнение с 2-мя неизвестными, т.е. задача является статически неопределимой
2) Геометрическая сторона задачи Абсолютно жесткий брус остается прямолинейным в процессе напряжения системы
3) Рассматриваем физическую сторону задачи
24N1=9N2
Проверка: -6*35-3*13,15=-250 -210-39,45=-205
2.Определяем габариты поперечных сечений стержней подвески Исходные данные: А1=2А, А2=А
1)Составляем величины в стержнях
Выбираем площадь поперечных сечений стержня
Определяем габариты поперечных сечений подвесок (квадрат) А=а2 (круг)
2)Расчет по предельной несущей способности системы Используем идеализированную диаграмму деформированного материала, предложенную одним из создателей теории пластического течения Прандтлем.
возьмем увеличение нагрузки на систему, т.к. Доводим систему до уровня нагружения
Тогда максимально возможное усилие 1-го стержня:
Т.к. при Р1: При Р1<P2: При Р2 =PT система находится в предельном состоянии Определяем величину силы, соответствующей данному предельному состоянию системы
При нагрузке РТ система находится в предельном состоянии, поэтому необходимо ввести коэффициент запаса по несущей способности, для чего можно использовать формулу:
Принимаем коэффициент запаса по несущей способности таким же, как коэффициент запаса по прочности
Р=50кН Сопоставляем величины нагрузок при расчете по упругости стадии работы и возникновении пластичной деформации
Таким образом, при расчете по несущей способности величины расчетных нагрузок на систему могут быть приняты большими, нежели чем при расчете по упругой стадии работы материала, когда достижение расчетного сопротивления в одном (наиболее напряженном стержне) ограничивает дальнейшее увеличение нагрузки на статически неопределимую систему. Учет неточностей монтажа и осадок опор статически неопределимой системы На каждое изделие существуют так называемые допуски и посадки Например, допустимы малые отклонения реальной длины стержня от его проектной длины
Единственный разумный способ монтажа: одновременное перемещение проушины В вниз и проушины С вверх После монтажа система принимает вид: 1)Применяем метод сечений РОЗУ
2)Рассмотрим геометрическую сторону задачи
Необходимо ввести в данное уравнение усилия N1 и N2 , поэтому необходима: 3)Физическая сторона задачи
Подставляя (3) в (2):
N1=N2:
Предположим, что
4)Определяем величины напряжений в стержнях подвесок
Лекция 7 Оптимизация статически неопределимых систем
Основные параметры оптимизации: - стоимость - расход конструкционных материалов - сроки возведения Займемся вопросом о расходе материала
Обеспечиваем равнопрочность стержней 1 и 2
Полученное равенство дает возможность сформулировать условие равнопрочности для статически неопределимых систем: В равнопрочных стержневых системах отношение длины вертикальной подвески к ее расстоянию от шарнирно-неподвижной споры - величина постоянная. Рассмотрим пример системы с несколькими подвесками
Предположим, что система будет равнопрочной, т.е. соблюдается условие Выясним вопрос о возможности повышения несущей способности системы. Предположим, что: в первом стрежне площадь поперечного сечения А1 , а во втором стержне площадь поперечного сечения А2 , а Получим:
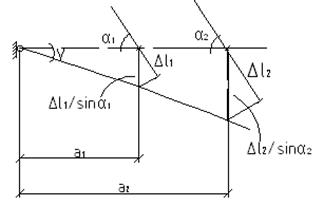
а1нов=2а 1; а2нов=2а2 Pнов= 2P, что дает возможность сделать важный вывод: При пропорциональном увеличении расстояний от стержней подвески до опоры пропорционально растет несущая способность системы. При увеличении плеча одного из стержней несущая способность также возрастает. Расход материала определяется: V= A* l Если стержень с постоянными A и l перемещать вдоль абсолютно жесткого бруса, то объем остается постоянным. Следует добиваться наибольшего плеча силы Pотносительно шарнирно-неподвижной опоры А. Задача:
1) AB = a1*sinα AC = a2*sinα
0 = N1*AB+N2*Al-Pb (І) 2) Геометрическая сторона задачи:
a1*sinα1 = AB = ρ1 a2*sinα2 = AB = ρ2
Полученное равенство дает возможность сформулировать условие равнопрочности для статически неопределимых систем с произвольным углом ориентирования повесок: В равнопрочной статически неопределенной системе отношение длины конкретного стержня к плечу усилия в нем относительно шарнирно-неподвижной опоры – величина постоянная. Лекция 8
Геометрические характеристики плоских сечений Первой геометрической характеристикой является площадь поперечных сечений А (м2). Для вычисления площади необходимо:
Рассмотрим вопрос о площадях и положения центра тяжести элементарных фигур.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.212.145 (0.355 с.) |
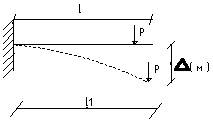


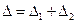



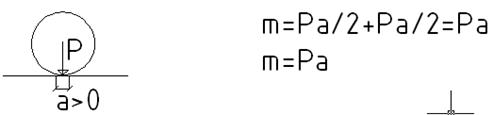



 например, рассчитать надоконную перемычку.
например, рассчитать надоконную перемычку. это упрощённый образ объекта (сохраняет основные, существенные свойства объекта).
это упрощённый образ объекта (сохраняет основные, существенные свойства объекта).




 РОЗУ – аббревиатура метода сечений:
РОЗУ – аббревиатура метода сечений:




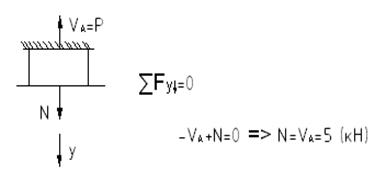


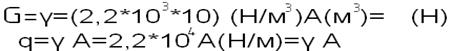

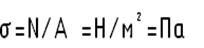


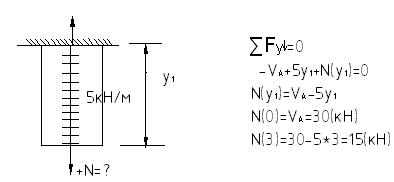





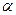 * εy (4)
* εy (4)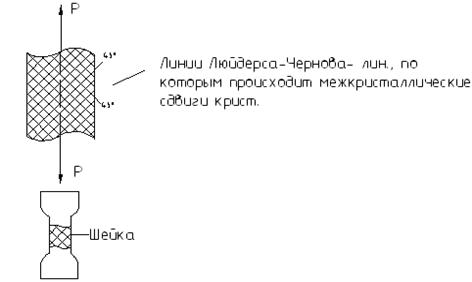
 , где A - первоначальная площадь поперечного сечения образца, вновь возрастают до величины σ в – временного сопротивления. Если разгрузить образец в этой зоне, то имевшаяся у него продольная деформация
, где A - первоначальная площадь поперечного сечения образца, вновь возрастают до величины σ в – временного сопротивления. Если разгрузить образец в этой зоне, то имевшаяся у него продольная деформация  разделится на две части, а именно:
разделится на две части, а именно:

 (6)
(6)
 :
: 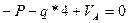




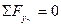 :
: 



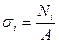 , i – конкретная точка по длине стержня
, i – конкретная точка по длине стержня
 (9) – формула расчета на площадь при растяжении и сжатии
(9) – формула расчета на площадь при растяжении и сжатии
 А=const
А=const




 уч.2-3
уч.2-3








 :
: 






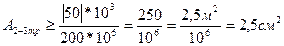



 ; i=1,2,3,…
; i=1,2,3,…



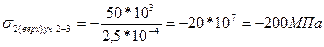
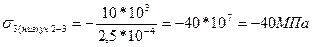
 -при N=const – частный случай
-при N=const – частный случай

 (N– по закону прямых линий)
(N– по закону прямых линий)
 (заделан. сечение)
(заделан. сечение)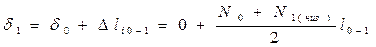


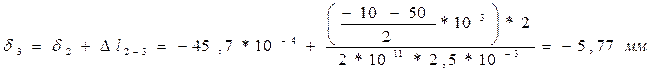

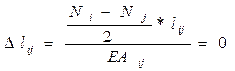






 - прямая
- прямая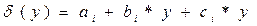
 в заделанном сечении стержня
в заделанном сечении стержня

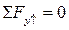


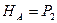

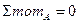
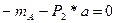


 одно уравнение с 2-мя неизвестными
одно уравнение с 2-мя неизвестными


 - одно уравнение с 2-мя неизвестными
- одно уравнение с 2-мя неизвестными


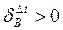 ,
, 


 (1)
(1) -коэффициент температурного расширения конкретного материала (1/град)
-коэффициент температурного расширения конкретного материала (1/град)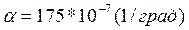


 и получаем
и получаем




 одно уравнение с 2-мя неизвестными
одно уравнение с 2-мя неизвестными

 (2) -геометрическое уравнение
(2) -геометрическое уравнение

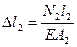 (3)
(3) ,
, 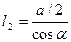




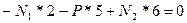 (1)
(1) (2)
(2)
 ,
,  (3)
(3)


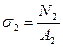 ,
, 

 (1)
(1)
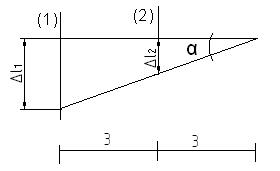
 (2) -геометрическое соотношение неразрывности деформации
(2) -геометрическое соотношение неразрывности деформации -закон Гука
-закон Гука -развернутая формула записи закона Гука при растяжении и сжатии
-развернутая формула записи закона Гука при растяжении и сжатии
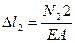

 в уравнение равновесия (1)
в уравнение равновесия (1)
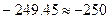




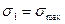







 и
и 
 :
: 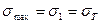 ,
, 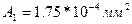









 (1)
(1)
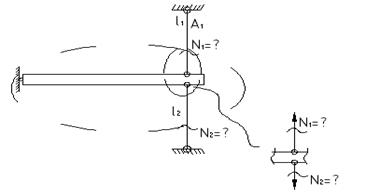


 (2)
(2) ,
, 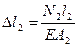 (3)
(3)




 , тогда:
, тогда:
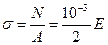


 , поэтому при приложении величины расчетной нагрузки Р к стержню система разрушится, то есть учет неточностей монтажа и осадок опор в статически неопределимых системах необходим.
, поэтому при приложении величины расчетной нагрузки Р к стержню система разрушится, то есть учет неточностей монтажа и осадок опор в статически неопределимых системах необходим.
 (2)
(2) ,
,  :
: 
 (**)
(**) (*)
(*) :
: 
 (1)
(1)
 , тогда
, тогда  ;
; , тогда
, тогда 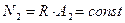
 .
.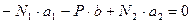

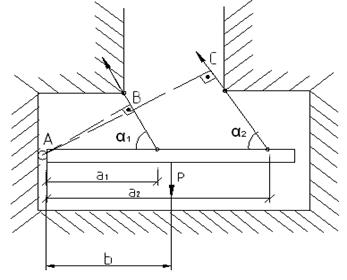
 (І І)
(І І)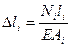 (І І І)
(І І І)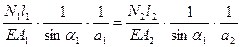
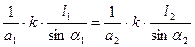
 , где ρ – плечо относительно шарнирно-неподвижной опоры.
, где ρ – плечо относительно шарнирно-неподвижной опоры.
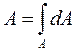 (1) Сложные фигуры можно представить в виде набора треугольников:
(1) Сложные фигуры можно представить в виде набора треугольников:



