Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные геометрические характеристики сечений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для расчета бруса на прочность, жесткость и устойчивость необходимо знать геометрические характеристики его поперечного сечения. Основные геометрические характеристики произвольного плоского поперечного сечения площадью F, представленного на рисунке 1.1, в системе координат XY приведены в таблице 1.1.
Рисунок 1.1 – К определению геометрических характеристик
Таблица 1.1 – Геометрические характеристики плоских сечений
Для расчетов любой конструкции необходимо определять положение центра тяжести ее поперечного сечения. Для сложного или составного сечения общий центр тяжести можно определить по формулам
где n – количество простых фигур, составляющих сечение; Fi – площадь простой фигуры, составляющей сечение; Хi, Уi – координаты центра тяжести простой фигуры в выбранной (начальной) системе координат. Выбор начальной системы координат не влияет на положение центра тяжести составного сечения, а сказывается только на знаках и значениях используемых в расчетах величин. Рекомендуется начало координат размещать в нижнем левом углу сечения или совмещать его с центром тяжести одной из заданных фигур. Следует также обратить внимание на то, что статический момент сохраняет алгебраический знак. Через центр тяжести сечения проходят центральные оси сечения, которые обозначают Х с и У с. Если сечение имеет ось симметрии, то эта ось проходит через центр тяжести и является центральной. Моменты инерции относительно центральных осей обозначают Осевые моменты инерции и полярный момент инерции сечения всегда положительны, а центробежный момент инерции может быть как положительным, отрицательным, так и равняться нулю. Это правило распространяется на большинство простых геометрических фигур (прямоугольник, круг, равнобедренный треугольник и прочие) и на прокатные профили (двутавр, швеллер, уголки). Центробежный момент инерции уголка выбирается по данным сортамента или определяется по формуле
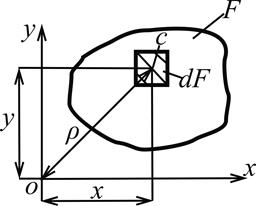
где Imin – минимальный момент инерции уголка. Правило знаков для центробежного момента инерции уголка представлено на рисунке 1.2.
Рисунок 1.2 – Правило знаков центробежного момента инерции уголка
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.226.128 (0.009 с.) |


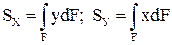
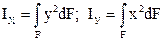
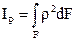


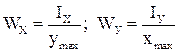

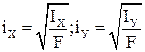
 - расстояния от осей до наиболее удаленных точек сечения,
- расстояния от осей до наиболее удаленных точек сечения, 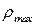 - расстояние от полюса до наиболее удаленной точки сечения.
- расстояние от полюса до наиболее удаленной точки сечения.
 , (1.1)
, (1.1)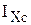 и
и 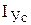 . Статический момент инерции сечения относительно центральных осей инерции равен нулю. Центробежный момент инерции сечений, имеющих хотя бы одну ось симметрии, равен нулю.
. Статический момент инерции сечения относительно центральных осей инерции равен нулю. Центробежный момент инерции сечений, имеющих хотя бы одну ось симметрии, равен нулю.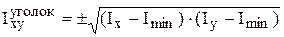 , (1.7)
, (1.7)