
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 14. Определенный интеграл
Задача о вычислении площади криволинейной трапеции. Определенный интеграл как предел интегральной суммы. Формула Ньютона – Лейбница. Свойства определенного интеграла. Вычисление определенного интеграла методом замены переменной и по частям. Понятие о несобственных интегралах с бесконечными пределами интегрирования. Вычисление площадей плоских фигур. Приближенное вычисление определенного интеграла по формуле трапеций ([1 или 6, § 11.1 – 11.8, 11.10]; [2 или 7, § 11.1 – 11.4], или [3, § 11.1 – 11.8, 11.11 – 11.14], или [5, §7.1 – 7.8, 7.11 – 7.14]). Рассматривая задачу о нахождении площади криволинейной трапеции, нужно четко представлять, что сначала выводится формула площади этой фигуры, а затем проводится ее вычисление. Студент должен знать определение определенного интеграла как предела интегральной суммы и то, что благодаря формуле Ньютона – Лейбница ([1, или 6, или 3, формула (11.15)]) – основной формуле интегрального исчисления – удается свести вычисление этого интеграла к нахождению приращения любой первообразной для данной функции на отрезке интегрирования. Следует обратить внимание на достаточное условие интегрируемости функции на данном отрезке – непрерывность функции на этом отрезке. Используя метод подстановки при вычислении определенного интеграла, нужно изменять пределы интегрирования после введения новой переменной и вычислять интеграл, не возвращаясь к старой переменной ([1 или 6, примеры 11.3, 11.18] или [3, примеры 11.3, 11.23]). Применяя формулу интегрирования по частям, можно находить частное приращение первообразной uv в процессе решения, не откладывая это действие до полного отыскания первообразной ([1 или 6, или 3, пример 11.4]). Понятие несобственного интеграла с бесконечными пределами появляется как обобщение понятия определенного интеграла для случая, когда один из пределов интегрирования или оба не ограничены, т.е. когда подынтегральная функция определена и непрерывна на одном из промежутков:
Применяя определенный интеграл для вычисления площадей плоских фигур, мы исходим из того интуитивного утверждения, что всякая плоская фигура, ограниченная несколькими непрерывными кривыми, образующими замкнутый контур, имеет площадь. Следует помнить, что "простейшей" фигурой, площадь которой выражается определенным интегралом, является криволинейная трапеция. Во всех остальных случаях фигуру нужно представить в виде сумм или разностей криволинейных трапеций. Решение задачи на вычисление площади криволинейной трапеции всегда начинают с построения чертежа и при этом следят за тем, чтобы граница фигуры содержала все заданные в условии линии и точки. (Уяснить сказанное можно, разобрав примеры, в которых вычисляются площади различных плоских фигур) (см. ниже, раздел «Задачи для самоподготовки»). Формула трапеций и другие формулы для приближенного вычисления определенных интегралов используются, когда соответствующая первообразная не является элементарной функцией ("неберущийся" неопределенный интеграл) или когда интеграл представляет собой трансцендентную функцию (для составления таблиц значений таких функций).
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.147 (0.004 с.) |
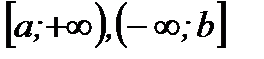 или
или 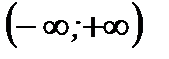 . Если при этом первообразная известна (является элементарной функцией), то сходимость несобственного интеграла устанавливается по определению. Если первообразная неизвестна (неопределенный интеграл не "берется" в элементарных функциях), то сходимость устанавливается косвенным путем с помощью признаков сходимости. Последнее выходит за рамки программы.
. Если при этом первообразная известна (является элементарной функцией), то сходимость несобственного интеграла устанавливается по определению. Если первообразная неизвестна (неопределенный интеграл не "берется" в элементарных функциях), то сходимость устанавливается косвенным путем с помощью признаков сходимости. Последнее выходит за рамки программы.


