
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Векторные пространства
Векторы на плоскости и в пространстве (геометрические векторы). Линейные операции над векторами. Коллинеарные и компланарные векторы. Координаты и длина вектора. Скалярное произведение двух векторов (определение) и его выражение в координатной форме. Угол между векторами. n-мерный вектор. Линейная комбинация, линейная зависимость и независимость векторов. Векторное ( линейное) пространство; его размерность и базис. Разложение вектора по базису. Скалярное произведение векторов в n-мерном пространстве. Евклидово пространство. Длина (норма) вектора. Ортогональные векторы. Ортогональный и ортонормированный базисы. ([1 или 6, § 3.1 – 3.3, 3.5 – 3.8]; [2 или 7, § 3.1 – 3.5], или [3, § 3.1–3.3, 3.5−3.8, 3.10 – 3.14], или [4, § 3.1 – 3.3, 3.6, 3.8, 3.10, 3.11, 3.13, 3.15–3.20]). В школьном курсе математики рассматривалось понятие вектора как направленного отрезка, т.е. множества точек, заключенных между двумя точками прямой с указанным направлением. Там же определялись операции над векторами (сложение, вычитание, умножение вектора на число), вводились координаты и понятие длины вектора. Множества всех плоских и пространственных векторов, для которых определены операции сложения и умножения, а также умножения вектора на число, являются простейшими примерами векторных (линейных) пространств. В данной теме обобщается понятие вектора и дается определение векторного пространства, являющегося основным объектом линейной алгебры. Следует отметить, что понятие линейной комбинации, линейной зависимости и независимости векторов вводится точно так же, как это было сделано в теме 1 для строк (столбцов) матрицы. Обращаем внимание на то, что векторы линейно зависимы тогда и только тогда, когда один из векторов можно представить в виде линейной комбинации остальных векторов. А если среди векторов есть нулевой вектор, то такие векторы всегда линейно зависимы. Нужно четко знать понятие базиса n -мерного пространства, представляющего совокупность его n линейно независимых векторов. При этом любой вектор линейного пространства может быть представлен единственным способом в виде линейной комбинации векторов базиса. Надо уяснить, что, например, три пространственных (два плоских) вектора могут образовать базис, если они некомпланарны (неколлинеарны). Если же они компланарны, т.е. лежат в одной плоскости (коллинеарны, т.е. лежат на одной прямой), то любая их линейная комбинация представляет вектор, лежащий в той же плоскости (на той же прямой), следовательно, по таким векторам не может быть разложен другой вектор, не лежащий в той же плоскости (на той же прямой), а это значит, что компланарные (коллинеарные) векторы базис трехмерного (двумерного) пространства не образуют.
Векторное пространство, как отмечено выше, представляет множество векторов, в которых определены операции сложения векторов и умножения вектора на число, но не определен способ измерения длин векторов и углов между ними. Это становится возможным с введением скалярного произведения векторов и непосредственно связанного с ним понятия евклидова пространства. Скалярное произведение двух векторов надо знать в двух формах (как произведение длин двух векторов на косинус угла между ними и как сумма произведений соответствующих координат (компонент) этих векторов). Обратите внимание на приведенные с решениями задачи [1, или 6, или 3, примеры 3.1– 3.3]. В конце темы вводятся понятия ортогональных векторов. Это позволяет в евклидовом пространстве выделить среди всех базисов ортогональные и ортонормированные базисы, которые более удобны и играют в линейной алгебре роль, аналогичную прямоугольной (декартовой) системе координат в аналитической геометрии (см. тему 6).
Тема 4. Линейные операторы Понятие линейного оператора. Образ и прообраз векторов. Матрица линейного оператора в заданном базисе. Ранг оператора. Операции над линейными операторами. Нулевой и тождественный операторы. Собственные векторы и собственные значения линейного оператора (матрицы). Характеристический многочлен матрицы. Диагональный вид матрицы линейного оператора в базисе, состоящем из его собственных векторов. ([1 или 6, § 3.6, 3.7]; [2 или 7, § 3.3, 3.4], или [3, § 3.6, 3.7, 3.12,3.13], или [4, § 3.8, 3.10, 3.18, 3.19]). . В этой теме рассматривается одно из базовых понятий линейной алгебры – понятие линейного оператора (преобразования, отображения), представляющего закон (правило), по которому каждому вектору х n -мерного пространства
Линейность оператора определяется выполнением свойств аддитивности и однородности оператора [1, или 6, или 3, § 3.6]. Нужно знать, что каждому линейному оператору Особую роль в приложениях линейной алгебры играют векторы, которые под воздействием линейного оператора Если базис линейного оператора составить из собственных векторов, то матрица оператора имеет наиболее простой вид и представляет собой диагональную матрицу, а соответствующая операция называется приведением данной матрицы к диагональному виду ([1, или 6, или 3, пример 3.8]).
Тема 5. Квадратичные формы Квадратичная форма (определение). Матрица квадратичной формы. Матричная форма записи квадратичной формы.. Канонический вид и ранг квадратичной формы. Закон инерции квадратичных форм. Положительно и отрицательно определенная, знакоопределенная квадратичные формы. Критерий определенности квадратичной формы через собственные значения ее матрицы. Критерий Сильвестра. ([1 или 6, § 3.8]; [2 или 7, § 3.5], или [3, § 3.8, 3.14], или [4, § 3.11, 3.13, 3.20]). Квадратичные формы достаточно часто возникают при решении прикладных задач. Если в n -мерном линейном пространстве выбрать некоторый базис, то квадратичную форму Необходимо знать определение и матричную запись квадратичной формы, ее канонический вид. Уметь приводить в простых случаях квадратичную форму к каноническому виду, имея в виду, что это возможно сделать многими способами, но ранг квадратичной формы при этом не меняется. Студент должен владеть двумя способами исследования на знакоопределенность квадратичной формы (с помощью собственных значений ее матрицы и критерия Сильвестра). Например, очевидно, что квадратичная форма
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.156.156 (0.006 с.) |
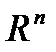 ставится в соответствие один вектор y m -мерного пространства
ставится в соответствие один вектор y m -мерного пространства 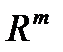 . При
. При 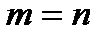 оператор обращает
оператор обращает  соответствует матрица А в некотором базисе
соответствует матрица А в некотором базисе 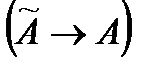 . Верно и обратное утверждение
. Верно и обратное утверждение 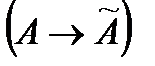 . С помощью этой матрицы для любого вектора х можно найти его образ – вектор y.
. С помощью этой матрицы для любого вектора х можно найти его образ – вектор y.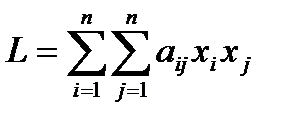 можно рассматривать как некоторую функцию векторного аргумента
можно рассматривать как некоторую функцию векторного аргумента 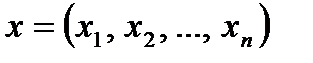 .
.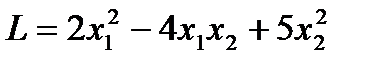 (т.е.
(т.е. 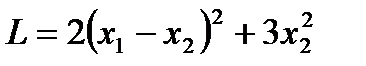 ) является знакоположительной. В этом можно убедиться с помощью отмеченных критериев, ибо матрица квадратичной формы
) является знакоположительной. В этом можно убедиться с помощью отмеченных критериев, ибо матрица квадратичной формы 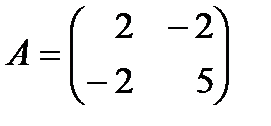 , как нетрудно показать, имеет положительные собственные значения
, как нетрудно показать, имеет положительные собственные значения 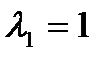 ,
, 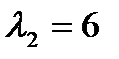 , а угловые (главные) миноры
, а угловые (главные) миноры 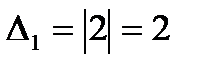 ,
, 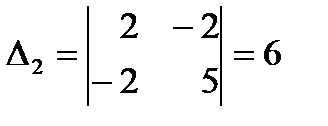 также положительные. А квадратичная форма
также положительные. А квадратичная форма 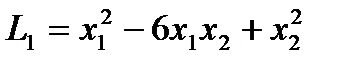 не является знакоопределенной, так как ее матрица
не является знакоопределенной, так как ее матрица 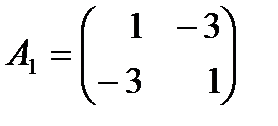 имеет разные по знаку собственные значения
имеет разные по знаку собственные значения 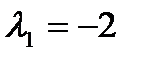 и
и 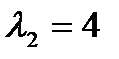 , а угловые миноры
, а угловые миноры 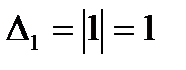 ,
, 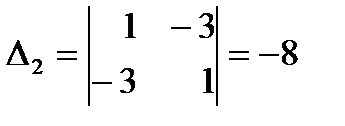 чередуются по знаку, начиная с положительного значения (при
чередуются по знаку, начиная с положительного значения (при 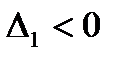 ,
, 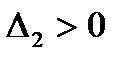 квадратичная форма была бы знакоотрицательной) – (см. [1 или 6, примеры 3.11, 3.12], или [3, примеры 3.11, 3.12, 3.109, 3.110]).
квадратичная форма была бы знакоотрицательной) – (см. [1 или 6, примеры 3.11, 3.12], или [3, примеры 3.11, 3.12, 3.109, 3.110]).


