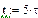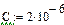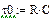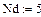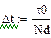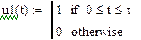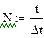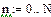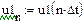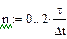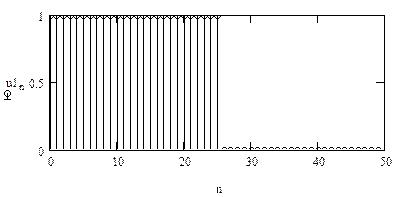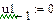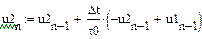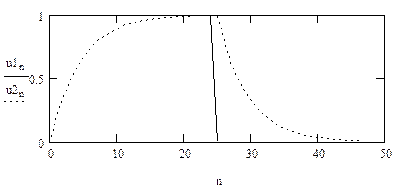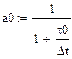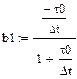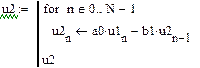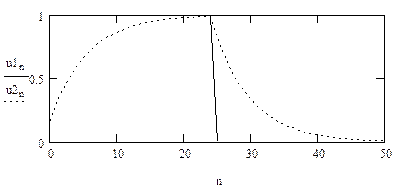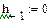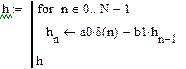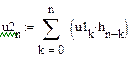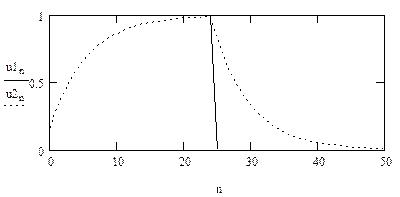Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделювання і аналіз лінійних цифрових фільтрівСодержание книги
Поиск на нашем сайте
Мета роботи – вивчення методів складання і аналізу математичних моделей лінійних цифрових фільтрів.
Теоретичні відомості
Лінійні цифрові фільтри (ЛЦФ) - це лінійні дискретні схеми, призначені для обробки дискретних сигналів в дискретній формі. Модель ЛЦФ може бути представлена у вигляді різністного рівняння або у графічній формі у вигляді структурної схеми. Властивості ЛЦФ можуть бути описані за допомогою передавальної функції, а також за допомогою імпульсної або перехідної характеристик. Різністні рівняння - це аналог диференціальних рівнянь, які є математичними моделями аналогових схем, складених з LCR-елементів. Різницеве рівняння зазвичай отримують шляхом алгебраїзації| диференціального рівняння аналогового прототипу цифрового фільтру. Алгебраїзация - це перетворення диференціального рівняння в рівняння алгебри (різницеве) в результаті застосування того або іншого чисельного методу рішення диференціальних рівнянь. Наприклад, для RC-кола на рис.2.3, що є простим фільтром низьких частот, диференціальне рівняння має наступний вигляд:
де Перетворимо це диференціальне рівняння в різністне, наприклад, за допомогою явного методу Ейлера. Відповідно до цього методу диференціальне рівняння вигляду
приблизно замінюється різницевим рівнянням
Тут використана проста апроксимація похідної кінцевими різницями:
де Перетворивши (6.1) на підставі (6.3), отримаємо різністне рівняння ЛЦФ, відповідне даному RC-колу:
Тут використано позначення: Явний метод Ейлера має обмеження на величину кроку Різністне рівняння повинне бути доповнене початковими умовами. Для рівняння (6.5) початкова умова при нульових початкових умов задається у вигляді Рішення різністних рівнянь виконується рекурсивно, крок за кроком. Наприклад, рішення рівняння (6.5) за нульових початкових умов представляється у вигляді послідовності наступних кроків:
По різницевому рівнянню ЛЦФ можна скласти його структурну схему і, навпаки, по структурній схемі фільтру можна отримати різністне рівняння. При побудові структурних схем ЛЦФ зазвичай використовуються наступні базові елементи:
- суматор
- підсилювач (α>1) або ослаблювач (α<1)
- ланка запізнювання
З використанням даних базових елементів структурна схема ЛЦФ, складена по різністному рівнянню (6.5), має вигляд, показаний на рис. 6.1.
Рисунок 6.1
Для складання передавальних функцій ЛЦФ використовується z-перетворення, що є різновидом дискретного перетворення Лапласа. Передавальна функція ЛЦФ – це відношення z-зображення вихідного сигналу фільтру до z-зображення вхідного сигналу
Для отримання z-зображення до дискретного сигналу
застосовують перетворення Лапласа:
Тут Потім оператора
Відзначимо, що заміна в перетворенні Лапласа комплексної частоти p змінної z, здійснює відображення лівої напівплощини комплексної площини за змінною p у середину круга одиничного радіусу, розташованого в центрі на комплексній площині за змінною z. Ряд (6.7) є ряд Лорана, тому по теоремі Коші формула зворотного z-перетворення набуває наступного вигляду:
Інтеграція тут проводиться по контуру ξ, що охоплює все p полюсів функції Алгоритм аналізу ЛЦФ за допомогою z-перетворення включає наступні етапи.
Тут Z, Z-1 – оператори прямого і зворотного z-перетворення. При складанні передавальної функції
При білінійному перетворенні:
Ці співвідношення отримані в результаті розкладання експоненти у степінний ряд, представлений першими двома членами:
Наприклад, RC-коло на рис. 2.3 з передавальною функцією
у разі лінійного перетворення (6.14) відповідатиме ЛЦФ з передавальною функцією
де По передавальній функції
Цьому рівнянню алгебри з урахуванням теореми запізнювання:
відповідатиме різністне рівняння даного ЛЦФ:
Імпульсна характеристика ЛЦФ визначається по співвідношенню:
Наприклад, імпульсна характеристика ЛЦФ з передавальної функції (6.18) може бути отримана з рішення наступного різністного рівняння:
де По відомій імпульсній характеристиці за допомогою інтеграла згортки обчислюється реакція ЛЦФ на вхідний сигнал
Перехідна характеристика ЛЦФ визначається по співвідношенню:
Тут
Лабораторне завдання 1. Скласти різністне рівняння ЛЦФ по диференціальному рівнянню кола, заданого в лабораторній роботі №2, застосувавши для процедури алгебраізації явний метод Ейлера, формула (6.3). Скласти по різністному рівнянню структурну схему ЛЦФ. 2. Скласти програму і виконати за допомогою різністного рівняння розрахунок реакції ЛЦФ на вхідну дію, задану в лабораторній роботі №1. При рішенні різністного рівняння використовувати нульові початкові умови. Вхідну дію визначити на інтервалі [0, τ]. 3. Скласти передавальну функцію ЛЦФ за передавальною функцією аналогового прототипу фільтру, скориставшись лінійним перетворенням (6.14). 4. Скласти програму і виконати аналіз ЛЦФ методом z-перетворення, формули (6.11) – (6.13) і (6.19) –(6.21). 5. Скласти програму для розрахунку імпульсної характеристики ЛЦФ по співвідношенню (6.22), а також реакції фільтру на вхідну дію методом інтеграла згортки, формула (6.24). При складанні програм аналізу ЛЦФ можна скористатися фрагментами програми моделювання і дослідження реакції цифрового прототипу аналогового RC-фільтру низьких частот (см. рис. 2.3) на вхідну дію у вигляді дискретного сигналу прямокутної форми.
Дискретизація аналогового сигналу
Рішення різністного рівняння, складеного за диференціальним рівнянням аналогового прототипу фільтру
Рішення різністного рівняння, складеного по передавальній функції аналогового прототипу фільтру
Складання імпульсної характеристики і аналіз ЛЦФ методом інтеграла згортки
Зміст звіту 1. Короткі теоретичні відомості, схема ЛЦФ, розрахункові співвідношення, різністни рівняння, передавальні функції. 2. Графіки за результатами розрахунку реакції ЛЦФ на вхідний сигнал по різністному рівнянню, складеному за диференціальним рівнянням аналогового прототипу. 3. Графіки з реакцією ЛЦФ на вхідний сигнал, розрахованої за допомогою різністного рівняння, що складено по передавальній функції аналогового прототипу. 4. Графіки імпульсної характеристики і результати розрахунку реакції ЛЦФ на вхідний сигнал, розрахованої за допомогою інтеграла згортки. 5. Висновки по виконаній роботі.
Контрольні питання 1. Лінійні цифрові фільтри (ЛЦФ). Визначення, способи моделювання і опису їх властивостей. 2. Різницеві рівняння, визначення, способи складання. 3. Приклад складання різницевого рівняння по диференціальному рівнянню. 4. Явний метод Ейлера рішення диференціального рівняння. 5. Вибір кроку рішення по явному методу Ейлера, якщо відома постійна часу RC - або RL – кола. 6. Приклад рішення різницевого рівняння. 7. Елементна база для складання схем ЛЦФ. 8. Приклад складання схеми ЛЦФ. 9. Передавальна функція ЛЦФ, визначення. 10. Методика отримання z-зображення дискретного сигналу. Формула прямого z-перетворення. 11. Методика отримання дискретного сигналу по z-зображенню. Формула зворотного z-перетворення. 12. Алгоритм аналізу ЛЦФ методом z-перетворення. 13. Отримання передавальної функції 14. Отримання передавальної функції 15. Приклад складання 16. Теорема запізнювання для z-перетворення. 17. Імпульсна і одинична ступінчаста функції, їх z-зображення. 18. Зв'язок імпульсної і одиничної ступінчастої функцій з передавальною функцією
Список літературних джерел
1. Корсаков В.В., Крылов С.Я. Основы теории цепей для системотехников.- М.: Высшая школа, 1990. - 224 с. 2. Баскаков С.И. Радиотехнические цепи и сигналы. - М.: Высшая школа, 2000. - 486 с. 3. Зиновьев А.Л., Филиппов Л.И. Введение в теорию сигналов и цепей. - М.: Высшая школа, 1988. - 198 с. 4. Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Высшая школа, 1988. - 394 с. 5. Бобало Ю.А. та інш. Основи радіоелектроніки.: Навчальний посібник. /За ред. Б.А. Мандзія – Львів, В-во НУ «Львівська політехніка», 2002.-.456 с.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.247.221 (0.006 с.) |

 , (6.1)
, (6.1) - вхідний сигнал,
- вхідний сигнал, 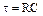 - постійна часу кола.
- постійна часу кола.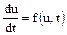 (6.2)
(6.2)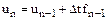 . (6.3)
. (6.3)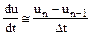 , (6.4)
, (6.4)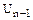 ,
,  – дискретні значення функції для моментів часу
– дискретні значення функції для моментів часу  і
і 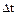 - крок дискретизації. Права частина
- крок дискретизації. Права частина 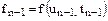 диференціального рівняння (6.2) береться для моменту часу
диференціального рівняння (6.2) береться для моменту часу  .
.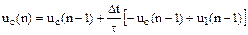 . (6.5)
. (6.5) .
.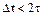 .
. .
. (6.6)
(6.6)
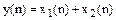 ;
;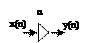
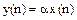 ;
;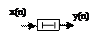
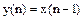 .
.
 :
: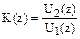 . (6.6)
. (6.6)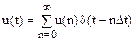 (6.7)
(6.7) . (6.8)
. (6.8)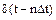 - дельта - функція Дирака.
- дельта - функція Дирака. замінюють оператором z і отримують формулу прямого z-перетворення:
замінюють оператором z і отримують формулу прямого z-перетворення: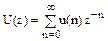 . (6.9)
. (6.9)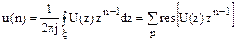 . (6.10)
. (6.10)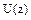 .
.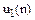 :
: 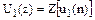 . (6.11)
. (6.11) ЛЦФ.
ЛЦФ. вихідного дискретного сигналу:
вихідного дискретного сигналу: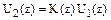 . (6.12)
. (6.12)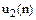 по його z-зображенню
по його z-зображенню 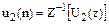 . (6.13)
. (6.13)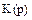 аналогового прототипу використовуються різні апроксимації оператора p оператором
аналогового прототипу використовуються різні апроксимації оператора p оператором 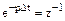 . При лінійному перетворенні має місце наступна апроксимація:
. При лінійному перетворенні має місце наступна апроксимація: . (6.14)
. (6.14)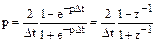 . (6.15)
. (6.15) . (6.16)
. (6.16)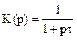 (6.17)
(6.17) , (6.18)
, (6.18)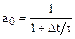 ,
, 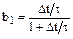 .
. . (6.19)
. (6.19)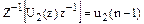 (6.20)
(6.20)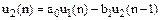 . (6.21)
. (6.21)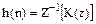 . (6.22)
. (6.22)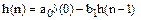 , (6.23)
, (6.23)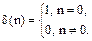
 :
: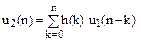 . (6.24)
. (6.24)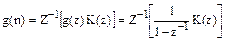 . (6.25)
. (6.25)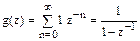 - зображення дискретної одиничної ступінчастої функції.
- зображення дискретної одиничної ступінчастої функції.