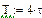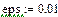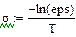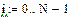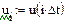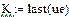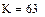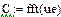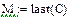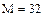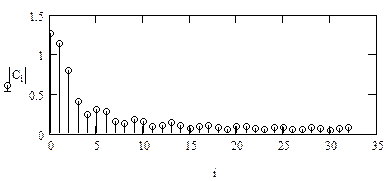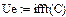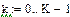Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сигналів на основі швидкого перетворення Фур’єСодержание книги
Поиск на нашем сайте
Мета роботи – вивчення методики застосування швидкого перетворення Фур’є (БПФ) для операторного аналізу сигналів.
Теоретичні відомості
Операторний метод аналізу заснований на аналізі сигналів і лінійних кіл за допомогою інтегральних перетворень Лапласа. Перетворення Лапласа є узагальненням інтегральних перетворень Фур’є і застосовуються для сигналів, визначених для моментів часу, які більше нуля:
де Перетворення Лапласа виходять з перетворень Фур’є при введенні експоненціальної функції, затухаючої на нескінченності:
де у – позитивне число. Для функції (4.2) пряме інтегральне перетворення Фур’є запишеться у вигляді:
де З формули зворотного перетворення Фур’є виходить:
Звідси
Перетворення Лапласа, представлені формулами (4.3), (4.5), можна перетворити у дискретну форму, використовуючи формули (3.6), (3.7) дискретного перетворення Фур’є. З порівняння цих формул витікають співвідношення для дискретного перетворення Лапласа:
де Для розрахунків за формулами (4.6), (4.7) з використанням функцій БПФ fft і ifft слід задати інтервал [0,T] дискретизації сигналу і точність розрахунку ε. За значеннями ε і Т обчислити константу і крок квантування Δt:
де
Лабораторне завдання Скласти програму і виконати за допомогою БПФ операторний аналіз і синтез аналогового імпульсного періодичного сигналу, заданого у лабораторній роботі № 1. Імпульс визначити в інтервалі [0, τ], квантування сигналу в часі здійснити в інтервалі [0,Т ]. У лабораторній роботі потрібно: 1. Визначити по формулі (4.8) постійну загасання σ. 2. Перетворити заданий аналоговий сигнал відповідно до формули (4.2) і представити його в дискретній формі, узявши вибірку об'єму 3. Визначити комплексні амплітуди гармонік спектру перетвореного сигналу за допомогою функції прямого БПФ. Знайти число М гармонік спектру. Побудувати графіки амплитудно- і фазо| - частотного спектру сигналу. 4. Виконати за допомогою функції зворотного БПФ синтез перетвореного сигналу за його спектром. Відновити по формулі (4.6) початковий сигнал за перетвореним. Побудувати на одному полі графіки початкового і синтезованого сигналів. При складанні програми операторного аналізу і синтезу можна скористатися фрагментами програми використання функцій БПФ на прикладі прямокутного імпульсу.
Дискретизація сигналу
Розрахунок спектру перетвореного сигналу
Синтез перетвореного сигналу за його спектром і відновлення форми сигналу
Зміст звіту 1. Короткі теоретичні відомості і розрахункові співвідношення. 2. Графіки початкового і перетвореного сигналів. 3. Графіки з результатами розрахунку амплітуд і фаз гармонік спектру перетвореного сигналу. 4. Графіки початкового і синтезованого сигналів. 5. Висновки по виконаній роботі.
Контрольні питання 1. Для яких сигналів застосовується інтегральне перетворення Лапласа? 2. Визначення одиничної ступінчастої функції (функції Хевісайда). 3. Визначення комплексної частоти. 4. Яке перетворення необхідно здійснити з сигналом, щоб застосувати перетворення Лапласа? 5. Формули прямого і зворотного перетворень Лапласа. 6. Дискретна форма прямого і зворотного перетворень Лапласа на основі дискретного перетворення Фур’є. 7. Як визначити константу у комплексної частоти? 8. Як вибрати число відліків значень сигналу БПФ? 9. Функції прямого і зворотного БПФ, ім'я функцій, розмірності вхідного і вихідного векторів. 10. Як відновити початковий сигнал за наслідками зворотного перетворення Лапласа на основі зворотного БПФ?
Лабораторна робота № 5 Операторний метод аналізу
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.192.214 (0.005 с.) |

 (4.1)
(4.1)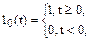 - одинична ступінчаста функція (функція Хевісайда).
- одинична ступінчаста функція (функція Хевісайда). , (4.2)
, (4.2) , (4.3)
, (4.3)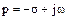 - комплексна частота.
- комплексна частота.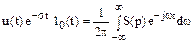 . (4.4)
. (4.4) . (4.5)
. (4.5) , (4.6)
, (4.6)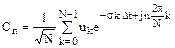 , (4.7)
, (4.7)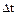 – крок квантування.
– крок квантування.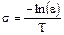 , (4.8)
, (4.8) , (4.9)
, (4.9) , р – ціле число.
, р – ціле число. . Побудувати графіки початкового і перетвореного сигналу.
. Побудувати графіки початкового і перетвореного сигналу.