
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие производной функции.Содержание книги Поиск на нашем сайте
Определение: Производной функции БИЛЕТ 27. Алгебраические свойства дифференцируемых функций. Теорема: Если функции 1) 2) 3) 4)
Доказательство: По теореме об арифметике пределов функций, по определению производной и формулам:
1).
2). = +
3). 4).
БИЛЕТ 28. Дифференцирование сложной функции. Инвариантность формы первого дифференциала.
Производная сложной функции. Пусть функция y=f(x) имеет производную в точке Доказательство: Функция f(x) непрерывна в окрестности точки
F(y)=F(y(x))=Ф(x) и тогда равенство запишем в виде
Инвариантность формы первого дифференциала. Дифференциал первого порядка имеет тот же самый вид: произведение производной функции на дифференциал аргумента, независимо от того, является аргумент независимой переменной или зависимой. z-независимая переменная, y-зависит от x
Если y=f(x), то
БИЛЕТ 29. Теорема Ферма. Теорема Ферма (необходимое условие extr): Пусть
Доказательство. Пусть для определенности в точке
Замечание. Теорема носит локальный характер, т.е. точка
Геометрический смысл теоремы. В предположение теоремы всегда существует точка, в которой касательная к графику функции параллельная OX.
БИЛЕТ 30. Теорема Ролля. Теорема Ролля: Пусть функция y= 1) непрерывна на отрезке [a,b]; 2) дифференцируема (a,b); 3) f(a)=f(b), тогда
Доказательство. Функция f(x), непрерывна на [a,b] достигает на нем max M и min m значения, т.е 1) 2)
Все условия теоремы Ролля существенные. Если выполняется, только 2 из 3(см. картинку), то не существует точка причем БИЛЕТ 31. Теорема Лагранжа (формула конечных приращений).
Теорема Лагранжа. Пусть функция f(x) -непрерывна на отрезке [a,b]; -дифференцируема на интервале (a,b); Тогда
Доказательство. Рассмотрим функцию
Функция F(x) удовлетворяет всем условием т.Ролля (она непрерывна и дифференцируема, как сумма непрерывных и дифференцируемых функций)
Геометрический смысл. В предположение теоремы существует точка
Следствие. Пусть f(x) определена, непрерывна и дифференцируема на (a,b). И в каждой точке интервала (a,b)
Доказательство. Пусть x1 и x2 две произвольные точки интервала(a,b),тогда БИЛЕТ 32. Теорема Коши (обобщенная формула конечных приращений).
Теорема Коши. Пусть функции 1) 2) Доказательство. Рассмотрим функцию
Для функции F(x) выполнены условия теоремы Ролля. Формулировка теоремы Ролля
Следствие. Теорема Лагранжа. Если БИЛЕТ 33. Правила Лопиталя раскрытия неопределенностей.
Правило Лопиталя. Для раскрытия неопределенности вида Доказательство. 1) а - конечное число. Доопределим функции 2) Теорема 2. Пусть Замечание. В формулировке теорем необходимо потребовать, чтобы
Пример, когда нельзя применять правило Лопиталя Вычислим предел отношения производных Вычислить. БИЛЕТ 34. Формула Тейлора. Формула Тейлора. Пусть функция Можно расписать, что
Многочлен
первые равенства получаются путем дифференцирования формулы для Многочлен Обозначим Рассмотрим функцию Т.о получим Пусть функцияf(x) определена на интервале (a,b) и в каждой точке x0 принадлежащей интервалу (a,b) имеем производную до n порядка включительно, тогда
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.185.20 (0.008 с.) |

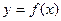 в точке
в точке  называется предел
называется предел 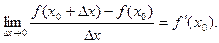 Очень удобна более короткая запись для этого предела и более короткое обозначение для производной
Очень удобна более короткая запись для этого предела и более короткое обозначение для производной  .
. и
и  имеют производные, то
имеют производные, то .
. .
. (
(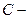 постоянная).
постоянная). .
. ,
,  и
и  имеем:
имеем: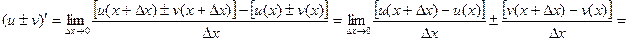

 .
.
 =
=  =
= 
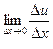 +
+ 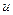
 +
+
 =
= 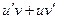 , так как множители
, так как множители  и при
и при  являются постоянными, а
являются постоянными, а  , поскольку
, поскольку  (так как
(так как  ).
). =
= 


 .
. ,а функция z=F(y) имеет производную в точке
,а функция z=F(y) имеет производную в точке  , тогда сложная функция Ф(x)=F(f(x)) имеет производную в точке
, тогда сложная функция Ф(x)=F(f(x)) имеет производную в точке  .
. , поэтому в окрестности точки
, поэтому в окрестности точки 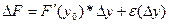 (\/)
(\/) -бесконечно малая более высокого порядка, чем
-бесконечно малая более высокого порядка, чем 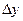 , но
, но  может быть неопределенна в точке
может быть неопределенна в точке  .Разделим равенство (\/) на
.Разделим равенство (\/) на 
 . Перейдем к пределу
. Перейдем к пределу 
 . окажем, что
. окажем, что 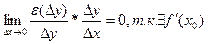 , то y=f(x) непрерывна в окрестности точки
, то y=f(x) непрерывна в окрестности точки  (
(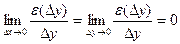 (т.к.
(т.к.  , т.о. получим формулу
, т.о. получим формулу 

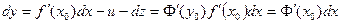

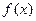 определена на интервале (a,b) и точка
определена на интервале (a,b) и точка 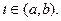 если в точке
если в точке  функция f(x) достигает max или min значения и в точке
функция f(x) достигает max или min значения и в точке  . В точке
. В точке  , тогда
, тогда  (правая и левая производная).Распишем отношение
(правая и левая производная).Распишем отношение
 переходя в этих интервалах к пределу, получим
переходя в этих интервалах к пределу, получим 


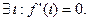
 . Возможны два случая.
. Возможны два случая. и
и 
 ,тогда либо максимальное значение f(x) либо минимальное значения f(x) достигается внутри интервала (a,b) (не на конце отрезка [a,b]).(f(a)=f(b)).
,тогда либо максимальное значение f(x) либо минимальное значения f(x) достигается внутри интервала (a,b) (не на конце отрезка [a,b]).(f(a)=f(b)).  , тогда
, тогда 


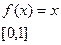


 (касательная параллельная оси ОХ).
(касательная параллельная оси ОХ). (формула конечных приращений)
(формула конечных приращений) .Параметр
.Параметр  выберем из условия F(a)=F(b)
выберем из условия F(a)=F(b)




 :касательная к графику функции параллельна секущей(хорде).
:касательная к графику функции параллельна секущей(хорде).
 , тогда f(x)=const.
, тогда f(x)=const. , точка
, точка  , т.е f(x)=const(в силу произвольности выбора x1 и x2).
, т.е f(x)=const(в силу произвольности выбора x1 и x2). , тогда
, тогда 
 параметр
параметр 

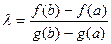 .
. Сравнивания формулы для
Сравнивания формулы для 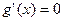 ,то
,то  .
. .Пусть
.Пусть  . И пусть в окрестности точки а существуют
. И пусть в окрестности точки а существуют 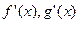 . Если существует
. Если существует  , то
, то  и эти пределы равны.
и эти пределы равны. . Здесь
. Здесь  (использовали теорему Коши). Перейдем к пределу при
(использовали теорему Коши). Перейдем к пределу при 
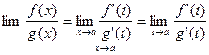 (т.к
(т.к  и если
и если  ).
). надо сделать замену, x=1/t, тогда
надо сделать замену, x=1/t, тогда  ,
, 
 и правило применяется к новой функции
и правило применяется к новой функции 
 .
.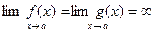 .Если
.Если  , то
, то  -теорема 1 доказана.
-теорема 1 доказана.  -теорема 2 формулировка.
-теорема 2 формулировка.
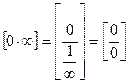
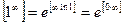
 .
.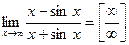 .
. он не существует, т.к. не существует предел числителя и знаменателя. Правило Лопиталя применять нельзя.
он не существует, т.к. не существует предел числителя и знаменателя. Правило Лопиталя применять нельзя.
 , где
, где  -бесконечно малая более высокого порядка чем
-бесконечно малая более высокого порядка чем  , где
, где  линейная функция, причем
линейная функция, причем  .
. , т.е в окрестности точки
, т.е в окрестности точки 
 будем писать в виде
будем писать в виде
 . Вторые равенства - это требуемые свойства
. Вторые равенства - это требуемые свойства  .f(x) у которого существует производная до n порядка включительно можно найти коэффициенты
.f(x) у которого существует производная до n порядка включительно можно найти коэффициенты 
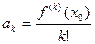 ,
, 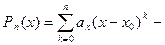 многочлен Тейлора для функции f(x).
многочлен Тейлора для функции f(x).
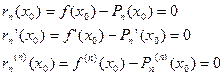
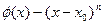 и вычислим
и вычислим 
 ,
,  остаточный член формулы Тейлора.
остаточный член формулы Тейлора.



