Функция, непрерывная на отрезке.

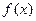Определение: Функция называется непрерывной на отрезке , если она непрерывна в каждой внутренней точке этого отрезка, непрерывна справа в точке 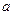и непрерывна слева в точке .

 

Теорема Кантора: Если функция непрерывна на отрезке , то для любого можно указать такое 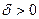, что для любых и из таких, что .

 

+ БОНУС

Доказательство:

Возьмем число . Построим на отрезке точки следующим образом: если точка уже построена, то рассмотрим множество , состоящее из всех точек , удовлетворяющих неравенствам: , .

Положим (см. рисунок), что:

если пусто (и на этом построение заканчивается).

если не пусто.

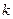Заметим, что в силу непрерывности и для любого из отрезка . Последовательность может быть конечной или бесконечной. Предположим, что она бесконечна, тогда для всех . Пусть . Так как

, то функция непрерывна в точке слева, и потому можно указать такое число

, что и для любого из интервала . По определению числа можно найти в интервале . Тогда любое число из интервала принадлежит интервалу , и потому

, что противоречит тому, что . Таким образом, последовательность не может быть бесконечной, и потому существует такой номер , что . Положим: . Возьмем два любых числа

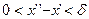и из отрезка таких, что . Тогда возможны два случая: или обе эти точки попали на некоторый отрезок и тогда , или этого не случилось, и тогда найдется точка между и . Но в этом случае , так как и (доказывается аналогично) , а потому . Так как все приведенные рассуждения справедливы для любого , то теорема доказана.

 

Смысл этой теоремы состоит в том, что для всех точек отрезка можно по заданному числу подобрать общее для всех точек число (фигурирующее в определении). Для функций, непрерывных на интервале это можно сделать уже не всегда.

 

БИЛЕТ 26. Дифференцируемость функции. Дифференциал. Понятие производной функ­ции.

Определение: Пусть функция f(x) определена в окрестности точки .Если ее приращение можно представить в виде ,то говорят,что f(x) дифференцируема в точке (иногда пишут -величина более высокого порядка, чем а это означает, что )

-линейная функция от .Она называется дифференциалом функции f(x) и обозначается

 

Пример:

 

Критерий дифференцируемости:

Для того, чтобы функция y=f(x) была дифференцируема в точке необходимо и достаточно, чтобы существовала производная в этой точке.

 

Доказательство:

1.Необходимость. f(x) дифференцируема в точке это означает . Разделим это равенство на и перейдем к пределу ,т.е. существует , т.е. производная существует.

2.Достаточность. Пусть существует или

, т.е. f(x) дифференцируема в точке .

Итак, , т.е. .Отсюда следует новое обозначение производной и эту величину можно рассматривать как один символ, так и как частное дифференциалов.