
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Единственность многочлена Тейлора. ⇐ ПредыдущаяСтр 6 из 6
Пусть функция
Доказательство. Если Пусть
БИЛЕТ 35. Условие постоянства функции. Условие монотонности функции.
На рисунке нарисован график
Теорема (достаточный признак монотонности). 1). Если 2). Если
Доказательство: Возьмем любые числа БИЛЕТ 36. Экстремумы функции. Достаточные условия экстремума. Теорема 1. Необходимое условие экстремума. Пусть точка х0 является точка экстремума для функции f(x). Тогда, если существует f’(x0), то f’(x0)=0, либо f’(x0) не существует.
В точке х1 – min; в точке х2 – max. Теорема 2. Достаточное условие строгого extr в терминах первой производной. Пусть f(x) дифференцируема в некой окрестности точки х0, и в точке х0 f(x) непрерывна. Если f’(x) при переходе через точку х0 меняет знак, то точка х0 является точкой строгого экстремума, при этом 1)если при то в точке х0 – минимум. 2)если при Доказательство. Докажем 1)
2)Доказательство аналогично.
Достаточное условие строгого экстремума в терминах старшей производной. Пусть в точке х0 у функции f(x) существует n производных, причём Следствие. Если в точке х0 у функции f(x) существует Доказательство. Разложим функцию f(x) в ряд Тейлора.
Следствие.
БИЛЕТ 37. Направление выпуклости графика функции. Точки перегиба. Необходимое условие перегиба.
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 836; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.47.221 (0.009 с.) |
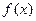 представлена в окрестности точки
представлена в окрестности точки  многочлена вида
многочлена вида 
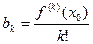
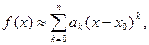 где
где 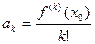 её многочлен Тейлора и есть у нас другой многочлен
её многочлен Тейлора и есть у нас другой многочлен 
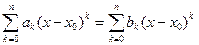 надо показать, что коэффициенты одинаковы
надо показать, что коэффициенты одинаковы 
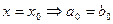 сократим на
сократим на 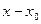
 . пусть
. пусть  сократим на
сократим на 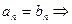 многочлен Тейлора единственен.
многочлен Тейлора единственен.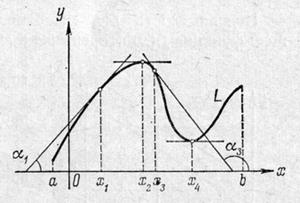
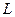 функции
функции 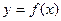 , всюду имеющей производную. В точке
, всюду имеющей производную. В точке 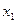 касательная к
касательная к 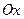 образуют острый угол
образуют острый угол  , поэтому ее угловой коэффициент, равный
, поэтому ее угловой коэффициент, равный  , положителен. Но
, положителен. Но 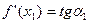 . Следовательно,
. Следовательно, 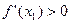 . И так будет в любой точке интервала
. И так будет в любой точке интервала 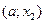 , где функция
, где функция 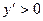 , то на этом интервале функция монотонно возрастает. Далее, в точке
, то на этом интервале функция монотонно возрастает. Далее, в точке 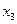 касательная к
касательная к 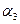 , поэтому ее угловой коэффициент, равный
, поэтому ее угловой коэффициент, равный  отрицателен. А так как
отрицателен. А так как 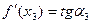 , то
, то 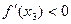 . Вывод: если на интервале
. Вывод: если на интервале 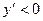 , то на этом интервале функция монотонно убывает. В точке
, то на этом интервале функция монотонно убывает. В точке 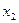 функция имеет максимум. На чертеже ясно, что в этой точке касательная к
функция имеет максимум. На чертеже ясно, что в этой точке касательная к  . При этом слева от этой точки
. При этом слева от этой точки  на отрезке
на отрезке 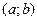 , то
, то 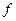 монотонно возрастает на
монотонно возрастает на 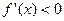 на отрезке
на отрезке 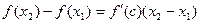 ,
, 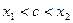 , и поэтому
, и поэтому  принадлежит интервалу
принадлежит интервалу  , то в первом случае
, то в первом случае  , то есть
, то есть 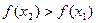 , а во втором
, а во втором 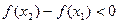 , то есть
, то есть  , что и требовалось доказать.
, что и требовалось доказать.



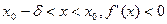 , а при
, а при 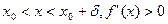
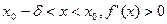 , а при
, а при 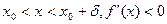 то в точке х0 максимум.
то в точке х0 максимум. .Теорема Лагранжа
.Теорема Лагранжа  . а) Если х-х0>0 и
. а) Если х-х0>0 и  . б) если х-х0<0 и
. б) если х-х0<0 и 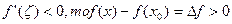 , т.е при переходе через точку х0
, т.е при переходе через точку х0  не меняет свой знак:
не меняет свой знак:  Тогда, если n=2k, то в точке х0 экстремум, и если
Тогда, если n=2k, то в точке х0 экстремум, и если 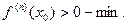
 Если n=2k+1 в точке х0 нет экстремума и точка х0 точка возрастания. Если
Если n=2k+1 в точке х0 нет экстремума и точка х0 точка возрастания. Если 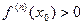
 и точка убывания,
и точка убывания,  если
если 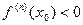 .
.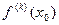 , то, если
, то, если 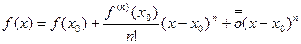 или
или  знак
знак  . По этому, если
. По этому, если  и
и 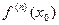 , т.е. при переходе через точку х0 знак
, т.е. при переходе через точку х0 знак  . f’’(x0)>0,
. f’’(x0)>0, 


