
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема: (об отделимости от нуля).Содержание книги Поиск на нашем сайте
Пусть Замечание:
БИЛЕТ 5. Бесконечно малые и ограниченные последовательности. Арифметика бесконечно малых последовательностей. Определение: Последовательность
Теорема: (I)- (II)- (I) (II)
Замечание: Фактически мы дали эквивалентность определений сходящейся последовательности. Определение: Последовательность Замечание: Ранее мы доказали, что всякая сходящаяся, в том числе и бесконечно малая последовательность ограничена.
Арифметика бесконечно малых последовательностей. Теорема: сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность. Пусть
Аналогично
Обозначим Тогда То есть
Теорема: произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
Возьмем произвольный
Обозначим
То есть Замечание: сходимость ограниченной последовательности здесь не требуется.
БИЛЕТ 6. Теорема об арифметике пределов последовательностей.
Пусть 1) существует 2) существует 3) если Доказательства:
1) бесконечно малые.
бесконечно малая бесконечно малая бесконечно малая 3)
По условию
БИЛЕТ 7. Монотонные последовательности. Теорема о пределе монотонной последовательности. Определение:
Теорема (о пределе монотонной последовательности). Пусть
Доказательство:
2) Возьмем произвольный
2)=> Из этого следует, что Мы доказали достаточное условие числовой сходимости последовательности (монот. и огр.)
БИЛЕТ 8. Число е.
Сложно доказать, что функция
Рассмотрим Ограниченность.
+ Монотонность.
+
…
По теореме о монотонности последовательности
БИЛЕТ 9. Подпоследовательности. Частичные пределы. Теорема о частичных пределах сходящейся подпоследовательности.
Определение: Пусть дана некая последовательность
Замечание: Элементы подпоследовательности выбираются в порядке их следования в исходной последовательности.
Определение: Если
Теорема (о частичных пределах сходящейся подпоследовательности): Пусть
Доказательство: Возьмем произвольный Возьмем произвольную
Замечание: Понятие частичных пределов для сходящихся последовательностей не нужно.
БИЛЕТ 10. Теорема Больцано-Вейерштрасса. Теорема: Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 2466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.172.189 (0.005 с.) |


 и
и  . Тогда
. Тогда 
 .
.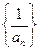 - ограниченная.
- ограниченная.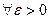


 (
( ).
).




 .
. будем называть бесконечно малой последовательностью, если
будем называть бесконечно малой последовательностью, если  , то есть
, то есть  .
.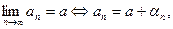
 бесконечно малая последовательность.
бесконечно малая последовательность.

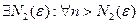
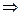 (II)
(II) 

 =
= 

 =
= 
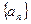 будем называть ограниченной последовательностью, если
будем называть ограниченной последовательностью, если 
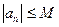 .
.
 . Возьмем произвольный
. Возьмем произвольный  .
.


 .
. .
.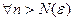
 .
.

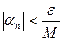 .
. . Тогда
. Тогда .
.
 ,
, 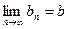 . Тогда:
. Тогда:

 то существует
то существует  .
.
 где
где  - бесконечно малые последовательности.
- бесконечно малые последовательности.
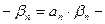 бесконечно малые.
бесконечно малые.

 =
= 
 где
где - бесконечно малая последовательность.
- бесконечно малая последовательность.

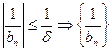 -ограниченная.
-ограниченная. бесконечно малая.
бесконечно малая. (
(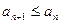 ). Если неравенства строгие, то последовательности строго возрастающие (убывающие).
). Если неравенства строгие, то последовательности строго возрастающие (убывающие). .
.
 .
.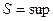

 .
. из 2).
из 2). 1)=>
1)=> 
 (монот. возр).
(монот. возр). =>
=> 
 .
. (огр. на б.м.).
(огр. на б.м.).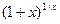 при
при 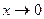 имеет предел. Этот предел обозначается буквой
имеет предел. Этот предел обозначается буквой  в честь открывшего его петербургского математика Леонарда Эйлера. Установлено, что это- иррациональное число и что
в честь открывшего его петербургского математика Леонарда Эйлера. Установлено, что это- иррациональное число и что 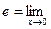
 .
. -биноминальный коэффициент.
-биноминальный коэффициент.


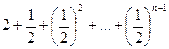 <
< 
 .
.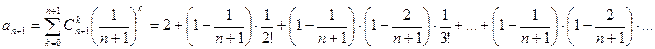


 . Из элементов этой последовательности извлечем другую последовательность
. Из элементов этой последовательности извлечем другую последовательность  , где последовательность
, где последовательность  -номера элементов исходной последовательности, причем
-номера элементов исходной последовательности, причем  Тогда последовательность
Тогда последовательность  - подпоследовательность последовательности
- подпоследовательность последовательности  .
. , то
, то 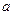 - частичный предел последовательности
- частичный предел последовательности  , тогда
, тогда 
 . Тогда
. Тогда  имеем:
имеем:
 . Таким образом:
. Таким образом:



