Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система автоматизованого моделювання одноелектронних тунельних наносхем simonСодержание книги
Поиск на нашем сайте
Для роботи одноелектронних наносхем повинна бути наявна мінімальна кулонівська електростатична енергія
де Одноелектронні наносхеми містять острівці, що з’єднані у довільному порядку тунельними переходами, конденсаторами та джерелами напруги (рис. 6.1). Джерела напруги мають ідеальні характеристики, тобто їхній внутрішній опір дорівнює нулю. Електрони тунелюють від острівця до острівця через тунельні переходи, змінюючи переміщення зарядів по колу. Щоб забезпечити це, всі опори тунельних переходів мають бути більші за квантовий опір:
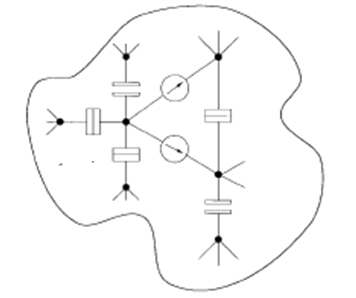
Рис.6.1. Одноелектронне коло з тунельними переходами, конденсаторами та джерелами напруги
Алгоритми моделювання
Існують два основні методи моделювання одноелектронних кіл. Один з них заснований на методі Монте-Карло, а інший — на фундаментальних рівняннях фізики твердого тіла. Метод наближення Монте-Карло починається з розрахунку всіх можливих подій та ймовірностей їх існування, і вибирає одну з можливих подій випадково, відповідно до її ймовірності. Ця операція повторюється багато разів для проведення моделювання переміщень електронів в наносхемі. Події тунелювання розглядаються як незалежні та експоненціально розподілені. З іншого боку, фундаментальні рівняння описують тунелювання електронів між острівцями і, таким чином, наносхема займає різні стани. Один з них є визначальним. Стан визначається напругою джерел живлення та розподілом зарядів між кулонівськими острівцями. Нехтуючи фоновим зарядом, кожний острівець накопичує певну кількість елементарних зарядів. Однак, у випадку постійних джерел напруги стан обчислюється нескінченною кількістю положеннь. У випадку обчислення фундаментальних рівнянь, розглядають обмежену кількість станів. У результаті вирішення знаходять ймовірність стану. У метода Монте-Карло існують наступні переваги: Більш точні імпульсні та динамічні характеристики одноелектронних наносхем тому, що він моделює основу мікроскопічної фізики прямим методом. В реальних одноелектронних колах електрони тунелюють від острівця до острівця так, як це моделюється в методі Монте-Карло. Фундаментальні рівняння використовують наближені величини середніх ймовірностей та коефіцієнтів передачі, які характеризують більш загальну картину. Не потрібно обчислювати початковий стан перед моделюванням, як у випадку з фундаментальними рівняннями. Обчислення більшої кількості початкових станів означає триваліший процес моделювання та зменшену обчислювальну стабільність. Просто змінювати співвідношення між точністю та часом моделювання, тому можна швидко отримати наближені результати моделювання великих наносхем. Щоб підвищити швидкість вирішення фундаментальних рівнянь, слід обмежити кількість обчислених станів. Через відсутність даних про домінуючі стани, суттєве скорочення їх кількості неможливе. Проте у метода Монте-Карло є один великий недолік. При моделюванні співтунелювання через декілька віртуальних переходів простий метод наближення Монте-Карло має обмеження. Співтунелювання — це рідкісний процес і його важко розраховувати за допомогою методу Монте-Карло. Такий розрахунок буде дуже тривалим. Цю проблему вирішують шляхом використання алгоритму, який поєднує в собі обидва методи. Для моделювання будують матрицю ємностей з опису наносхеми:
де Таким чином, відомі тільки частина вузлових напруг та вузлових зарядів. Після того знаходять матрицю, обернену до матриці ємностей, щоб розділити відомі та невідомі змінні:
Для моделювання ефектів тунелювання електронів від острівця до острівця повинні бути визначені темпи всіх можливих випадків тунелювання. Звичайний темп тунелювання для поодинокого тунельного переходу визначається за формулою:
де
з
де Отже всі темпи тунелювання відомо, а дійсні події тунелювання визначаються за методом Монте-Карло. Явища тунелювання визначаються як незалежні і експоненціально розподілені процеси. Комбінування методу Монте-Карло та експоненціального розподілу дає вираз для визначення інтервалів між подіями тунелювання в окремому тунельному переході:
де r – рівномірно розподілене випадкове число на інтервалі [0,1] і Г – це темп тунелювання. Зазвичай вибирається подія з найменшою тривалістю. Після тунелювання заряди вузлів та вузлові напруги змінюються. Таким чином, вільна енергія також змінюється, і темпи розраховуються заново. Цей цикл повторюється багато разів для моделювання переміщення електронів через наносхему. Для одноелектронних схем існує проблема впливу початкового, поляризаційного, фонового заряду. Домішки підкладки та захоплені електрони в речовині індукують заряди на острівці, які зазвичай руйнують функціонування одноелектронних пристроїв. Рівень розвитку технологій на сьогоднішній день не здатний забезпечити достатню чистоту речовини для побудов одноелектронних пристроїв. Один домішковий атом, може повністю змінити всю поведінку пристрою. Розглянемо одноелектронний транзистор (рис. 6.2) при Т=10К, нульовій напрузі на затворі і початковому заряді Qb=0, 0.25q, 0.5q. квантовий острівець
Рис. 6.2. Схема одноелектронного транзистора
На ВАХ (рис. 6.3) спостерігається кулонівська блокада.

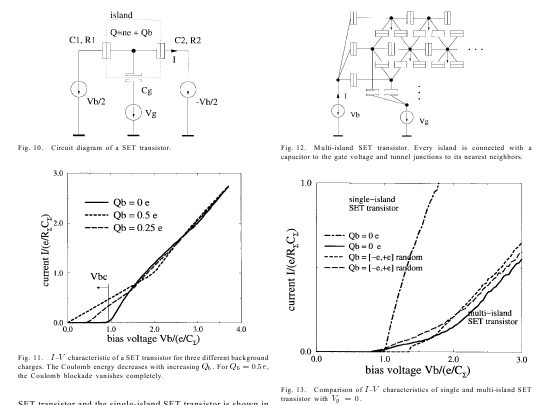
Рис. 6.3. Характеристики одноелектронного транзистора для трьох різних фонових зарядів
Чисельно її величина дорівнює:
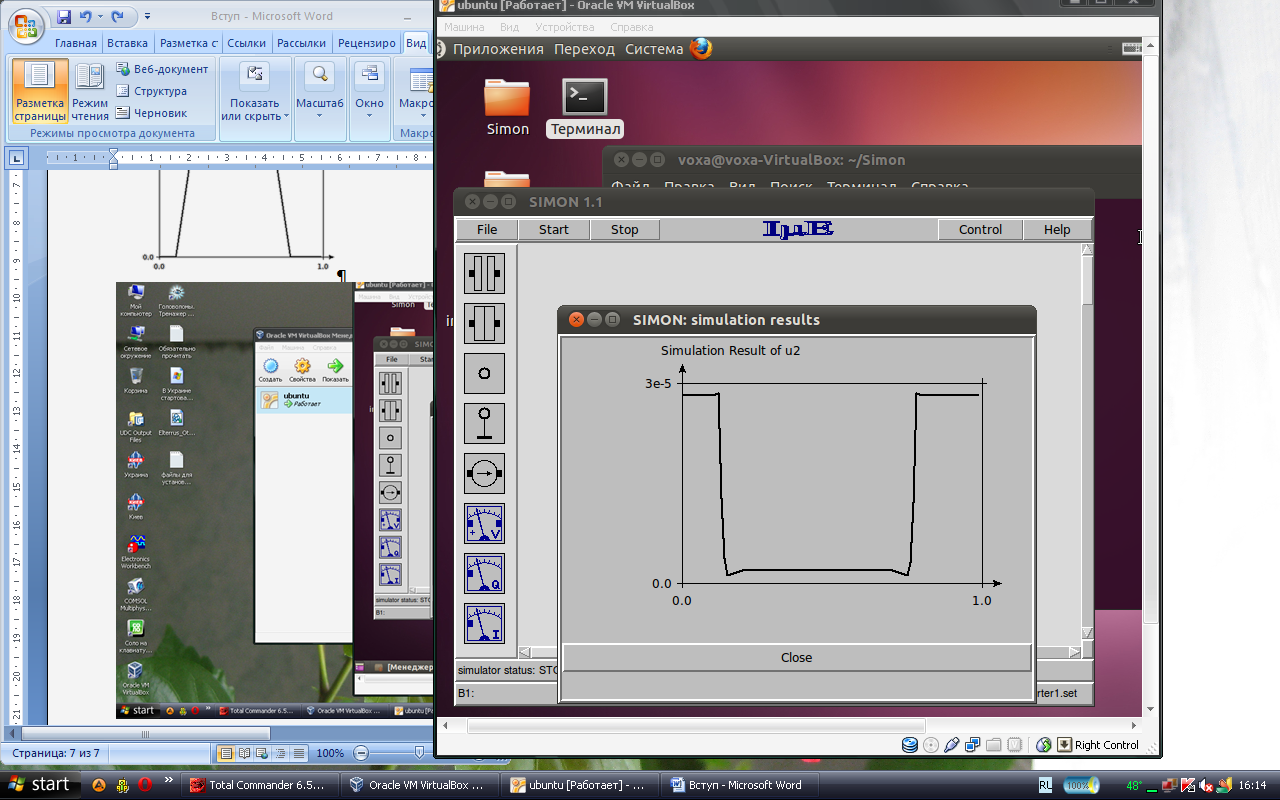
де С∑=С1+С2+Сg визначає повну ємність острівця. Якщо розглянути залежність кулонівської блокади від величини початкового заряду, то вона зменшується і зникає повністю при Qb=0.5q (рис.6. 3, Система SIMON не має жодних початкових обмежень, таких як кількість острівців, тунельних переходів або обов’язкове заземлення джерел напруги. Він може працювати з джерелами сталої, лінійно залежної від часу, кусково – лінійної та напруги, залежної від напруги. Особливістю системи є графічний інтерфейс користувача та графічний редактор виконані на tcl/tk. Графічний редактор схем підтримує drag-and-drop для моделювання одноелектронних схем. Параметри можуть бути зміненими інтерактивно, а результати моделювання можуть бути наведені в графічній формі. Звичайно ж, всі параметри моделювання, такі як режим моделювання, порядок тунелювання і температура середовища можуть бути змінені. На рис. В.4 показані приклади скріншотів системи SIMON.
Рис. 6.4. Скріншоти системи моделювання SIMON
|
|||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 413; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

 , яка потрібна при зарядженні квантового острівця одним електроном:
, яка потрібна при зарядженні квантового острівця одним електроном: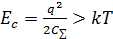 , (6.1)
, (6.1) — це повна ємність острівця. Якщо ця кулонівська енергія перевищує вільну термодинамічну, то рух електронів стає контрольованим та залежним від джерел живлення.
— це повна ємність острівця. Якщо ця кулонівська енергія перевищує вільну термодинамічну, то рух електронів стає контрольованим та залежним від джерел живлення. (6.2)
(6.2) , (6.3)
, (6.3) – це матриця ємностей, V,
– це матриця ємностей, V,  і
і  ,
, 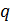 — відомі та невідомі частини вузлових напруг і зарядів.
— відомі та невідомі частини вузлових напруг і зарядів. . (6.4)
. (6.4) , (6.5)
, (6.5)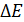 — це зміна вільної енергії Гельмогольця, RT — опір тунельного переходу і
— це зміна вільної енергії Гельмогольця, RT — опір тунельного переходу і  — термодинамічна енергія. Вільна енергія Гельмольця визначається різницею між електростатичною енергією, яка накопичена в колі, та роботою, виконаною джерелами напруги:
— термодинамічна енергія. Вільна енергія Гельмольця визначається різницею між електростатичною енергією, яка накопичена в колі, та роботою, виконаною джерелами напруги: (6.6)
(6.6) , (6.7)
, (6.7) —електростатична енергія,
—електростатична енергія,  — робота, виконана джерелами напруги,
— робота, виконана джерелами напруги, 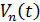 — напруга n-го джерела напруги і
— напруга n-го джерела напруги і  — струми, які протікають через відповідні джерела напруги.
— струми, які протікають через відповідні джерела напруги. (6.8)
(6.8)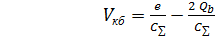 для
для  =[0, 0.25 q, 0.5q], (6.9)
=[0, 0.25 q, 0.5q], (6.9) ), Отже, початково немає інформації про фоновий заряд. В гіршому випадку кулонівська блокада зникає зовсім і поведінка транзистора повністю змінюється.
), Отже, початково немає інформації про фоновий заряд. В гіршому випадку кулонівська блокада зникає зовсім і поведінка транзистора повністю змінюється.