
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Електростатичні моделі квантових автоматів
Будемо моделювати комірку, показану на рис. 2.1, використовуючи гамільтоніан типу Хаббарда. Для ізольованої комірки гамільтоніан може бути записаний у вигляді:
де Для електростатичної моделі квантової комірки отримаємо значення параметрів у гамільтоніані із простої, експериментально прийнятної моделі. Зазвичай, діаметр квантової точки не перевищує 10 нм, і беремо Це корисно для визначення кількості, яка відображає ступінь до якої щільність заряду для даного власного стану системи вирівнюється лінійно. Таке вирівнювання може бути або вздовж лінії, що проходить через положення 1 і 3 або вздовж лінії, що проходить через положення 2 і 4 (рис.4.1). Для кожного положення, обчислюємо одиничну часткову щільність
Для ізольованої комірки з усіма місцевими енергіями, відсутність поляризація є найстабільнішою. Нижче побачимо, що збудження через вплив збудження в сусідніх комірках може призвести до сильної поляризованості початкового стану. Поляризацію, визначену таким чином, не слід плутати із звичайною дипольною поляризацією суцільного однорідного середовища. Вона просто відображає ступінь, до якої електрони в комірці вирівнюються і в якому з двох можливих напрямків вирівнювання відбувається. Звернемо увагу на те, що у комірці не існує впливу дипольного моменту. Взаємодія комірки з навколишнім однорідним середовищем, у тому числі іншими сусідніми комірками, міститься у другому члені гамільтоніану(4.1), який записується у формі
Спіни двох електронів можуть бути однонаправленими або анти-однонаправленими, з відповідними змінами в просторовій частині хвильової функції за принципом Паулі. Обмежимо наш аналіз на випадок анти-однонаправлених спінів тому, що це основні конфігурації; випадок спінів однонаправлених описується майже ідентично. Гамільтоніан діагоналізуется безпосередньо в основі декількох електронних станів. Розрахуємо одночасткові густини заряду,
і з урахуванням щільності (4.2), отримаємо результуючу поляризацію
|
|||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.107.161 (0.032 с.) |

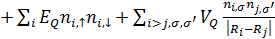 , (4.1)
, (4.1) є оператором анігіляції, що руйнує частки в положенні
є оператором анігіляції, що руйнує частки в положенні  зі спіном
зі спіном  . Номер оператора для положення
. Номер оператора для положення 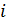 і спін
і спін  . Електростатична енергія для
. Електростатична енергія для  ; енергія зв'язку з центральною точкою є
; енергія зв'язку з центральною точкою є 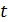 ; енергія заряду для однієї точкою є
; енергія заряду для однієї точкою є  . Останній параметр відображає кулонівський потенціал енергії для двох електронів, що знаходяться в положеннях
. Останній параметр відображає кулонівський потенціал енергії для двох електронів, що знаходяться в положеннях  на позиції
на позиції  і
і  . Якщо не вказано інше, будемо розглядати випадок, коли існує електростатична рівновага
. Якщо не вказано інше, будемо розглядати випадок, коли існує електростатична рівновага  .
. . Відстань тунелювання між центрами точок вважається рівною 20 нм. Сила кулонівського зв'язку,
. Відстань тунелювання між центрами точок вважається рівною 20 нм. Сила кулонівського зв'язку,  , розраховується для матеріалу з діелектричною проникністю 10. Припускаємо, що
, розраховується для матеріалу з діелектричною проникністю 10. Припускаємо, що  і
і 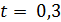 меВ.
меВ. , яка є просто середнє значення повного оператора власного стану двох електронів. Поляризація комірки,
, яка є просто середнє значення повного оператора власного стану двох електронів. Поляризація комірки, 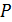 , визначається як:
, визначається як: . (4.2)
. (4.2) . Розв’яжемо статичне рівняння Шредінгера для стану комірки
. Розв’яжемо статичне рівняння Шредінгера для стану комірки  під впливом сусідніх комірок:
під впливом сусідніх комірок: . (4.3)
. (4.3) ,
, (4.4)
(4.4) , дорівнює
, дорівнює  . Для ізольованої комірки, це не має ніякого ефекту і включає місцеву енергію. Протягом кількох комірок у безпосередній близькості, як буде розглянуто нижче, підтримка загальної нейтральності комірки означає, що міжкоміркову взаємодію обумовлює диполь, квадрупольного та вищих моментів розподілу заряду комірки. Якщо комірка мала чистий сумарний заряд електронів, то в комірках на периферії групи комірок будуть мати тенденцію реагувати на основний сумарний заряд перемикання оточуючих КА.
. Для ізольованої комірки, це не має ніякого ефекту і включає місцеву енергію. Протягом кількох комірок у безпосередній близькості, як буде розглянуто нижче, підтримка загальної нейтральності комірки означає, що міжкоміркову взаємодію обумовлює диполь, квадрупольного та вищих моментів розподілу заряду комірки. Якщо комірка мала чистий сумарний заряд електронів, то в комірках на периферії групи комірок будуть мати тенденцію реагувати на основний сумарний заряд перемикання оточуючих КА.


