Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о рядах в комплексной области.Содержание книги
Поиск на нашем сайте
Если членами ряда являются комплексные числа, то ряд примет вид: Определение: Ряд (1) называется сходящимся если сходится по отдельности ряд, составленный из действительных частей данного ряда: Пусть Тогда суммой ряда (1) называется число Теорема 17. Если сходится ряд модулей членов ряда (1) то ряд(1) так же сходится. Доказательство.
Степенным рядом в комплексной области называется ряд: где
По теореме 17(4) сходится если сходится ряд:
Пример. Вычислить интеграл Решение. б). Путь интегрирования l - ломаная ОВА, О (0,0), В (1,0), А (1,1). Для отрезка ОВ имеем: y = 0, Заметим, что подинтегральная функция в данном примере - функция не аналитическая, поэтому интегралы по двум различным кривым, соединяющим две данные точки, могут иметь различные значения, что и продемонстрировано в этом примере. Пример. Вычислить интеграл от аналитической функции
Применяем формулу (3), первообразную находим, используя методы интегрирования действительного анализа: Пример. Разложить функцию Решение. Так как функция является рациональной дробью, то особыми точками являются нули знаменателя, т.е. z 1 = -1 и z 2 = 3. Запишем функцию в виде Кольца аналитичности | z | < 1, 1 < | z | < 3, | z | > 3. Раскладываем дробь на элементарные дроби: При | z | < 1 имеем: Таким образом, в круге | z | < 1 функция раскладывается в ряд Тейлора: В кольце 1 < | z | < 3: В итоге имеем: В круге | z | > 3: В итоге имеем: Пример. Разложить функцию f (z) = z 3· e 1/ z в окрестности точки z 0 = 0. Решение. Из основного разложения
или Литература Основная 1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах [Текст]: [учеб. Пособие для втузов]: В 2-х ч. Ч.1.-6-е изд. - М.: ОНИКС 21 век, 2012 (30714). – 304 с.: ил. – 119-00. 2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах [Текст]: [учеб. Пособие для втузов]: В 2-х ч. Ч.2.-6-е изд. - М.: ОНИКС 21 век, 2012 (20914).– 416 с.: ил. – Библиогр.: с.416 (10 назв.). – 119-00. 3. Бугров Я.С., Никольский С.М. Высшая математика: В 3-х т.; Учеб. для вузов инж.-техн. спец. Т. 3: Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного.; [Под ред. Садовничего В.А.]. ‑ 6-е изд., стер. ‑ М.: Дрофа, 2011 (80514). ‑ 511 с. – (Высшее образование: Современный учебник). – 117-00.
Дополнительная 1. Пантина И.В. Вычислительная математика [Электронный ресурс]: учебник/- М.: МФПУ Синергия, 2012.-176 с.- http://znanium.com/. 2. Гмурман В.Е. Ттеория вероятностей и математическая статистика: Учеб. Пособие для вузов / В.Е. Гмурман. – 10-е изд., стер. - М.: Высш.шк., 2011 (90514). – 404 с. – 175-00.
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.68.228 (0.007 с.) |

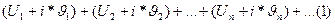 где
где 
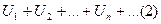 и ряд составленный из мнимых частей:
и ряд составленный из мнимых частей:  .
.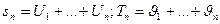 то ряд (1) сходится
то ряд (1) сходится 
 .
. - сходится.
- сходится. (2) сходится по признаку сравнения.
(2) сходится по признаку сравнения. (3) сходится по признаку сравнения при чем абсолютно по определению (1) сходимости.
(3) сходится по признаку сравнения при чем абсолютно по определению (1) сходимости.
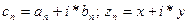 (4)
(4) где
где 
 - действительные числа=> можно применять все известные признаки.
- действительные числа=> можно применять все известные признаки.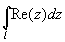 , где:
, где: 
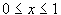 .
. 

 .
. 
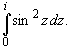

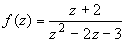 в ряд Лорана по степеням z.
в ряд Лорана по степеням z.



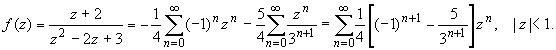



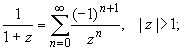


 получаем
получаем