
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительные интервалы. Доверительная вероятностьСодержание книги
Поиск на нашем сайте
Интервальной называют оценку неизвестного параметра, которая определяется двумя числами – концами интервалов. Доверительной вероятностью называется вероятность того, что точечная оценка параметра отклонится по модулю от оцениваемого параметра не более, чем на заданное значение δ:
Значение γ называют надежностью оценки. Неравенство
Задача 1. Дано: Х – количественный признак, распределенный нормально;
Найти: доверительный интервал для М(Х)=а. Будем рассматривать выборочную среднюю
Тогда (по доказанному выше) М( P P
Итак, доверительный интервал для математического ожидания нормально распределенной случайной величины Х в случае известного среднего квадратического отклонения:
δ – среднее квадратическое отклонение; n – объем выборки;
t – аргумент интегральной функции Лапласа, такой, что
Задача 2. Дано: Х - распределено нормально;
Найти: доверительный интервал для М(Х)=а Случайная величина
n – объем выборки.
Параметр Итак, доверительный интервал для математического ожидания нормально распределенной случайной величины Х в случае неизвестной дисперсии:
Задача 3. Оценить вероятность появления события А по относительной частоте. Пусть произведено Точечные оценки математического ожидания и дисперсии для случайной величины
Если n достаточно велико, то
Если w>p, то Возведем в квадрат обе части неравенства, преобразуем выражение, получим квадратное неравенство относительно неизвестной вероятности Тогда
Доверительный интервал для вероятности:
Замечание. Если известно распределение Х, но неизвестны его параметры, то для их определения используют метод моментов Пирсона. Приравнивают теоретические моменты к соответствующим эмпирическим моментам, и находят из полученной системы уравнений неизвестные параметры.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.130.174 (0.007 с.) |

 .
.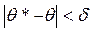 задает доверительный интервал:
задает доверительный интервал:
 - интервальная оценка параметра θ или доверительный интервал, в который с вероятностью γ попадает истинное значение оцениваемого параметра.
- интервальная оценка параметра θ или доверительный интервал, в который с вероятностью γ попадает истинное значение оцениваемого параметра. – среднее квадратическое отклонение.
– среднее квадратическое отклонение. как случайную величину (так как она меняется от выборки к выборке);
как случайную величину (так как она меняется от выборки к выборке);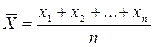
 - распр. нормально, с
- распр. нормально, с  и
и 
 )=а,
)=а, 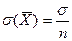


 найдем по таблице функции Лапласа:
найдем по таблице функции Лапласа:  =>
=> 
 ,
, - надежность;
- надежность; .
. - неизвестно.
- неизвестно. имеет распределение Стьюдента с k=n-1 степенями свободы;
имеет распределение Стьюдента с k=n-1 степенями свободы; - выборочная средняя;
- выборочная средняя; – «исправленное» среднее квадратическое отклонение,
– «исправленное» среднее квадратическое отклонение, - плотность распределение Стьюдента, определяется параметром n (не зависит от а и σ).
- плотность распределение Стьюдента, определяется параметром n (не зависит от а и σ). =
= 
 можно найти по таблице распределения Стьюдента для заданных n и γ.
можно найти по таблице распределения Стьюдента для заданных n и γ. ,
, независимых испытаний с неизвестной вероятностью появления события А в каждом испытании.
независимых испытаний с неизвестной вероятностью появления события А в каждом испытании.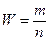 соответственно равны:
соответственно равны: и
и  .
.
 ;
; => t по таблице функции Лапласа:
=> t по таблице функции Лапласа: 

 .
. , где корни квадратного трехчлена
, где корни квадратного трехчлена



