Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Специальные главы математикмиСтр 1 из 9Следующая ⇒
СПЕЦИАЛЬНЫЕ ГЛАВЫ МАТЕМАТИКМИ Курс лекций Для направления 16.04.03 Холодильная, криогенная техника и системы жизнеобеспечения СОСТАВИТЕЛИ: К.т.н., доц. Наумова Н.А. К.т.н.,доц. Данович Л.М. Г. СОДЕРЖАНИЕ
§ 1. Основные понятия и определения.
Современная статистика разрабатывает планирование эксперимента, занимается последующим анализом и др. Если требуется изучить совокупность однородных объектов относительно некоторого признака, то на практике не изучают каждый элемент, а случайно отбирают ограниченное число объектов и изучают их. Выборкой называют совокупность случайно отобранных объектов. Генеральной называется совокупность объектов, из которых производится выборка. Объем совокупности – это число объектов этой совокупности.
Наиболее удобно выборку записывать в виде таблицы:
где наблюдаемые значения хi называются вариантами (каждое из хi наблюдалось ni раз), а указанная последовательность вариант, записанных в возрастающем порядке называется вариационным рядом, ni – частоты. Сравнение двух средних генеральных совокупностей Решение. Критерий
Пример 2. Фирма предлагает автоматы по разливу напитков. При выборе n=16 найдено Решение.
Элементы теории корреляции Пусть X и Y – случайные величины Они могут быть: 1) независимы; 2) связаны строгой функциональной зависимостью (встречается редко в силу воздействия случайных факторов); 3) связаны статистической зависимостью (при которой изменение одной из величин влечет изменение распределения другой величины). В частности, корреляционной называется зависимость, при которой изменение одной величины влечет изменение среднего значения другой.
Его график – выборочная линия регрессии Y на X. Выборочный коэффициент корреляции:
где
1) 2) Выборочное уравнение прямой линии регрессии
Замечание: при вычислении удобно использовать условные варианты:
Коэффициент Пример.
1) 2) 3) 4) Решив систему линейных уравнений (1-4), получим значения неизвестных параметров
Дискриминантный анализ Дискриминантный анализ используется для принятия решения о том, какие переменные различают (дискриминируют) две или более возникающие совокупности (группы). Например, некий исследователь в области образования может захотеть исследовать, какие переменные относят выпускника средней школы к одной из трех категорий: (1) поступающий в колледж, (2) поступающий в профессиональную школу или (3) отказывающийся от дальнейшего образования или профессиональной подготовки. Для этой цели исследователь может собрать данные о различных переменных, связанных с учащимися школы. После выпуска большинство учащихся естественно должно попасть в одну из названных категорий. Затем можно использовать Дискриминантный анализ для определения того, какие переменные дают наилучшее предсказание выбора учащимися дальнейшего пути. Пошаговый дискриминантный анализ: Вероятно, наиболее общим применением дискриминантного анализа является включение в исследование многих переменных с целью определения тех из них, которые наилучшим образом разделяют совокупности между собой. Модель. Другими словами, вы хотите построить "модель", позволяющую лучше всего предсказать, к какой совокупности будет принадлежать тот или иной образец. В следующем рассуждении термин "в модели" будет использоваться для того, чтобы обозначать переменные, используемые в предсказании принадлежности к совокупности; о неиспользуемых для этого переменных будем говорить, что они "вне модели". Пошаговый анализ с включением. В пошаговом анализе дискриминантных функций модель дискриминации строится по шагам. Точнее, на каждом шаге просматриваются все переменные и находится та из них, которая вносит наибольший вклад в различие между совокупностями. Эта переменная должна быть включена в модель на данном шаге, и происходит переход к следующему шагу. Пошаговый анализ с исключением. Можно также двигаться в обратном направлении, в этом случае все переменные будут сначала включены в модель, а затем на каждом шаге будут устраняться переменные, вносящие малый вклад в предсказания. Тогда в качестве результата успешного анализа можно сохранить только "важные" переменные в модели, то есть те переменные, чей вклад в дискриминацию больше остальных. F для включения, F для исключения. Эта пошаговая процедура "руководствуется" соответствующим значением F для включения и соответствующим значением F для исключения. Значение F статистики для переменной указывает на ее статистическую значимость при дискриминации между совокупностями, то есть, она является мерой вклада переменной в предсказание членства в совокупности. Если вы знакомы с пошаговой процедурой множественной регрессии, то вы можете интерпретировать значение F для включения/исключения в том же самом смысле, что и в пошаговой регрессии. Расчет на случай. Пошаговый дискриминантный анализ основан на использовании статистического уровня значимости. Поэтому по своей природе пошаговые процедуры рассчитывают на случай, так как они "тщательно перебирают" переменные, которые должны быть включены в модель для получения максимальной дискриминации. При использовании пошагового метода исследователь должен осознавать, что используемый при этом уровень значимости не отражает истинного значения альфа, то есть, вероятности ошибочного отклонения гипотезы H0 (нулевой гипотезы, заключающейся в том, что между совокупностями нет различия).
Интерпретация функции дискриминации для двух групп: Для двух групп дискриминантный анализ может рассматриваться также как процедура множественной регрессии (и аналогичная ей) - (см. раздел Множественная регрессия; дискриминантный анализ для двух групп также называется Линейным дискриминантным анализом Фишера после работы Фишера (Fisher, 1936). (С вычислительной точки зрения все эти подходы аналогичны). Если вы кодируете две группы как 1 и 2, и затем используете эти переменные в качестве зависимых переменных в множественной регрессии, то получите результаты, аналогичные тем, которые получили бы с помощью Дискриминантного анализ а. В общем, в случае двух совокупностей вы подгоняете линейное уравнение следующего типа: Группа = a + b1*x1 + b2*x2 +... + bm*xm где a является константой, и b1... bm являются коэффициентами регрессии. Интерпретация результатов задачи с двумя совокупностями тесно следует логике применения множественной регрессии: переменные с наибольшими регрессионными коэффициентами вносят наибольший вклад в дискриминацию. Дискриминантные функции для нескольких групп: Если имеется более двух групп, то можно оценить более, чем одну дискриминантную функцию подобно тому, как это было сделано ранее. Например, когда имеются три совокупности, вы можете оценить: (1) - функцию для дискриминации между совокупностью 1 и совокупностями 2 и 3, взятыми вместе, и (2) - другую функцию для дискриминации между совокупностью 2 и совокупности 3. Например, вы можете иметь одну функцию, дискриминирующую между теми выпускниками средней школы, которые идут в колледж, против тех, кто этого не делает (но хочет получить работу или пойти в училище), и вторую функцию для дискриминации между теми выпускниками, которые хотят получить работу против тех, кто хочет пойти в училище. Коэффициенты b в этих дискриминирующих функциях могут быть проинтерпретированы тем же способом, что и ранее. Методы кластерного анализа
Основные понятия теории поля. Скалярное поле. Векторное поле. Оператор Гамильтона Векторным полем называется область, каждой точке которой поставлен в соответствие вектор Производная по направлению. Пусть z=f(x;y) – определена в некоторой окрестности точки P(x;y). Пусть
U
Определение: Предел отношения приращения функции в направлении Введем формулу для
(1) =>
=> Производная по направлению есть скорость изменения функции z=f(x;y) в данном направлении. Замечание: Частные производные можно рассматривать как производные по направлению
Градиент. Пусть z=f(x;y) определена и непрерывна вместе с частными производными в некоторой окрестности точки P0(x0;y0). Определение: Вектор координатами, которого являются частные производные в точке: Gradz(x0;y0)= ТЕОРЕМА: Скалярное произведение градиента в точке P на направление
Доказательство: gradz Следствие: Это выражение принимает наибольшее значение при Т.е. когда Т.е. направление градиента есть направление максимального роста функции. Замечание: Для функции трех переменных: Gradu={ux’; uy’; uz’}∙ Комплексные числа Выражение вида z=x+yi=ρ(cosφ + i sinφ) называется комплексным числом (в алгебраической и тригонометрической форме соответственно). Здесь i2 = -1, x = Re(z) — действительная часть, a y=Im(z) — мнимая часть комплексного числа z, р и φ — соответственно, модуль и аргумент числа z:
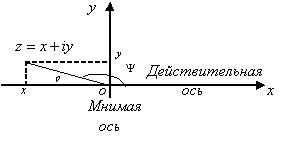
Комплексные числа изображаются точками (рис.4) на комплексной плоскости.
Рисунок 4 – изображение комплексного числа Извлечение корня п – й степени (п – натуральное число) из числа z = ρ(cosφ + i sinφ) (z
где Пример. Изобразить на комплексной плоскости числа Решение. 1) Для числах z1 имеем x1 = Re z1 = -8, y1 = Im z1 = 0. Откладывая по оси Ox х1 = -8, а по оси Оу у1 = 0, получаем точку комплексной плоскости, соответствующую числу z1 (рис. 8). Модуль этого числа находим по формуле (7): 2) Модуль числа z2 равен
Рисунок 8 – графическое изображение числа z2
Пример. Вычислить Решение. Модуль числа -8 равен 8, а аргумент равен
Пример. Вычислить интеграл от аналитической функции
Применяем формулу (3), первообразную находим, используя методы интегрирования действительного анализа: Пример. Разложить функцию Решение. Так как функция является рациональной дробью, то особыми точками являются нули знаменателя, т.е. z 1 = -1 и z 2 = 3. Запишем функцию в виде Кольца аналитичности | z | < 1, 1 < | z | < 3, | z | > 3. Раскладываем дробь на элементарные дроби: При | z | < 1 имеем: Таким образом, в круге | z | < 1 функция раскладывается в ряд Тейлора: В кольце 1 < | z | < 3: В итоге имеем: В круге | z | > 3: В итоге имеем: Пример. Разложить функцию f (z) = z 3· e 1/ z в окрестности точки z 0 = 0. Решение. Из основного разложения
или Литература Основная 1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах [Текст]: [учеб. Пособие для втузов]: В 2-х ч. Ч.1.-6-е изд. - М.: ОНИКС 21 век, 2012 (30714). – 304 с.: ил. – 119-00. 2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах [Текст]: [учеб. Пособие для втузов]: В 2-х ч. Ч.2.-6-е изд. - М.: ОНИКС 21 век, 2012 (20914).– 416 с.: ил. – Библиогр.: с.416 (10 назв.). – 119-00. 3. Бугров Я.С., Никольский С.М. Высшая математика: В 3-х т.; Учеб. для вузов инж.-техн. спец. Т. 3: Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного.; [Под ред. Садовничего В.А.]. ‑ 6-е изд., стер. ‑ М.: Дрофа, 2011 (80514). ‑ 511 с. – (Высшее образование: Современный учебник). – 117-00.
Дополнительная 1. Пантина И.В. Вычислительная математика [Электронный ресурс]: учебник/- М.: МФПУ Синергия, 2012.-176 с.- http://znanium.com/. 2. Гмурман В.Е. Ттеория вероятностей и математическая статистика: Учеб. Пособие для вузов / В.Е. Гмурман. – 10-е изд., стер. - М.: Высш.шк., 2011 (90514). – 404 с. – 175-00.
СПЕЦИАЛЬНЫЕ ГЛАВЫ МАТЕМАТИКМИ Курс лекций
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.118.95 (0.098 с.) |
 - случайная величина, имеющая распределение Стьюдента.
- случайная величина, имеющая распределение Стьюдента. :
: 
 :
: 
 <2900
<2900
 - левосторонняя критическая точка
- левосторонняя критическая точка =>
=> 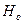 отвергается
отвергается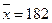 г дозы в стакане автоматом №1. По выборке m=9 найдена
г дозы в стакане автоматом №1. По выборке m=9 найдена  г дозы, наливаемой в стакан автоматом №2. По утверждению изготовить сл/в наливаемой дозы имеет нормальный знач распределения с
г дозы, наливаемой в стакан автоматом №2. По утверждению изготовить сл/в наливаемой дозы имеет нормальный знач распределения с 
 . Можно ли считать, что автомат №2 наливает в стакан большую дозу напитка.
. Можно ли считать, что автомат №2 наливает в стакан большую дозу напитка. ;
;  ;
;  ;
; 
 ;
; 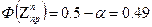
 =>
=> 
 => принимается
=> принимается  - выборочное уравнение регрессии.
- выборочное уравнение регрессии. ,
, - варианты;
- варианты;  - частота пары вариант
- частота пары вариант  ;
;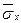 ,
,  - выборочные средние квадратические отклонения;
- выборочные средние квадратические отклонения;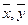 - выборочные средние.
- выборочные средние.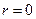 - X и Y – независимы;
- X и Y – независимы; - X и Y связаны линейной функциональной зависимостью
- X и Y связаны линейной функциональной зависимостью 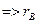 измеряет силу линейной связи между X и Y.
измеряет силу линейной связи между X и Y.
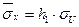 ;
; 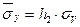 ;
; 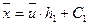 ;
; 
 - выборочный коэффициент регрессии Y на X.
- выборочный коэффициент регрессии Y на X.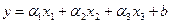



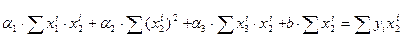

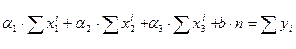
 . Найти ее решение можно, например, по формулам Крамера.
. Найти ее решение можно, например, по формулам Крамера. В модуле Кластерный анализ реализован полный набор методов кластерного анализа данных, включая методы k-средних, иерархической кластеризации и двухвходового объединения. Данные могут поступать как в исходном виде, так и в виде матрицы расстояний между объектами. Наблюдения, переменные или и наблюдения, и переменные можно кластеризовать, используя различные меры расстояния (евклидово, квадрат евклидова, городских кварталов (манхэттеновское), Чебышева, степенное, процент несогласия и 1- коэффициент корреляции Пирсона) и различные правила объединения (связывания) кластеров (одиночная, полная связь, невзвешенное и взвешенное попарное среднее по группам, невзвешенное, взвешенное расстояние между центрами, метод Варда и другие). Матрицы расстояний можно сохранять для дальнейшего анализа в других модулях системы STATISTICA. При проведении кластерного анализа методом k-средних пользователь имеет полный контроль над начальным расположением центров кластеров. Могут быть выполнены чрезвычайно большие планы анализа: так например, при иерархическом (древовидном) связывании можно работать с матрицей из 90 тыс. расстояний. Помимо стандартных результатов кластерного анализа, в модуле доступен также разнообразный набор описательных статистик и расширенных диагностических методов (полная схема объединения с пороговыми уровнями при иерархической кластеризации, таблица дисперсионного анализа при кластеризации методом k-средних). Информация о принадлежности объектов к кластерам может быть добавлена к файлу данных и использоваться в дальнейшем анализе. Графические возможности модуля Кластерный анализ включают настраиваемые дендрограммы, двухвходовые диаграммы объединений, графическое представление схемы объединения, диаграмму средних при кластеризации по методу k-средних и многое другое.
В модуле Кластерный анализ реализован полный набор методов кластерного анализа данных, включая методы k-средних, иерархической кластеризации и двухвходового объединения. Данные могут поступать как в исходном виде, так и в виде матрицы расстояний между объектами. Наблюдения, переменные или и наблюдения, и переменные можно кластеризовать, используя различные меры расстояния (евклидово, квадрат евклидова, городских кварталов (манхэттеновское), Чебышева, степенное, процент несогласия и 1- коэффициент корреляции Пирсона) и различные правила объединения (связывания) кластеров (одиночная, полная связь, невзвешенное и взвешенное попарное среднее по группам, невзвешенное, взвешенное расстояние между центрами, метод Варда и другие). Матрицы расстояний можно сохранять для дальнейшего анализа в других модулях системы STATISTICA. При проведении кластерного анализа методом k-средних пользователь имеет полный контроль над начальным расположением центров кластеров. Могут быть выполнены чрезвычайно большие планы анализа: так например, при иерархическом (древовидном) связывании можно работать с матрицей из 90 тыс. расстояний. Помимо стандартных результатов кластерного анализа, в модуле доступен также разнообразный набор описательных статистик и расширенных диагностических методов (полная схема объединения с пороговыми уровнями при иерархической кластеризации, таблица дисперсионного анализа при кластеризации методом k-средних). Информация о принадлежности объектов к кластерам может быть добавлена к файлу данных и использоваться в дальнейшем анализе. Графические возможности модуля Кластерный анализ включают настраиваемые дендрограммы, двухвходовые диаграммы объединений, графическое представление схемы объединения, диаграмму средних при кластеризации по методу k-средних и многое другое. , проекции которого на координатные оси являются функциями координат точки M(x,y). P = P(x,y), Q = Q(x,y), то есть
, проекции которого на координатные оси являются функциями координат точки M(x,y). P = P(x,y), Q = Q(x,y), то есть  -вектор-функция. /Аналогично в пространстве/.
-вектор-функция. /Аналогично в пространстве/. задает некоторое направление;
задает некоторое направление;  получаем из P(x;y) при перемещении в направлении
получаем из P(x;y) при перемещении в направлении 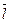 .
. f
f  - f(x;y) – приращение функции в направлении
- f(x;y) – приращение функции в направлении  l – длина отрезка PP1, величина перемещения
l – длина отрезка PP1, величина перемещения
 l
l  (1)
(1) (2)
(2) при условии, что z=f(x;y)
при условии, что z=f(x;y)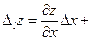



 (3)
(3) и
и 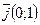 .
.
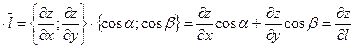

 =0
=0
 .
. (7)
(7)
 0) производится по формуле
0) производится по формуле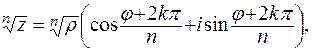 (8)
(8) — арифметический корень из модуля z, a k = 0,1, …, n – 1.
— арифметический корень из модуля z, a k = 0,1, …, n – 1. ,
, 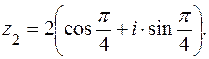 Записать число z1 в тригонометрической, а число z2 — в алгебраической форме.
Записать число z1 в тригонометрической, а число z2 — в алгебраической форме. . Аргумент определяемиз равенства
. Аргумент определяемиз равенства  . Taккак число z1 находится в левой полуплоскости, то его аргумент
. Taккак число z1 находится в левой полуплоскости, то его аргумент  . Тригонометрическая форма числа z1 имеет вид
. Тригонометрическая форма числа z1 имеет вид 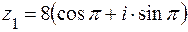 .
. , а аргумент
, а аргумент  . Для его изображения на комплексной плоскости проводимиз полюса луч под углом
. Для его изображения на комплексной плоскости проводимиз полюса луч под углом  к полярной оси и откладываем на нем отрезок длиной р2 = 2. Полученная точка соответствует числу z2 (рис. 8). Егодействительнаячасть
к полярной оси и откладываем на нем отрезок длиной р2 = 2. Полученная точка соответствует числу z2 (рис. 8). Егодействительнаячасть 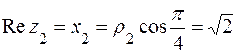 , а мнимая часть
, а мнимая часть 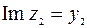 ,
, 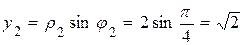 . Таким образом, алгебраическая формачисла z2 имеетвид
. Таким образом, алгебраическая формачисла z2 имеетвид  .
.
 .
. . Используя формулу (8), получаем
. Используя формулу (8), получаем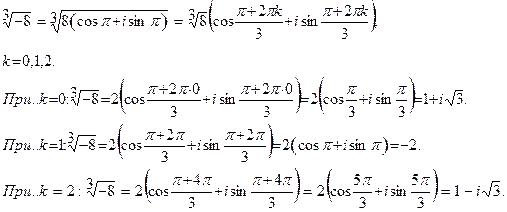
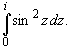

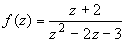 в ряд Лорана по степеням z.
в ряд Лорана по степеням z.



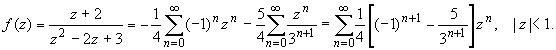



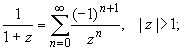


 получаем
получаем