
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Факторный анализ и анализ главных компонентСодержание книги
Поиск на нашем сайте
Векторный анализ и теория поля Основные понятия теории поля. Скалярное поле. Векторное поле. Оператор Гамильтона Векторным полем называется область, каждой точке которой поставлен в соответствие вектор Производная по направлению. Пусть z=f(x;y) – определена в некоторой окрестности точки P(x;y). Пусть
U
Определение: Предел отношения приращения функции в направлении Введем формулу для
(1) =>
=> Производная по направлению есть скорость изменения функции z=f(x;y) в данном направлении. Замечание: Частные производные можно рассматривать как производные по направлению
Градиент. Пусть z=f(x;y) определена и непрерывна вместе с частными производными в некоторой окрестности точки P0(x0;y0). Определение: Вектор координатами, которого являются частные производные в точке: Gradz(x0;y0)= ТЕОРЕМА: Скалярное произведение градиента в точке P на направление Доказательство: gradz Следствие: Это выражение принимает наибольшее значение при Т.е. когда Т.е. направление градиента есть направление максимального роста функции. Замечание: Для функции трех переменных: Gradu={ux’; uy’; uz’}∙
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 Модуль Факторный анализ содержит широкий набор статистик и методов факторного анализа (и иерархического факторного анализа) с расширенной диагностикой и большим многообразием исследовательских и разведочных графиков. Здесь можно выполнять анализ (общий и иерархический косоугольный) главных компонент и главных факторов для наборов данных, содержащих до 300 переменных (модели большего объема можно исследовать средствами модуля Моделирование структурными уравнениями). Выходные результаты включают: собственные значения (обычные, кумулятивные и относительные), нагрузки факторов и коэффициенты факторных баллов (которые можно добавить к файлу входных данных, просмотреть на пиктографике и в интерактивном режиме перекодировать), а также некоторые боле специальные статистики и диагностики. В распоряжении пользователя имеются следующие методы вращения факторов: варимакс, биквартимакс, квартимакс и эквимакс (по нормализованным либо первоначальным нагрузкам), а также косоугольные вращения. Пространство факторов можно визуально просматривать "срез за срезом" на двух- или трехмерных диаграммах рассеяния с отмеченными точками данных; среди других графических средств - графики "каменистой осыпи", различные типы диаграмм рассеяния, гистограммы, линейные графики и др. После того, как факторное решение определено, пользователь может вычислить (воспроизвести) корреляционную матрицу и оценить согласованность факторной модели путем анализа остаточной корреляционной матрицы (или остаточной дисперсионной/ковариационной матрицы). На входе можно использовать как исходные данные, так и матрицы корреляций. Подтверждающий факторный анализ и другие связанные с ним виды анализа могут быть выполнены средствами модуля Моделирование структурными уравнениями, где специальный Мастер подтверждающего факторного анализа проведет пользователя через все этапы построения модели.
Модуль Факторный анализ содержит широкий набор статистик и методов факторного анализа (и иерархического факторного анализа) с расширенной диагностикой и большим многообразием исследовательских и разведочных графиков. Здесь можно выполнять анализ (общий и иерархический косоугольный) главных компонент и главных факторов для наборов данных, содержащих до 300 переменных (модели большего объема можно исследовать средствами модуля Моделирование структурными уравнениями). Выходные результаты включают: собственные значения (обычные, кумулятивные и относительные), нагрузки факторов и коэффициенты факторных баллов (которые можно добавить к файлу входных данных, просмотреть на пиктографике и в интерактивном режиме перекодировать), а также некоторые боле специальные статистики и диагностики. В распоряжении пользователя имеются следующие методы вращения факторов: варимакс, биквартимакс, квартимакс и эквимакс (по нормализованным либо первоначальным нагрузкам), а также косоугольные вращения. Пространство факторов можно визуально просматривать "срез за срезом" на двух- или трехмерных диаграммах рассеяния с отмеченными точками данных; среди других графических средств - графики "каменистой осыпи", различные типы диаграмм рассеяния, гистограммы, линейные графики и др. После того, как факторное решение определено, пользователь может вычислить (воспроизвести) корреляционную матрицу и оценить согласованность факторной модели путем анализа остаточной корреляционной матрицы (или остаточной дисперсионной/ковариационной матрицы). На входе можно использовать как исходные данные, так и матрицы корреляций. Подтверждающий факторный анализ и другие связанные с ним виды анализа могут быть выполнены средствами модуля Моделирование структурными уравнениями, где специальный Мастер подтверждающего факторного анализа проведет пользователя через все этапы построения модели. , проекции которого на координатные оси являются функциями координат точки M(x,y). P = P(x,y), Q = Q(x,y), то есть
, проекции которого на координатные оси являются функциями координат точки M(x,y). P = P(x,y), Q = Q(x,y), то есть  -вектор-функция. /Аналогично в пространстве/.
-вектор-функция. /Аналогично в пространстве/. задает некоторое направление;
задает некоторое направление;  получаем из P(x;y) при перемещении в направлении
получаем из P(x;y) при перемещении в направлении 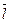 .
. f
f  - f(x;y) – приращение функции в направлении
- f(x;y) – приращение функции в направлении  l – длина отрезка PP1, величина перемещения
l – длина отрезка PP1, величина перемещения
 l
l  (1)
(1) (2)
(2) при условии, что z=f(x;y)
при условии, что z=f(x;y)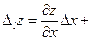



 (3)
(3) и
и 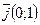 .
.
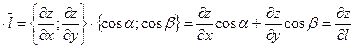

 =0
=0
 .
.


