
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Жозеф Луи Лагранж (1736-1813) – французский математик и механик
Данная теорема является обобщением теоремы Ролля Теорема. Пусть на отрезке справедлива формула
Доказательство 1. Рассмотрим вспомогательную функцию
2. Функция а) б) в) на концах отрезка 1) 2) 3. Следовательно, по теореме Ролля существует такая точка
ч.т.д. Геометрический смысл теоремы Лагранжа 1. Величина том секущей, проходящей через точки ции 2. Производная функции в точке с
3. По теореме Лагранжа Замечание 1. Равенство где
Оно называется формулой бесконечно малых приращений. Формула (4) выражает тот факт, что левая и правая части приближенного равенства равны между собой для дифференцируемой в точке «с точностью до бесконечно малых более высокого порядка, чем приращение (Так как сти по отношению к Замечание 2. 1.Так как точка
2. Учитывая это, формула (3) примет вид:
Замечание 3. Если обозначить за
Данная запись формулы Лагранжа часто бывает удобнее, чем запись в виде (3).Как будет показано далее, теорема Лагранжа лежит в основе доказательства многих формул и теорем математического анализа. Следствия к теореме Лагранжа Следствие 1. Пусть функция
Доказательство 1. Каковы бы ни были две точки 2. Следовательно, 3. По условию следствия ч.т.д. Следствие 2. Если функции Доказательство 1. Действительно, функция 2. В частности, ее производная 3. На основании следствия 1, функция ч.т.д. Следствие 3. Пусть функция
Доказательство 1. Действительно, пусть 2. Если где
3. Будем считать для определенности, что 4. Выберем 5. Поскольку 6. Применяя правило замены переменной для пределов функций, получим, что существует 7. Следовательно, существует и предел ч.т.д. Теорема Коши Теорема. Пусть функции
Доказательство 1. Докажем сначала, что
2. Теперь перейдем к доказательству формулы (5). Для этого введем вспомогательную функцию
3. Данная функция удовлетворяет всем условиям теоремы Ролля: а) б) в) имеет равные значения на концах отрезка 4. В соответствии с теоремой Ролля для 5. А
Следовательно, ч.т.д. Замечание 1. Формула (5) называется формулой Коши или обобщенной формулой конечных приращений. Замечание 2. В теореме Ролля, Лагранжа, Коши речь идет о существовании некоторой точки Модуль Тема №7 Основные теоремы дифференциального исчисления и их приложение к исследованию функций Лекция №6 1. Раскрытие неопределенностей по правилу Лопиталя. 2. Первое правило Лопиталя. Примеры. 3. Второе правило Лопиталя. 4. Примеры. 5. Другие виды неопределенностей и их раскрытие. 6. Примеры. Замечания. 7. Формула Тейлора для многочленов.
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 381; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.252 (0.031 с.) |
 определена и непрерывна функция
определена и непрерывна функция  , причем она дифференцируема в каждой точке интервала
, причем она дифференцируема в каждой точке интервала  . Тогда на этом интервале существует, по крайней мере, одна такая точка
. Тогда на этом интервале существует, по крайней мере, одна такая точка  , что будет
, что будет .
. .
. удовлетворяет всем трем условиям теоремы Ролля:
удовлетворяет всем трем условиям теоремы Ролля: ;
;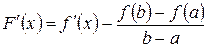 ;
; и
и  , т. е.
, т. е.  , так как
, так как ;
;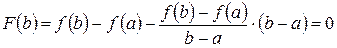 .
. , т.е.
, т.е. или
или  .
. является угловым коэффициент-
является угловым коэффициент- и
и  графика функ-
графика функ- .
.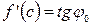 , т.е. является угловым коэффициентом касательной к графику функции в точке К
, т.е. является угловым коэффициентом касательной к графику функции в точке К  .
.
 , т.е.
, т.е.  .Значит, существует такая точка
.Значит, существует такая точка  , что касательная к графику функции
, что касательная к графику функции  в точке К
в точке К  . Причем таких точек может быть и несколько.
. Причем таких точек может быть и несколько. , (3)
, (3) или
или . (4)
. (4) функции
функции 
 при
при  ».
». – бесконечно малая функция более высокого порядка мало-
– бесконечно малая функция более высокого порядка мало-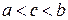 , то
, то  , где
, где  .
. , где
, где  ;
;  , то формула конечных приращений примет вид:
, то формула конечных приращений примет вид: , где
, где  .
. и
и  , принадлежащие рассматриваемому промежутку, причем
, принадлежащие рассматриваемому промежутку, причем  , функция
, функция  .
. , где
, где  .
. . Следовательно,
. Следовательно,  или
или  для любых
для любых  из рассматриваемого промежутка. Значит,
из рассматриваемого промежутка. Значит,  на указанном промежутке.
на указанном промежутке. дифференцируемы во всех внутренних точках некоторого отрезка и
дифференцируемы во всех внутренних точках некоторого отрезка и  в этих точках, а на концах отрезка функции
в этих точках, а на концах отрезка функции  .
. удовлетворяет всем условиям следствия 1.
удовлетворяет всем условиям следствия 1. во внутренних точках промежутка.
во внутренних точках промежутка. , где
, где  –
–  , является постоянной. Значит,
, является постоянной. Значит,  .
. ; дифференцируема во всех точках
; дифференцируема во всех точках  . Пусть существует предел от производной этой функции
. Пусть существует предел от производной этой функции 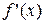 при
при  :
:  . Тогда будет существовать
. Тогда будет существовать  , причем
, причем 
 .
.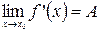 .
. и
и  ,то по теореме Лагранжа
,то по теореме Лагранжа 
 если
если  и
и  , если
, если  , откуда
, откуда
 является функцией от
является функцией от  произвольно для каждого
произвольно для каждого 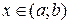 одно какое-либо значение
одно какое-либо значение  (как говорят, однозначную ветвь многозначной функции).
(как говорят, однозначную ветвь многозначной функции). , то
, то  .
. .
. . Это и означает, что производная
. Это и означает, что производная  существует и равна.
существует и равна. и
и  , и
, и  ,
, 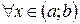 . Тогда существует такая точка
. Тогда существует такая точка  , что справедлива формула:
, что справедлива формула: . (5)
. (5) , то есть что (5) имеет смысл. Действительно, если допустить
, то есть что (5) имеет смысл. Действительно, если допустить  , то по теореме Ролля для функции
, то по теореме Ролля для функции  , в которой
, в которой  . А это противоречит условию теоремы Коши:
. А это противоречит условию теоремы Коши:  .
. .
. существует такая точка
существует такая точка  .
. и в точке
и в точке 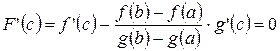 .
. . Получено требуемое равенство.
. Получено требуемое равенство.


