
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Другие виды неопределенности и их раскрытие
1. Неопределенность вида Примеры 1) Найти Решение Имеем неопределенность вида 2) Найти предел
Решение Имеем неопределенность вида
Попробуем свести к пределу типа 2. Неопределенность вида Примеры 1 ) Найти предел Решение Имеем неопределенность вида
2) Найти предел Решение Имеем неопределенность вида Но
3. Неопределенности вида
Пример. Найти предел Решение Имеем неопределенность вида Чтобы найти предел Поэтому в силу непрерывности показательной функции
Замечание 1. При многократном применении правила Лопиталя необходимо каждый раз проверять, не раскрывалась ли неопределенность, иначе можно получить ошибочный ответ, т.е. если применить правило Лопиталя к выражению, не представляющему никакой неопределенности, можно получить неверный результат. Пример. Вычислим предел функции: Если же продифференцировать числитель и знаменатель, то получим Замечание 2. По правилу Лопиталя находится предел отношения функций в том случае, когда известно существование предела отношения производных функций. Из этого не следует, что предел отношения функций не будет существовать, когда не существует предел отношения производных этих функций.
Пример. Вычислить предел функции.
Формула Тейлора для многочлена
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.211.66 (0.007 с.) |
 сводится, когда это удобно, к неопределенности типа
сводится, когда это удобно, к неопределенности типа  по схеме
по схеме  или к неопределенности вида
или к неопределенности вида  по схеме
по схеме  .
. .
.  , и получим неопределеность вида
, и получим неопределеность вида 
 .
. ,
,  .
. , и получим неопределенность вида
, и получим неопределенность вида  .
. , т.е. пришли бы к задаче вычисления более сложного предела.
, т.е. пришли бы к задаче вычисления более сложного предела. . Ее сводят к неопределенности вида
. Ее сводят к неопределенности вида  или к ее вариантам.
или к ее вариантам. .
.  к неопределенности вида
к неопределенности вида 
 .
. .
. и при том же условии
и при том же условии  получена неопределенность вида
получена неопределенность вида  применим первое правило Лопиталя
применим первое правило Лопиталя 
 .
.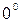 ,
,  ,
,  можно раскрыть, предварительно прологарифмировав соответствующие функции. Такие неопределенности имеют место при рассмотрении функций
можно раскрыть, предварительно прологарифмировав соответствующие функции. Такие неопределенности имеют место при рассмотрении функций  , где
, где  . Если при
. Если при  функция
функция 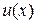 стремится соответственно к
стремится соответственно к  ;
; 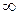 ;
;  , функция
, функция  – соответственно к
– соответственно к 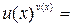
 сводятся к неопределенности вида
сводятся к неопределенности вида 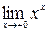 .
.  , и в показателе степени получена неопределенность вида
, и в показателе степени получена неопределенность вида  .
. .
. .
. .
.  .
. применимвторое правило Лопиталя
применимвторое правило Лопиталя  . Предел не существует, но
. Предел не существует, но  . В то время как отношение производных, равное
. В то время как отношение производных, равное  , при
, при  предела не имеет.
предела не имеет. 


