
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирование логарифмических функций
1. Логарифмическая функция у = log ax обратна к показательной функции х = ау и непрерывна при любых х > 0, а > 0, a ≠ 1. 2. Показательная функция х = ау дифференцируема и ее приращение нигде не обращается в нуль. 3. В силу теоремы о дифференцировании обратной функции следует, что и логарифмическая функция у = log ax дифференцируема в точке, т.е.
4. Так как х = ау, то формула примет вид 5. Если основание е, то 6. Из формул (1) и (2) и теоремы о дифференцировании сложной функции следует, что если функция f (x) дифференцируема в точке х и положительна, то в точке х дифференцируем и ее логарифм, причем будут справедливы формулы: а) б) Определение 10 Производная Пример. Если y = ln sin x, то Логарифмическое дифференцирование Это технический приём, основанный на следующем утверждении: Если ln (f (x)) дифференцируем в точке х 0,то и положительная функция f (x) дифференцируема в точке х 0 ,т.е. f′ (x 0) = f (x 0)∙(ln f (x 0)) ′x. Доказательство 1. Если f (x) положительная функция, то по определению логарифма можно записать: f (x) = e ln f ( x ). 2. Если натуральный логарифм функции f (x) дифференцируем в точке х 0, то в силу теоремы о дифференцировании сложной функции можно показать: (f (x)) ′x = e ln f (x)∙(ln f (x)) ′x. 3. Но e ln f ( x) = f (x), следовательно, (f (x)) ′x = f (x)∙(ln f (x)) ′x или f′ (x 0) = f (x 0)∙(ln f (x 0)) ′x [26]. ч.т.д. Дифференцирование степенно-показательных Выражений Пусть f (x) = U (x) V ( x ), причём U (x) > 0 для любых х f′ (x 0) = Доказательство 1. Так как f (x) = U (x) V ( x ), то прологарифмируем по основанию е обе части записанного равенства: ln f (x) = ln[ U (x) V ( x )] = V (x)∙ln U (x). 2. Правая часть записанного выражения дифференцируема в точке х 0: а) V (x) – дифференцируема по условию; б) ln U (x) дифференцируем в точке х 0, так как положительная функция U (x) дифференцируема в точке х 0 по условию, а следовательно, дифференцируем и ln U (x) в точке х 0 на основании теоремы о дифференцировании сложной функции в точке. 3. Тогда по правилам дифференцирования произведения функций в точке получим: (ln f (x)) ′x =
4. Так как существует производная правой части выражения в точке х 0, то существует и производная левой части выражения в точке х 0, т.е. существует производная логарифма функции f (x) в точке х 0, а значит, существует и производная функции f (x) в точке х 0 на основании логарифмического дифференцирования, т.е. (ln f (x 0)) ′x =
f′ (x 0) = f (x 0) f′ (x 0) = Или без обозначения аргументов: f′ = UV ∙ f′ = UV∙V′∙ ln U + UV -1∙ V ∙ U′. (٭) ч. т.д. Замечание Эту формулу легко запомнить, заметив, что первое слагаемое правой части получается дифференцированием UV как показательной функции с постоянным основанием, т.е. U – const (ах); а второе – как степенной функции с постоянным показателем степени, т.е. V – const (хn). Пример. Если у = хх, то у′х = хx ∙ln x ∙1 + x ∙ xx -1 = хх ∙(ln x + 1) [26]. Производные высших порядков Определение 11 f′ (х) называется первой производной функции f (х) в точке х. Определение 12 Производная от первой производной некоторой функции в точке называется производной второго порядка или второй производной. Определение 13 Производная от второй производной называется производной третьего порядка или третьей производной и т.д. Определение 14 Производные, начиная со второй, называются производными высшего порядка и обозначаются: Определение 15 Производная n -ого порядка есть производная от производной (n -1)-ого порядка, так как Модуль Тема №6
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 620; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.30.253 (0.009 с.) |
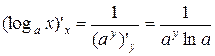 .
. . (1)
. (1) . (2)
. (2) ;
;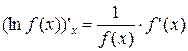 .
. [
[  ] называется логарифмической производной функции f (x) в точке х.
] называется логарифмической производной функции f (x) в точке х. [4].
[4]. D (f (x)). Если функции U (x) и V (x) дифференцируемы в точке х 0, то и функция f (x) дифференцируема в точке х 0, причём верна формула:
D (f (x)). Если функции U (x) и V (x) дифференцируемы в точке х 0, то и функция f (x) дифференцируема в точке х 0, причём верна формула: .
. .
. , следовательно,
, следовательно, , тогда,
, тогда,
 ] или
] или или
или  .
. [26].
[26].


