Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные высших порядков от обратных
Функций Теорема Пусть функция у = f (х) непрерывна и строго монотонно в некоторой окрестности точки х 0. Пусть в точке х = х 0 существуют производные у' (х 0) и у'' (х 0), причем у' (х 0) ≠ 0. Тогда существует обратная функция х = φ (у), и она имеет вторую производную в точке у 0= f (х 0), причем справедлива формула:
Доказательство 1. На основании теоремы о производной обратной функции имеем:
2. Вычислим от обеих частей последнего равенства производную по переменной у с учётом правила дифференцирования сложной функции и частного двух функций. 3. Получим
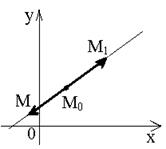
или (x′y) ′y = ч.т.д. Параметризованные пути. Кривая Жордано Определение 16 Параметризацией множества Е называется всякое отображение какого-либо множества F на Е. При этом общий элемент множества F на Е называется параметром, конкретные элементы – значения параметра и говорят, что множество Е параметризовано множеством F посредством отображения f. Определение 17 Параметризованным путём в плоскости называется всякое множество точек, параметризованные каким-либо невырожденным промежутком. Таким образом, параметризованный путь в плоскости определяется заданием отображения р:®П, областью определения которого является некоторый невырожденный промежуток I. Часто параметризованным путём называют само отображение р. Определение 18 Параметризованный путь, определённый непрерывным отображением р невырожденного промежутка в плоскость, называется кривой Жордано. Если р – координатная плоскость, то точки параметризованного пути получают представление вида: р(t) = M(φ(t);ψ(t)), где φ и ψ – компоненты отображения р, и мы приходим к параметрическим уравнениям: х = φ(t), у = ψ(t). Пример 1 Параметрическое уравнение прямой. Пусть L – прямая, проходящая через две точки М0(х0;у0) и М1(х1;у1). Её можно задать уравнением: (у1-у0)(х-х0) – (х1-х0)(у-у0) = 0. Действительно, так как М1 ≠ М0, то хотя бы один из коэффициентов у1-у0, х1-х0 показала, что эта прямая, проходящая через точки М1 и М0, т.е. совпадает с L. Покажем, что L можно задать параметрическими уравнениями х = (1-t)х0+tx1, у=(1-t)y0 + ty1, (-∞<t<+∞). Действительно, точка М1 представима в виде (х-х0) = (х1-х0)t, (у-у0) = (у1-у0)t. Умножая первое из уравнений на (у1-у0), второе на (х1-х0) и вычитаем, видим, что каждая точка параметрического пути принадлежит L.
Обратно: всякая точка М(х,у), принадлежащая L, удовлетворяет уравнениям при t = (х-х0)/(х1-х0) (если х1≠х0), совпадающее со значением (у-у0)/(у1-у0) (если у1≠у0) и только при нём. Это показывает, что t – есть ни что иное, как отображение коллинеарных векторов М0М:М0М1 (рис.4). В частности, когда t пробегает отрезок [0,1], точка М пробегает отрезок М0М1 прямой L. Таким образом, х = (1-t)х0 + tx1, у=(1-t)y0 + ty1, 0<t<1- уравнение отрезка М0М1. Определение 19 Пусть р – отображение невырожденного промежутка I в плоскость П, причём: 1) р непрерывна в точке t0, т.е. существует такая окружность U точки t0, что р(t) ≠ р(t0) для всех t
Рис.4. Рис.5.
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 798; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.147 (0.004 с.) |
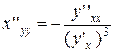 или
или 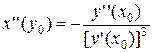 .
.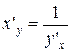 , y′x ≠ 0 в точке х 0. (
, y′x ≠ 0 в точке х 0. ( ).
).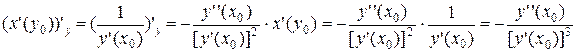
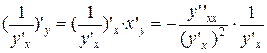 [17].
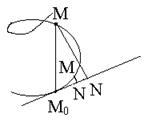
[17].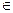 (U/{t0})∩I. Касательной к параметризованному пути р в его точке М0 = р(t) называют такую прямую L, проходящую через М0, что расстояние MN от точки М = р(t) до этой прямой бесконечно мало по сравнению с М0М при t→t0. (рис.5)
(U/{t0})∩I. Касательной к параметризованному пути р в его точке М0 = р(t) называют такую прямую L, проходящую через М0, что расстояние MN от точки М = р(t) до этой прямой бесконечно мало по сравнению с М0М при t→t0. (рис.5)