Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейной модели парной регрессииСодержание книги
Поиск на нашем сайте
Расчет коэффициентов уравнения регрессии на основе данных табл.2.2:
Вывод. Линейная регрессионная модель связи изучаемых признаков имеет вид уравнения
Коэффициент регрессии
3. Проверка уравнения регрессии на адекватность [2]. 1. Оценка практической пригодности построенной модели связи
Расчет R2:
Вывод. Критерий практической пригодности модели связи R2 > 0,5 не выполняется. Однако поскольку значение R2 практически совпадает с 0,5, можно считать, что построенное регрессионное уравнение в достаточной мере отражает фактическую зависимость признаков и пригодно для практического применения.
2. Оценка статистической значимости (неслучайности) коэффициента R2по F-критерию Р.Фишера рассчитывается по формуле:
где m – число коэффициентов уравнения регрессии (параметров уравнения регрессии), n- число наблюдений. Расчет значения F при n=30, m=2:
Табличное (критическое) значение F -критерия Fтабл имеет общий вид
Так как Fрасч>Fтабл, то величина найденного коэффициента детерминации R2.признается неслучайной с вероятностью 0,95. Вывод. Построенное уравнение регрессии можно считать адекватным с надежностью 95%. Расчет коэффициента эластичности
Вывод. Величина коэффициента эластичности
Задание 3. Применение выборочного метода в статистическом исследовании. По результатам выполнения задания 1 с вероятностью 0,954 определите: 1) ошибку выборки средней величины выручки от продажи продукции и границы, в которых будет находиться средняя величина выручки предприятий генеральной совокупности. 2) ошибку выборки доли предприятий с выручкой от продажи продукции более 250 млн. руб. и границы, в которых будет находиться генеральная доля. Значения параметров, необходимых для решения задачи и рассчитанных в задании 1, представлены в табл. 3.1: Таблица 3.1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 108; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.5.216 (0.006 с.) |

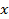


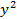
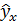
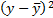
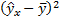
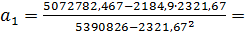 0,245
0,245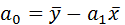 = 2184,9-0,245∙2321,67=1616,091
= 2184,9-0,245∙2321,67=1616,091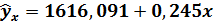
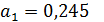 показывает, что при увеличении факторного признака Выручка от продажи продукции на 1 млн руб. значение результативного признака Прибыль от продажи продукции увеличивается в среднем на
показывает, что при увеличении факторного признака Выручка от продажи продукции на 1 млн руб. значение результативного признака Прибыль от продажи продукции увеличивается в среднем на 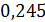 млн руб.
млн руб.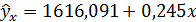 по величине коэффициента детерминации R2.
по величине коэффициента детерминации R2.
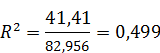
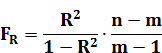
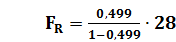 = 27,888
= 27,888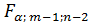 , где
, где  - уровень значимости, m– число коэффициентов уравнения регрессии. При уровне значимости
- уровень значимости, m– число коэффициентов уравнения регрессии. При уровне значимости 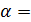 0,05 и m=2
0,05 и m=2
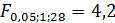
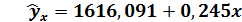
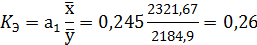
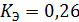 показывает, что при увеличении факторного признака Выручка от продажи продукции на 1% значение результативного признака Прибыль от продажи продукции увеличивается в среднем на 0,26%.
показывает, что при увеличении факторного признака Выручка от продажи продукции на 1% значение результативного признака Прибыль от продажи продукции увеличивается в среднем на 0,26%.