
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Департамент учета, анализа и аудитаСодержание книги
Поиск на нашем сайте
Департамент учета, анализа и аудита
Расчетно - аналитическая работа
по дисциплине «Статистика»
Исполнитель: Давыдов Д.В. Факультет: ИЗОО Направление: Экономика Группа: ДЭБ1-2В № зачетной книжки: 165466 Руководитель: Кожевникова Г.П.
Москва 2016 Задание 1. Исследование структуры изучаемой статистической совокупности. Исходные данные: При N = i * к*l = 16*66*2=2112 Таблица 1.1 Исходные данные задания
По исходным данным таблицы 1.1: 1) постройте статистический интервальный ряд распределения предприятий по признаку «Выручка от продажи продукции», образовав пять групп с равными интервалами; 2) рассчитайте значения моды и медианы полученного интервального ряда распределения; 3) рассчитайте следующие статистические характеристики ряда распределения: среднюю арифметическую, дисперсию, среднее квадратическое отклонение, коэффициент вариации, представив расчеты в табличном виде. Сделайте выводы по результатам выполнения пунктов 1 - 3. Построение интервального ряда распределения Расчет величины h и границ интервалов ряда:
( Границы интервалов ряда распределения приведены в табл.1.2. Таблица 1.2 Границы интервалов ряда распределения
Интервальный ряд распределения предприятий по величине выручки от продажи продукции представлен в виде табл. 1.3. Таблица 1.3. Распределение предприятий по размеру Выручки от продажи продукции
Вывод. Анализ интервального ряда распределения изучаемой совокупности предприятий показывает, что распределение предприятий по размеру выручки от продажи продукции не является равномерным: преобладают предприятия с размером выручки от 2306 млн руб. до 2330 млн руб. (это 14 предприятий, доля которых составляет 46,7 %); 22 предприятия имеют размер выручки не более 2330 млн руб., а 26 - не более 2354 млн руб.
Задание 2. Корреляционно-регрессионный анализ взаимосвязи между признаками совокупности. По исходным данным (табл.1.1) с использованием результатов выполнения задания 1: 1) методом аналитической группировки установите наличие и направление корреляционной связи между факторным признаком Х - «Выручка от продажи продукции» и результативным признаком Y - «Прибыль от продажи продукции»; 2) по исходным данным постройте линейную однофакторную регрессионную модель зависимости признака Y от фактора Х; 3) проверьте найденную модель на адекватность; 4) рассчитайте средний коэффициент эластичности взаимосвязи признаков. Сделайте выводы по результатам выполнения задания. 1. Применение метода аналитической группировки для установления наличия и направления связи между признаками Выручка от продажи продукции и Прибыль от продажи продукции
На основе первичных данных (табл. 1.1) взаимосвязь между изучаемыми признаками графически отображается в виде поля корреляции (рис. 2.1).
 
Рис.2.1. Поле корреляции взаимосвязи изучаемых признаков.
Как видно из рис.2.1, наблюдается не беспорядочное рассеивание точек по полю, а достаточно четкая их концентрация (корреляционное облако). Так как точки распределяются от нижнего левого угла поля в сторону верхнего правого, можно предположить, что между признаками имеется связь и она прямая.
Для того, чтобы определить, является ли связь корреляционной [1], применяется метод аналитической группировки по фактору Х (используется ряд распределения табл.1.3). Аналитическая таблица для анализа корреляционной связи между факторным признаком Х - «Выручка от продажи продукции» и результативным признаком Y - «Прибыль от продажи продукции» имеет следующий вид: Таблица 2.1 Задание 3. Применение выборочного метода в статистическом исследовании. По результатам выполнения задания 1 с вероятностью 0,954 определите: 1) ошибку выборки средней величины выручки от продажи продукции и границы, в которых будет находиться средняя величина выручки предприятий генеральной совокупности. 2) ошибку выборки доли предприятий с выручкой от продажи продукции более 250 млн. руб. и границы, в которых будет находиться генеральная доля. Значения параметров, необходимых для решения задачи и рассчитанных в задании 1, представлены в табл. 3.1: Таблица 3.1
Задание 4. Методы анализа рядов динамики в экономических задачах. Задание 4.1. Расчёт и анализ основных показателей ряда динамики. При N = i * к*l = 16*66*2=2112 Исходные данные варианта задания представлены в табл. 4.1, результаты анализа ряда динамики - в табл.4.2. Таблица 4.1 Задание 4.2. Расчёт и анализ средних показателей ряда динамики
1. Среднегодовой объем реализации продукции:
2.Среднегодовой абсолютный прирост объемов реализации продукции:
3. Среднегодовой темп роста объемов реализации продукции:
4. Среднегодовой темп прироста объемов реализации продукции:
Вывод. За исследуемый период средний объем реализации произведенной продукции составил 49785,3 тыс. тонн. Выявлена положительная динамика реализации продукции: ежегодное увеличение объема реализации составляло в среднем
График динамики объемов реализации продукции представлен на рис.4.1.
Рис. 4.1. Динамика объемов реализации продукции за пятилетний период Задание 4.3. Выявление тенденции развития изучаемого явления 1. Сглаживание ряда динамики методом укрупнения интервалов Результаты представлены в табл.4.3. Таблица 4.3. Расчётная таблица для определения укрупнённых (поквартальных) данных
Вывод. Данные табл. 4.3 показывают, что в результате применения метода укрупнения интервалов проявилось общее направление (тренд) изменения объема реализации продукции: в первых трех кварталах среднемесячные объемы реализации продукции возрастали, а в четвертом существенно снизились.
2. Сглаживание ряда динамики методом скользящих средних Результаты представлены в табл.4.4. Таблица 4.4 Расчётная таблица для определения значений скользящей средней
Вывод. Как показывают данные табл.4.4, значения скользящей средней до сентября месяца почти систематически возрастали, а затем стали снижаться, что свидетельствует об общей параболической тенденции изменения объемов реализации продукции. Поскольку большая часть параболы близка к прямолинейной форме (7 значений скользящей средней из 10-ти систематически возрастают), для сглаживания ряда динамики может быть использовано выравнивание ряда по прямой (а не по параболе). 3. Аналитическое выравнивание ряда динамики по прямой 3.1.Аналитическое уравнение прямой имеет вид:
где t – порядковый номер периодов (или моментов) времени;
Отсчёт времени удобно производить так, чтобы сумма показателей времени ряда динамики была равна нулю[3]:
параметры уравнения определяются по формулам:
Расчет значений величин
Таблица 4.5 Расчетная таблица для определения параметров
Использование итоговых данных гр. 2-5 табл.4.5 дает систему нормальных уравнений
Из 1-го уравнения определяется значение
Вывод. Уравнение прямой для сглаживания динамического ряда:
3.2. Проверка правильности расчёта уровней выровненного ряда динамики (сумма значений уровней эмпирического ряда (гр.2) должна совпадать с суммой значений уровней выровненного ряда (гр.6)): 55187,4 = 55187,4 3.3. Графики эмпирической и сглаживающей кривых представлены на рис.4.2.
Рис. 4.2. Сглаживание ряда динамики объемов реализации продукции методом аналитического выравнивания по прямой
4.4. Прогнозирование значений показателей методом экстраполяции [4] 1. Прогнозирование уровня ряда динамики с использованием среднего абсолютного прироста осуществляется по следующей формуле:
где: t – период упреждения (число лет, кварталов и т.п.);
Прогнозируемый объем реализации продукции на 7 год (по данным пятилетнего периода) с использованием среднего абсолютного прироста, рассчитанного в задании 4.2:
2. Прогнозирование уровня ряда динамики с использованием среднего темпа (коэффициента) роста осуществляется по следующей формуле:
где Прогнозируемый объем реализации продукции на седьмой год (по данным пятилетнего периода) с использованием среднего темпа роста, рассчитанного в задании 2:
3. Прогнозирование объемов реализации продукции методом аналитического выравнивания ряда динамики по прямой Модель прямолинейной зависимости уровня ряда от фактора времени имеет следующий вид:
Расчет значений величин Таблица 4.6 Вспомогательная таблица для расчёта параметров тренда
По системе уравнений определяем значение параметров
Расчет теоретических уровней приведен в гр.6. Совпадение итоговых значений гр.2 и 6 указывает на правильность расчётов уровней выровненного ряда динамики. Прогнозируемый объем реализации продукции на 7 год (по данным пятилетнего периода) методом аналитического выравнивания ряда динамики по прямой:
Вывод. Как показывают полученные прогнозные данные, все прогнозируемые объемы реализации продукции на 7 год (по данным пятилетнего периода) довольно близки между собой:
Задание 5. Применение индексного метода в анализе статистических данных. Задача 5.1 При N = i * к*l = 16*66*2=2112 Имеются данные о продаже условного товара "А" в магазинах города в третьем и четвертом кварталах(табл.5.1). Таблица 5.1 Исходные данные
Определите: 1. По каждой форме торговли относительные изменения (индивидуальные индексы): - цен, - физического объема продажи (в натуральном выражении). 2. В целом по двум формам торговли относительные изменения (общие индексы): - цен (в форме Пааше), - физического объема продажи (в форме Ласпейреса), - товарооборота (в стоимостном выражении). Покажите взаимосвязь между этими индексами. 3. Абсолютное изменение товарооборота - общее и в результате влияния отдельных факторов (изменения цен и изменения физического объема продаж). 4. Индексы средней цены товара "А" переменного и постоянного состава, индекс влияния структурных сдвигов в объеме продаж. Покажите взаимосвязь индексов переменного, постоянного состава и структурных сдвигов. 5. Изменение средней цены товара "А" в абсолютном выражении и влияние на это изменение двух факторов: а) изменение цен, б) изменение структуры объемов продажи. Результаты промежуточных расчетов представьте в табличной форме. Сделайте выводы.
1. Расчет индивидуальных индексов 1.1 Для определения относительного изменения цены товара (p) по каждой форме торговли необходимо рассчитать индивидуальные индексы цен (ip) по формуле
где p0 и p1 – цена товара в базисном и отчетном периодах. Расчет индивидуальных индексов цен по формуле (5.1): - сетевая торговля: - несетевая торговля:
Вывод. В сетевой торговле цена на товар «А » выросла в IV кв. по сравнению с III кв. на 75% (175-100), что в абсолютном выражении составляет 30 руб.(70-40), в несетевой - на 67% или на 20 руб.
1.2. Для определения относительного изменения объема продажи товара (q) необходимо рассчитать индивидуальные индексы физического объема (iq) по формуле
где q0 и q1 – количество (физический объем) товара, реализованного в базисном и отчетном периодах. Расчет индивидуальных индексов физического объема по формуле (5.2): - сетевая торговля: - несетевая торговля: Вывод. В сетевой торговле объем продажи товара «А» вырос в IV кв. по сравнению с III кв. на 7,5% (107,5-100), что в абсолютном выражении составляет 0,366 тыс.кг, в несетевой - на 14% или на 0,788 тыс.кг.
2. Расчет общих индексов относительного изменения товарооборота Для расчета общих индексов сформируем табл.5.2. В графах 2 - 5 запишем исходные данные, в графах 6 и 7 - рассчитанные индивидуальные индексы, в графах 8 - 11 - товарооборот в разных периодах. Таблица 5.2
Расчетная таблица
2.1. Расчет общего индекса цен. Индекс цен, характеризующий относительное изменение товарооборота под влиянием изменения цен, рассчитывается по формуле
Расчет общего индекса цен по формуле
Вывод. В целом по двум формам торговли цена товара возросла в IV кв. по сравнению с III кв. в среднем на 71%. Абсолютная сумма перерасхода денежных средств населения в результате повышения цены товара "А" составляет 284,77 тыс.руб. (685,87 – 401,1).
2.2. Расчет общего индекса физического объема продаж. Индекс физического объема продаж, показывающий относительное изменение товарооборота под влиянием изменения объема продаж, рассчитывается по формуле
Расчет общего индекса физического объема продаж по формуле
Вывод. В целом по двум формам торговли объем продаж товара возрос в IV кв. по сравнению с III кв. в среднем на 10,6%.
2.3. Расчет общего индекса товарооборота. Индекс товарооборота, характеризующий относительное изменение товарооборота под влиянием изменения двух факторов - цен и физического объема продаж, рассчитывается по формуле
Расчет общего индекса товарооборота по формуле
Вывод: в целом по двум формам торговли товарооборот в IV кв. по сравнению с III кв. в результате изменения цен и физического объема продаж увеличился на 89 %, что в абсолютном выражении составляет 323,12 тыс. руб.
2.4. Взаимосвязь индексов и разложение изменения товарооборота по факторам
Произведение индекса физического объема и индекса цен должно давать индекс изменения товарооборота (мультипликативная связь), т.е.
Эта формула называется факторной моделью индекса товарооборота. Она показывает изменение товарооборота за счёт изменения цен и за счёт изменения объема продаж. Разложение относительного изменения товарооборота по факторам:
Вывод. В целом по двум формам торговли увеличение товарооборота в 1,89 раз произошло за счет роста цены товара в 1,71 раза и роста объема продаж в 1,106 раза.
3. Определение абсолютного изменения товарооборота. Общее абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным (под влиянием обоих факторов) определяется какразностьмежду числителем и знаменателем индекса товарооборота (5.5):
Разность между числителем и знаменателем индекса цен (5.3) характеризует абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным в результате изменения цен:
Разность между числителем и знаменателем индекса физического объемапродаж (5.4) характеризует общее абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным в результате изменения физического объема продаж:
Взаимосвязь абсолютных приростов (аддитивная связь):
Эта формула называется аддитивноймоделью индекса товарооборота. Она показывает абсолютное изменение товарооборота за счёт изменения цен и за счёт изменения объема продаж. 3.1. Расчет абсолютного изменения товарооборота в отчетном периоде по сравнению с базисным: - общего абсолютного изменения по формуле (5.7):
- под влиянием изменения цен по формуле (5.8):
- под влиянием изменения физического объема продаж по формуле (5.9):
3.2. Разложение абсолютных приростов товарооборота по факторам (5.10):
Вывод. В целом по двум формам торговли товарооборот в IV кв. по сравнению с III кв. под влиянием изменения цены товара (на 71%) вырос в среднем на Задача 5.2 Исходная информация представлена в табл.5.4. Требуется определить относительное изменение физического объема товарооборота в целом по двум видам товара. Таблица 5.4 Исходные данные
Для определения относительного изменения физического объема товарооборота обычно рассчитывают агрегатный индекс физического объема товарооборота
Однако, по приведенной в табл.5. 4 исходной информации этого сделать нельзя, так как неизвестен товарооборот отчетного периода в базисных ценах (числитель индекса Для преобразования используют формулу индивидуального индекса физического объема[5], получая средний арифметический взвешенный индекс физического объема товарооборота (5.21 ):
где
1. Расчет индивидуальных индексов физического объема (количества) реализованного товара: Товар А: Товар В: (результаты расчетов представлены в расчетной табл.5.5, гр.4, 5). Таблица 5.5 Расчетная таблица
2. Расчет среднего арифметического индекса физического объема по формуле (5.21):
Вывод. О бъем продажи разнородных товаров (физический объем товарооборота) вырос в отчетном периоде по сравнению с базисным в среднем на 39,7% (139,7 - 100).
Разность между числителем и знаменателем индекса физического объема характеризует сумму экономии, полученную в результате увеличения физического объема продаж товаров:
Задача 5. 3 Исходная информация представлена в табл.5.6 Требуется определить относительное изменение уровня цен в целом по двум видам товара.
Таблица 5.6 Исходные данные
Для изучения относительного изменения уровня цен на разнородные товары в отчетном периоде по сравнению с базисным периодом обычно рассчитывают агрегатный индекс цен по формуле (5.3):
Однако по исходным данным, приведенным в табл.5.5, такой индекс рассчитан быть не может, так как отсутствуют данные о товарообороте отчетного периода в базисных ценах (знаменатель индекса
В результате преобразования получают средний гармонический взвешенный индекс цен:
где
1. Расчет индивидуальных индексов цен по каждому виду товара: Товар А: Товар Б: (результаты расчетов представлены в гр.4 табл.5.7). Таблица 5. 7 Таблица для расчета среднего гармонического индекса цен
|

 =
=  млн руб.
млн руб. – наибольшее и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда).
– наибольшее и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда).
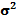


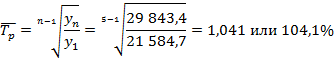
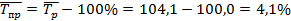
 тыс. тонн или 4,1%.
тыс. тонн или 4,1%.

 – выровненные значения ряда динамики.
– выровненные значения ряда динамики.
 При соблюдении принципа отсчёт а времени t от условного нулевого начала система нормальных уравнений имеет вид:
При соблюдении принципа отсчёт а времени t от условного нулевого начала система нормальных уравнений имеет вид:

 ,
, 
 ,
,  и
и  приведен в табл.4.5
приведен в табл.4.5 уравнения прямой
уравнения прямой






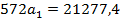
 , из 2-го -
, из 2-го -  :
: = 4598,95
= 4598,95  = 37,20
= 37,20


 – прогнозируемый уровень;
– прогнозируемый уровень; – конечный уровень ряда динамики;
– конечный уровень ряда динамики; – средний за исследуемый период абсолютный прирост (среднегодовой, среднеквартальный и т.п.).
– средний за исследуемый период абсолютный прирост (среднегодовой, среднеквартальный и т.п.).

 – средний за исследуемый период темп роста (среднегодовой, среднеквартальный и т.п.).
– средний за исследуемый период темп роста (среднегодовой, среднеквартальный и т.п.).

 Параметры уравнения a и b определяются путем решения системы нормальных уравнений:
Параметры уравнения a и b определяются путем решения системы нормальных уравнений:

 ,
,  ,
,  и
и  приведен в табл.4.6.
приведен в табл.4.6.
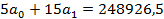

 и
и  , уравнение прямой имеет вид:
, уравнение прямой имеет вид:
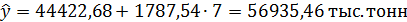
 ,
,  и
и  тыс. тонн. Расхождение полученных данных объясняется тем, что в основу прогнозирования положены разные методики экстраполяции рядов динамики.
тыс. тонн. Расхождение полученных данных объясняется тем, что в основу прогнозирования положены разные методики экстраполяции рядов динамики. , (5.1)
, (5.1)
 166,7%
166,7%













 :
:

 :
:
 (5.5)
(5.5)

 (5.6)
(5.6)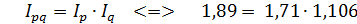
 (5.7)
(5.7) (5.8)
(5.8) (5.9)
(5.9) (5.10)
(5.10)


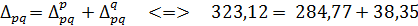
 Рост физического объема продаж на 10,6% привел к увеличению товарооборота в среднем н
Рост физического объема продаж на 10,6% привел к увеличению товарооборота в среднем н  Совместное влияние двух факторов выразилось в росте общего товарооборота в среднем на
Совместное влияние двух факторов выразилось в росте общего товарооборота в среднем на  . (на 89%).
. (на 89%).
 .
. ). Он может быть рассчитан на основе данных гр. 4 с использованием преобразования агрегатного индекса физического объема в средний арифметический взвешенный:
). Он может быть рассчитан на основе данных гр. 4 с использованием преобразования агрегатного индекса физического объема в средний арифметический взвешенный: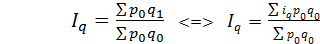
 (5.21)
(5.21) – индивидуальный индекс физического объема;
– индивидуальный индекс физического объема; – стоимость реализованных товаров (товарооборот) в базисном периоде.
– стоимость реализованных товаров (товарооборот) в базисном периоде.
 =100+66,7=166,7 %, или 1,667;
=100+66,7=166,7 %, или 1,667;

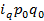



 Он может быть рассчитан на основе данных гр.4 с использованием преобразования агрегатного индекса цен в средний гармонический взвешенный [6]:
Он может быть рассчитан на основе данных гр.4 с использованием преобразования агрегатного индекса цен в средний гармонический взвешенный [6]:
 (5.22)
(5.22) – индивидуальный индекс цен;
– индивидуальный индекс цен; – стоимость реализованных товаров (товарооборот) в отчетном периоде.
– стоимость реализованных товаров (товарооборот) в отчетном периоде. = 100+10=110,0%, или 1,100;
= 100+10=110,0%, или 1,100;


