
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двумерные массивы. Вложенные циклы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: Приобрести опыт работы с двумерными массивами. Изучить организацию вложенных циклов с.
Краткие теоретические сведения Многомерные массивы имеют два и более индексов. Сооответственно каждый элемент двумерного массива (матрицы) имеет два индекса: номер строки – i; номер столбца – j. Для обработки матриц организуют два цикла, причем один вкладывается в другой. Такие циклы называются вложенными или циклами в цикле. При этом параметром в каждом цикле будет соответствующий индекс элемента массива. Для составления алгоритма и программы необходимо определить, как они меняются. Если значениями параметра первого цикла будут номера строк матрицы, то значениями параметра второго – столбцы (или наоборот). Двумерный массив можно представить так: d11 d12... d1n d12 d22... d2n D =....... ....... dm1 dm2... dmn
Объявление матриц
Двумерный массив, как и любая переменная программы, перед использованием должен быть объявлен в разделе описания переменных. В общем виде инструкция объявления массива выглядит следующим образом: Имя: array [нижний_индекс_строки..верхний_индекс_строки, нижний_индекс_столбца…верхний_индекс_столбца] of тип; где: имя — имя массива; array — зарезервированное слово языка Delphi, обозначающее, что объявляемое имя является именем массива; нижний_индекс_строки (столбца) и верхний_индекс_строки (столбца) — целые константы, определяющие диапазон изменения индекса строк (столбцов) элементов матрицы и, неявно, количество элементов (размер) матрицы; тип — тип элементов двумерного массива (базовый тип). Так же двумерный массив можно описать так: array[ нижний_индекс_строки.. верхний_индекс_строки ] of array[ нижний_индекс_столбца.. верхний_индекс_столбца ] of тип;
Примеры объявления двумерных массивов: temper:array[1..3, 1..4] of real; M1: array[1..3] of array[1..3] of Byte; name:array[1..30,1...8] of string[25]; Приведем пример объявления с помощью константы двумерного массива, состоящего из 12 элементов типа Integer: const n=4; m=3; var a:array [1..n, 1..m] of integer; Существует еще один способ объявления массивов: Имя_массива: array [нижний_индекс..верхний_индекс] of тип; Имя_матрицы: array[нижний_индекс..верхний_индекс] of имя_массива; Для того чтобы в программе использовать элемент матрицы, надо указать имя матрицы и индексы элемента, заключив индексы в квадратные скобки и отделив их запятой. В качестве индексов можно использовать константу или выражение целого типа, например: a[1,2]:=4; d:=a[2,1]+a[3,2]; ShowMessage(name[n,m]); temper[i,j]:= StrToFloat(Edit1.text); Индексы не должены выходить за пределы диапазона, указанного в описании двумерного массива в квадратных скобках.
Инициализация двумерного массива Если двумерный массив не является локальным, т. е. объявлен не в процедуре обработки события, а в разделе переменных модуля, то одновременно с объявлением массива можно выполнить его инициализацию, т. е. присвоить начальные значения элементам массива. Инструкция объявления массива с одновременной его инициализацией в общем виде выглядит так: Имя:array [нижний_индекс_строки..верхний_индекс_строки, нижний_индекс_столбца..верхний_индекс_столбца] of тип = (список); где список — разделенные запятыми значения элементов массива. Например: a: array[1...2,1..5] of integer = (0,1,2,3,4 5, 6, 7, 8, 9); Обратите внимание, что количество элементов списка инициализации должно соответствовать размерности массива. Если это будет не так, то компилятор выведет cообщение об ошибке: Number of elements differs from declaration (количество элементов не соответствует указанному в объявлении). При попытке инициализировать локальный массив компилятор выводит сообщение об ошибке: Cannot initialize local variables (локальная переменная не может быть инициализирована). Локальный массив можно инициализировать только во время работы программы, например, так: for i:= 1 to 2 do for j:= 1 to 5 do a[i[][j]:= i+2
Задание к выполнению лабораторной работы Задание А Выбрать алгоритм, составить его блок-схему и программу, в ко- торой: 1) разбив отрезки [a; b] и [c; d] соответственно на n и m частей, в точ- ках xi = a + (i – 1)×h1, yj = c + (j – 1)×h2, где h1 = (b – a)/n, h2 = (d – c)/m, i = 1, 2, …, n+1, j = 1, 2, …, m+1 вычислить значения элементов aij матрицы A =||aij||nm по формуле aij = z(xi, yj), где z = z(x, y) – функция, заданная в варианте задания; из элементов матрицы А составить матрицу В так, чтобы в ней элементы строк матрицы А располагались в порядке возрастания. Указанным в варианте задания способом найти вектор (матрицу, строку) X;
Задание Б Составить блок-схему и написать программу для решения приведенной в варианте задания задачи. Предусмотреть возможность ввода элементов массива с клавиатуры и из файла, а также возможность сохранения в файл.
Содержание отчета 6. Тема, цель лабораторной работы и постановка задания в соответствии с вариантом. 7. Схематичное изображение главной формы приложения для заданий Б и В. 8. Блок-схемы. 9. Тексты программ. 10. Ответы на контрольные вопросы. Варианты заданий Задание А
Задание В
1. Вычислить сумму и число отрицательных элементов матрицы А, находящихся под главной диагональю. Элементы матрицы вычисляются по формуле 2. Вычислить сумму и число положительных элементов матрицы А, находящихся под главной диагональю. Элементы матрицы вычисляются по формуле 3. Вычислить сумму и число положительных элементов матрицы А, находящихся на главной диагонали. Элементы матрицы вычисляются по формуле 4. Вычислить сумму и число положительных элементов матрицы А. Элементы матрицы вычисляются по формуле 5. Вычислить сумму и число отрицательных элементов матрицы А, находящихся над главной диагональю. Элементы матрицы вычисляются по формуле 6. Вычислить сумму и число отрицательных элементов матрицы А, находящихся под главной диагональю. Элементы матрицы вычисляются по формуле 7. В матрице А положительные элементы заменить на нули и ре- зультаты записать в матрицу В. Вычислить число и сумму отрицатель- ных элементов в матрице В. Элементы матрицы А вычисляются по формуле
8. В матрице А отрицательные элементы заменить на единицы и ре- зультаты записать в матрицу В. Вычислить число и сумму отрицатель- ных элементов в матрице В. Элементы матрицы А вычисляются по фор- муле 9. В матрице А отрицательные элементы заменить на нули, а положительные на единицы и записать результат в матрицу В. Вычислить число элементов, равных единице в матрице В. Элементы матрицы А вычисляются по формуле 10. В каждой строке матрицы А найти минимальный элемент. Элементы матрицы А вычисляются по формуле 11. В каждом столбце матрицы А найти максимальный элемент. Элементы матрицы А вычисляются по формуле 12. Транспонировать матрицу А и результат записать в матрицу В. Вычислить сумму индексов положительных элементов матрицы В, стоящих на главной диагонали. Элементы матрицы А вычисляются по формуле 13. В матрице А найти число строк и столбцов, содержащих более трех отрицательных элементов, и их номера. Элементы матрицы А вы- числяются по формуле 14. В матрице А найти число строк и столбцов содержащих не более трех положительных элементов, и их номера. Элементы матрицы А вы- числяются по формуле 15. В целочисленной матрице А найти сумму и число элементов кратных пяти. Элементы матрицы А вычисляются по формуле
16. В целочисленной матрице А найти номера строк, содержащих более трех четных элементов. Элементы матрицы А вычисляются по формуле 17. В целочисленной матрице А найти номера строк, содержащих более трех четных элементов, кратных трем. Элементы матрицы А вы- числяются по формуле 18. В целочисленной матрице А найти сумму четных элементов. Элементы матрицы А вычисляются по формуле 19. В целочисленной матрице А найти сумму элементов кратных че- тырем. Элементы матрицы А вычисляются по формуле
20. В целочисленной матрице А найти сумму индексов четных элементов. Элементы матрицы А вычисляются по формуле
21. В каждой строке матрицы А найти максимальный элемент и по- менять его местами с первым элементом соответствующей строки. Эле- менты матрицы А вычисляются по формуле 22. В каждой строке матрицы А найти минимальный элемент и по- менять его местами с последним элементом соответствующей строки. Элементы матрицы А вычисляются по формуле i, j = 1, 2, …, 10. 23. Найти наименьший и наибольший элементы матрицы А и поме- нять их местами. Результат записать в матрицу В. Элементы матрицы вычисляются по формуле 24. В каждой строке матрицы А найти наименьший элемент и поме- нять его местами с соответствующим элементом главной диагонали. Элементы матрицы А вычисляются по формуле 25. В матрице А найти строку с наибольшей суммой элементов и ее номер. Элементы матрицы А вычисляются по формуле i, j = 1, 2, …, 10. 26. В матрице А найти строку с наименьшей суммой элементов и ее номер. Элементы матрицы А вычисляются по формуле
27. В матрице А найти строку с наименьшим элементом и упорядо- чить элементы этой строки по возрастанию. Результат записать в мат- рицу В. Элементы матрицы А вычисляются по формуле 28. В матрице А найти строку с наибольшим элементом и упорядо- чить элементы этой строки по убыванию. Результат записать в матрицу В. Элементы матрицы А вычисляются по формуле i, j = 1, 2, …, 10. 29. В матрице А найти столбец с наименьшим элементом и упорядо- чить элементы этого столбца по возрастанию. Результат записать в мат- рицу В. Элементы матрицы А вычисляются по формуле i, j = 1, 2, …, 10. 30. В матрице А найти столбец с наибольшим элементом и упорядо- чить элементы этого столбца по убыванию. Результат записать в матри- цу В. Элементы матрицы А вычисляются по формуле i, j = 1, 2, …, 10.
Контрольные вопросы 1. Перечислите способы описания двумерных массивов. 2. Как располагаются в памяти ЭВМ элементы двумерных масси- вов? 3. Как осуществляется ввод и вывод двумерных массивов? 4. Дайте определение массива. 5. Верно ли, что могут существовать массивы массивов?
Лабораторная работа № 6
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 577; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.186.156 (0.008 с.) |

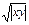 , xÎ [–1; 1], yÎ [–1; 2], n = m = 10. Координаты векто-
ра X равны элементам матрицы В, стоящим на главной диа-
гонали
, xÎ [–1; 1], yÎ [–1; 2], n = m = 10. Координаты векто-
ра X равны элементам матрицы В, стоящим на главной диа-
гонали
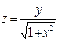 , x Î [0; 1], y Î [0; 1], n = m = 10. Координаты век-
тора X равны разности соответствующих элементов первой и
второй строк матрицы В
, x Î [0; 1], y Î [0; 1], n = m = 10. Координаты век-
тора X равны разности соответствующих элементов первой и
второй строк матрицы В
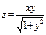 , x Î [0; 1], y Î [0; 1], n = m = 10. Координаты век-
тора X равны произведению соответствующих элементов
первой и второй строк матрицы В
, x Î [0; 1], y Î [0; 1], n = m = 10. Координаты век-
тора X равны произведению соответствующих элементов
первой и второй строк матрицы В
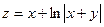 ,x Î [1; 2], y Î [0; 1], n = m = 10. Координаты
вектора X равны модулю суммы соответствующих элементов
первой и второй строк матрицы В
,x Î [1; 2], y Î [0; 1], n = m = 10. Координаты
вектора X равны модулю суммы соответствующих элементов
первой и второй строк матрицы В
 , x Î [0; 1], y Î [0; 1], n = m = 10. Координаты
вектора X равны –1, если соответствующие элементы первой
и второй строк матрицы В отрицательны, в противном случае
координаты равны +1
, x Î [0; 1], y Î [0; 1], n = m = 10. Координаты
вектора X равны –1, если соответствующие элементы первой
и второй строк матрицы В отрицательны, в противном случае
координаты равны +1
 , x Î [0; 1], y Î [0; 1], n = m = 10. Координаты векто-
ра X равны среднему арифметическому соответствующих
координат первых строк матриц А и В
, x Î [0; 1], y Î [0; 1], n = m = 10. Координаты векто-
ра X равны среднему арифметическому соответствующих
координат первых строк матриц А и В
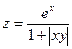 , x Î [0; 1], y Î [0; 1], n = m = 10. Все координаты
вектора X равны среднему арифметическому максимального
и минимального элементов первой строки матрицы В
, x Î [0; 1], y Î [0; 1], n = m = 10. Все координаты
вектора X равны среднему арифметическому максимального
и минимального элементов первой строки матрицы В
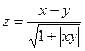 , x Î [0; 1], y Î [0; 1], n = m = 10. Координаты век-
тора X равны 0, если элементы первой строки матрицы В от-
рицательные, в противном случае координаты равны +1.
, x Î [0; 1], y Î [0; 1], n = m = 10. Координаты век-
тора X равны 0, если элементы первой строки матрицы В от-
рицательные, в противном случае координаты равны +1.
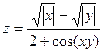 , x Î [0; 1], y Î [0; 1], n = m = 10. Все координа-
ты вектора X равны числу отрицательных элементов в пер-
вой строке матрицы В
, x Î [0; 1], y Î [0; 1], n = m = 10. Все координа-
ты вектора X равны числу отрицательных элементов в пер-
вой строке матрицы В
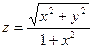 , x Î [0; 1], y Î [0; 1], n = m = 10. Координаты век-
тора X равны соответствующим элементам главной диагона-
ли матрицы B
, x Î [0; 1], y Î [0; 1], n = m = 10. Координаты век-
тора X равны соответствующим элементам главной диагона-
ли матрицы B
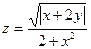 , xÎ[0; 1], yÎ[0; 1], n = m = 10. Координаты векто-
ра X равны сумме соответствующих элементов первой и вто-
рой строк матрицы В
, xÎ[0; 1], yÎ[0; 1], n = m = 10. Координаты векто-
ра X равны сумме соответствующих элементов первой и вто-
рой строк матрицы В
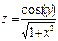 , xÎ[0; 1], yÎ[0; 1], n = m = 10. Все координаты вектора X равны числу положительных элементов в первой строке матрицы В
, xÎ[0; 1], yÎ[0; 1], n = m = 10. Все координаты вектора X равны числу положительных элементов в первой строке матрицы В
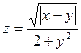 , xÎ[0; 1], yÎ[0; 1], n = m = 10. Координаты вектора X равны разности соответствующих элементов первой и второй строк матрицы В
, xÎ[0; 1], yÎ[0; 1], n = m = 10. Координаты вектора X равны разности соответствующих элементов первой и второй строк матрицы В
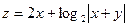 , xÎ[0; 1], yÎ[0; 1], n = m = 10. Координаты
вектора X равны –1, если соответствующие элементы первой
и второй строк матрицы В отрицательны, в противном случае
координаты равны +1
, xÎ[0; 1], yÎ[0; 1], n = m = 10. Координаты
вектора X равны –1, если соответствующие элементы первой
и второй строк матрицы В отрицательны, в противном случае
координаты равны +1
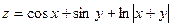 ,xÎ[1; 2], yÎ[0; 1], n = m = 10. Координаты вектора X равны модулю суммы соответствующих элементов первой и второй строк матрицы В
,xÎ[1; 2], yÎ[0; 1], n = m = 10. Координаты вектора X равны модулю суммы соответствующих элементов первой и второй строк матрицы В
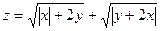 , xÎ [0; 1], yÎ [0; 1], n = m = 10. Все координаты вектора X равны разности между числом положительных и числом отрицательных элементов первой строки матрицы В
, xÎ [0; 1], yÎ [0; 1], n = m = 10. Все координаты вектора X равны разности между числом положительных и числом отрицательных элементов первой строки матрицы В
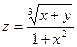 , xÎ [0; 1], yÎ [0; 1], n = m = 10. Координаты век-
тора X равны соответствующим элементам главной диагона-
ли матрицы B
, xÎ [0; 1], yÎ [0; 1], n = m = 10. Координаты век-
тора X равны соответствующим элементам главной диагона-
ли матрицы B
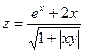 , xÎ [0; 1], yÎ [0; 1], n = m = 10. Координаты век-
тора X равны 0, если элементы первой строки матрицы В от-
рицательные, в противном случае координаты равны +1.
, xÎ [0; 1], yÎ [0; 1], n = m = 10. Координаты век-
тора X равны 0, если элементы первой строки матрицы В от-
рицательные, в противном случае координаты равны +1.
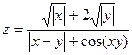 , x Î [0; 1], y Î [0; 1], n = m = 10. Все коорди-
наты вектора X равны среднему арифметическому элементов
второй строки матрицы В
, x Î [0; 1], y Î [0; 1], n = m = 10. Все коорди-
наты вектора X равны среднему арифметическому элементов
второй строки матрицы В
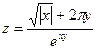 ,, x Î [0; 1], y Î [0; 1], n = m = 10. Все координа-
ты вектора X равны разности между числом положительных
и числом отрицательных элементов первой строки матрицы
В
,, x Î [0; 1], y Î [0; 1], n = m = 10. Все координа-
ты вектора X равны разности между числом положительных
и числом отрицательных элементов первой строки матрицы
В
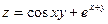 , x Î [0; 1], y Î [0; 1], n = m = 10. Координаты
вектора X равны модулю разности соответствующих элементов
первой и второй строк матрицы В
, x Î [0; 1], y Î [0; 1], n = m = 10. Координаты
вектора X равны модулю разности соответствующих элементов
первой и второй строк матрицы В
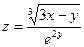 ,, x Î [0; 1], y Î [0; 1], n = m = 10. Координаты векто-
ра X равны среднему арифметическому соответствующих
координат второрых строк матриц А и В
,, x Î [0; 1], y Î [0; 1], n = m = 10. Координаты векто-
ра X равны среднему арифметическому соответствующих
координат второрых строк матриц А и В
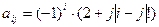 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.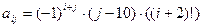 , j где i, j = 1, 2, …, 10.
, j где i, j = 1, 2, …, 10.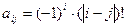 ,где i, j = 1, 2, …, 10.
,где i, j = 1, 2, …, 10.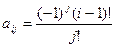 ,где i, j = 1, 2, …, 10.
,где i, j = 1, 2, …, 10.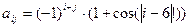 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.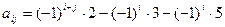 где i, j = 1, 2, …, 10.
где i, j = 1, 2, …, 10.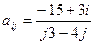 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.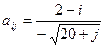 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.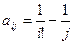 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.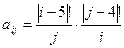 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.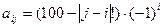 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.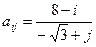 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.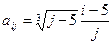 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.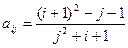 , j где i, j = 1, 2, …, 10.
, j где i, j = 1, 2, …, 10.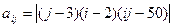 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.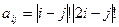 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.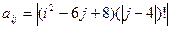 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.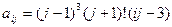 где i, j = 1, 2, …, 10.
где i, j = 1, 2, …, 10.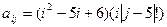 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.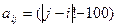 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.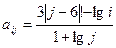 , j где i, j = 1, 2, …, 10.
, j где i, j = 1, 2, …, 10.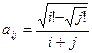 , где
, где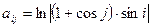 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.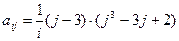 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.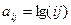 , где
, где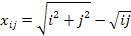 , где i, j = 1, 2, …, 10.
, где i, j = 1, 2, …, 10.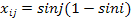 , a j i i j = × - где i, j = 1, 2, …, 10.
, a j i i j = × - где i, j = 1, 2, …, 10.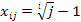 ,где
,где , где
, где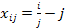 , где
, где


