Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы вычерчивания графических примитивов.Содержание книги
Поиск на нашем сайте
Точка: Поверхности, на которую программа может осуществлять вывод графики, соответствует объект Canvas. Свойство pixels, представляющее собой двумерный массив типа TColor, содержит информацию о цвете каждой точки графической поверхности. Используя свойство Pixels, можно задать требуемый цвет для любой точки графической поверхности, т. е. "нарисовать" точку. Например, инструкция Form1.Canvas.Pixels[10,10]:=clRed окрашивает точку поверхности формы в красный цвет. Прямая линия: Вычерчивание прямой линии осуществляет метод LinеТо, инструкция вызова которого в общем виде выглядит следующим образом: Компонент.Canvas.LineTo(x,у) Метод LinеТо вычерчивает прямую линию от текущей позиции карандаша в точку с координатами, указанными при вызове метода. Окружность и эллипс: Метод Ellipse вычерчивает эллипс или окружность, в зависимости от значений параметров. Инструкция вызова метода в общем виде выглядит следующим образом: Объект.Canvas.Ellipse(x1,y1, х2,у2] где: объект — имя объекта (компонента), на поверхности которого выполняется вычерчивание; x1, y1, х2, у2 — координаты прямоугольника, внутри которого вычерчивается эллипс или, если прямоугольник является квадратом, окружность. Дуга: Вычерчивание дуги выполняет метод Arc, инструкция вызова которого в общем виде выглядит следующим образом:
Объект.Canvas.Arc(x1,y1,х2,у2,х3,у3,х4,у4)
где: x1, y1, х2, у2 — параметры, определяющие эллипс (окружность), частью которого является вычерчиваемая дуга; х3, у3 — параметры, определяющие начальную точку дуги; П х4, у4 — параметры, определяющие конечную точку дуги. Прямоугольник Прямоугольник вычерчивается методом Rectangle, инструкция вызова которого в общем виде выглядит следующим образом: Объект.Canvas.Rectangle(x1, y1,x2, y2) где: объект — имя объекта (компонента), на поверхности которого выполняется вычерчивание; x1, y1 и х2, у2 — координаты левого верхнего и правого нижнего углов прямоугольника. Метод RoundRec тоже вычерчивает прямоугольник, но со скругленными углами. Инструкция вызова метода RoundRec выглядит так: Объект.Canvas.RoundRec(x1,y1,х2, у2, х3, у3) где: x1, y1, х2, у2 -- параметры, определяющие положение углов прямоугольника, в который вписывается прямоугольник со скругленными углами; х3 и у3 — размер эллипса, одна четверть которого используется для вычерчивания скругленного угла. Сектор: Метод pie вычерчивает сектор эллипса или круга. Инструкция вызова метода в общем виде выглядит следующим образом: Объект. Canvas.Pie(x1,y1,x2,y2,х3,у3,х4,у4) где: x1, y1, х2, у2 — параметры, определяющие эллипс (окружность), частью которого является сектор; х3, у3, х4, у4 — параметры, определяющие координаты конечных точек прямых, являющихся границами сектора. Начальные точки прямых совпадают с центром эллипса (окружности). Сектор вырезается против часовой стрелки от прямой, заданной точкой с координатами (хЗ, уз), к прямой, заданной точкой с координатами (х4, у4) Задание к выполнению лабораторной работы Задание А Выполнить пример, приведенный в описании порядка выполнения данной лабораторной работы. Задание Б Выбрать алгоритм, составить блок-схему и программу для вычисления в точках xi = a + i×h, i = 0,1,2…, n, h = (b – a)/n промежутка [ a,b ] наибольшего и среднего значений функции y = f(x), указанной в варианте задания. Для выполнения задания воспользоваться оператором цикла FOR; Задание В Выбрать алгоритм, составить блок-схему и программу для реше- ния заданной задачи в выбранном варианте задания. При решении зада- чи использовать операторы цикла WHILE и REPEAT. Для решения первой и второй задач выбранного варианта преду- смотреть: 1) ввод в программу параметров с клавиатуры; 2) вывод на экран значений параметров и вычисляемых величин.
Задание Г Разработать алгоритм, составить его блок-схему и программу для решения задачи, указанной в соответствующем варианте. Подобрать тестовые данные и протестировать. Порядок выполнения работы
Пример1. Использования оператора цикла while Вычислить сумму членов бесконечного ряда с заданной точностью e =10-4 при x =5.
Прежде всего находят ОДЗ переменной, Х>0. Открыть новое приложение с помощью команды File| New Application. Сохранить проект. 1. На форме Form1 разместить компоненты Label1, Label2, Labe3; Memo1; Edit1, Button1, Button2 как показано на рис. 3.1. 2. Свойству Caption метки Label1 задать значение ’Введите значение переменной Х’ 3. Текст выровнять по центру, установив следующие значения свойств: AutoSize – False WordWrap – True Alignment – taCenter Размеры метки и ее местоположение отрегулировать вручную. Размер и тип шрифта установить с помощью свойства Font. 4. Свойству Caption метки Label3 задать значение ’ Вычисление суммы членов бесконечного ряда с заданной точностью =10-4 при различных x’
5. Для метки Label2 установить свойство Caption равным ‘X=’. 6. Для компонента Edit1 установить свойство Text равным пустой строке. 7. Для компонента Memo1 выбрать свойство Lines и открыть окно String list editor. Удалить в нем строку ‘Memo1’. 8. Для кнопок Button1, Button2 установить свойство Caption равным ‘Решение’ и ’Очистить’ соответственно. 9. Выполнить двойной щелчок на кнопке ‘Решение’ и определить следующий обработчик события OnClick: procedure TForm1.Button1Click(Sender: TObject); var s, eps, x, un, uk, y:real; i:integer; begin x:=StrToFloat(Edit1.Text); if x<=0 then begin Memo1.Lines.Add('Значение X не входит в ОДЗ'); exit; end; eps:=1e-5; s:=1; i:=1; y:=-1*2; un:=(ln(x)/ln(10))/y; while abs(un)>eps Do begin s:=s+un; uk:=un; i:=i+1; y:=-y*(2*i-1)*(2*i); un:=ln(i*x)/ln(10)/y; end; Memo1.Lines.Add('Результат'); Memo1.Lines.Add('s='+FloatToStr(s)); Memo1.Lines.Add('n='+FloatToStr(i)); Memo1.Lines.Add('u='+FloatToStr(uk));
end;
Рис. 3.3. Вид приложения
10. Вернуться в форму с помощью клавиши F12, выполнить двойной щелчок на кнопке ‘Очистить’ и определить следующий обработчик события OnClick: procedure TForm1.Button2Click(Sender:TObject); begin Memo1.Clear; end; 11. Откомпилировать и выполнить программу. Результат работы программы показан на Рис. 3.4
Рис. 3.4. Результат работы программы.
Пример2. Создание простейшего изображения. 1. Открыть новое приложение с помощью команды File|New Application. Сохраните проект в вашем рабочем каталоге, выполнив команду меню File|Save Project As. 2. Запустить графический редактор командой Tools|Image Editor. 3. В графическом редакторе выполнить команду File|New|Bitmap File (.bmp). 4. В появившемся диалоговом окне Bitmap Properties установить Width=300 Height=200 Colors=SuperVGA(256 colors) 5. Создать произвольное изображение, пример которого приведен на рис.3.5.
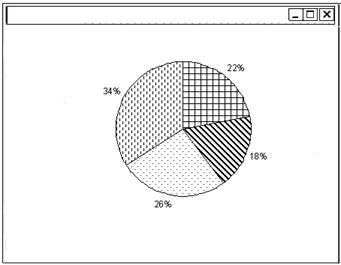
Рис.3.5. Пример изображения Для того чтобы выбрать цвет символов, следует подвести курсор мыши к окну с требуемым цветом в палитре цветов и нажать левую клавишу. При нажатой правой клавише мыши выбранный цвет будет использоваться в качестве цвета фона. После выбора цвета для символов и фона следует выполнить команды Edit|Select All и Edit|Cut для очистки рисунка. После этого вставить приведенный выше текст. 6. Выполнить команду File|Save и сохранить изображение в файле с именем zast.bmp. 7. Поместить на форму компонент TImage (страница Additional). 8. Выбрать свойство Picture и войти в редактор свойств (кнопка с тремя точками). 9. В появившемся окне Picture Editor нажать кнопку Load и выбрать файл zast.bmp. 10. Установить свойство AutoSize компонента TImage в True. 11. Поместить на форму компонент TTimer (страница System) и установит свойство Interval равным 1000. 12. Активизировать компонент Timer1 двойным щелчком и создать следующий обработчик события OnTimer. procedure TForm1.Timer1Timer(Sender: TObject); begin if Image1.Visible=True then begin Timer1.Interval:=8000; Image1.Hide; end else begin Timer1.Interval:=2000; Image1.Show; end; end; 13. Запустить проект на выполнение. Пример 3. Создание приложения, содержащего круговую диаграмму. 1. Открыть новое приложение. 2. Поместить на форму компонент TPaintBox (страница System) и установить его размеры: Height – 250, Width – 250. 3. В Инспекторе объектов перейти на вкладку Events и дважды щелкнуть по правому полю в строке события OnPaint. 4. Записать следующий обработчик события: procedure TForm1.PaintBox1Paint(Sender: TObject); begin sector(clRed,0,pi/3,'16,5%'); sector(clWhite,pi/3,5*pi/6,'25%'); sector(clBlue,5*pi/6,7*pi/5,'28,4%'); sector(clYellow,7*pi/5,2*pi,'30%'); end; Для рисования сектора круга в этом обработчике определена функция sector с параметрами: Cls – цвет, которым закрашивается сектор; angle1 – начальный угол; angle2 – конечный угол; msg – текст в секторе.
Рис. 3.6. Результат работы приложения Эту функцию надо добавить перед обработчиком события: procedure sector(clr:TColor;angle1,angle2:real;msg:string); Var x1,x2,y1,y2:integer; begin PaintBox1.Canvas.Brush.Color:=clr; x1:=trunc(cos(angle1)*PaintBox1.Width/2+PaintBox1.Width/2); y1:=PaintBox1.Height-trunc(sin(angle1)*PaintBox1.Height/2+PaintBox1.Height/2); x2:=trunc(cos(angle2)*PaintBox1.Width/2+PaintBox1.Width/2); y2:=PaintBox1.Height-trunc(sin(angle2)*PaintBox1.Height/2+PaintBox1.Height/2); PaintBox1.Canvas.Pie(0,0,PaintBox1.Width, PaintBox1.Height,x1,y1,x2,y2); PaintBox1.Font.Name:='Arial'; PaintBox1.Font.Size:=8; PaintBox1.Font.Color:=clBlack; PaintBox1.Font.Style:=[fsBold]; PaintBox1.Canvas.TextOut(trunc((x1+x2)/2-20),trunc((y1+y2)/2),msg); end; 5. Откомпилировать и выполнить приложение.
Содержание отчета 6. Тема, цель лабораторной работы и постановка задания в соответствии с вариантом. 7. Схематичное изображение главной формы приложения для заданий Б и В. 8. Блок-схемы. 9. Тексты программ. 10. Ответы на контрольные вопросы. Варианты заданий Задание Б
Задание В 1. Пользуясь тем, что
вычислить значение sin(x) для указанного значения Замечание. Если 2. Используя представление
вычислить значение p с точностью e = 0,0001. Замечание. Если n - номер слагаемого в (3.2), то его значение ределяется по формуле выполненной, если 3. Используя представление
вычислить значение e = 0,001. Замечание. Очередной член предыдущий член Если в (3.3) | x | > 1, то полагая x = [ x ] + x, где [ x ] – целая часть x, нужно воспользоваться формулой 4. Найти число M натуральных чисел N – заданное натуральное число. 5. Найти число M натуральных чисел так, чтобы выполнялось условие S £ N, где N – заданное натуральное число. 6. Найти число M натуральных чисел и вычислить сумму N – натуральное число. 7. Найти число M натуральных чисел и вычислить сумму N – натуральное число. 8. Пользуясь тем, что
вычислить значение cos x для указанного значения Замечание. Воспользоваться тем, что отношение последующего чле- на в (3.4) к предыдущему равно 9. Пользуясь тем, что
вычислить значение e с точностью e = 0,0001. Точность вычисления считается выполненной, если последний член в сумме (3.5) меньше e/3. 10. Для числовой последовательности 11. Для числовой последовательности найти первый член и его номер M такой, чтобы 12. Для числовой последовательности первый член и его номер M такой, чтобы
13. Для числовой последовательности 14. Найти наименьшее натуральное число М, кратное 5, для которого
15. Найти наименьшее натуральное число М, кратное 3, для которого
16. Найти наименьшее натуральное число М, кратное 4, для которого
17. Найти наименьшее натуральное число М, кратное 6, для которого
18. Найти наименьшее натуральное число М такое, для которого
19. Найти наименьшее натуральное число М такое, для которого
20. Найти наименьшее натуральное число М такое, для которого
Замечание. Воспользоваться содержанием варианта 8.
21. Найти наименьшее натуральное число М такое, для которого
Замечание. Воспользоваться содержанием варианта 1. 22. Для указанного значения x0 найти наименьшее натуральное чис- ло М такое, что 23. Пользуясь тем, что
при x Î[–1; 1] вычислить значение ln(1 + x) для указанного значения
полненной, если последний по модулю член в сумме (3.6) меньше e. 24. Найти корень e = 0,001, пользуясь формулой 25. Найти корень пользуясь формулой 26. Найти корень 27. Найти корень пользуясь формулой где n = 0,1,…, m = 1/3, 28. Найти корень e = 0,00001. Замечание. Воспользоваться формулой (3.7), где положить m = 1/5;
29. Найти наименьшее натуральное число M такое, для которого
30. Для заданного значения ние М такое, что Варианты заданий
Контрольные вопросы 1. Как называются программы, в основе которых лежит структура повторения? 2. Сколько операторов цикла вам известно? 3. Каков тип выражения в операторе цикла с предусловием? 4. Верно ли, что в теле цикла с предусловием должен находиться один оператор? 5. Как сделать, чтобы в теле цикла было несколько операторов? 6. Когда проверяется истинность выражения в цикле while? 7. Верно ли, что истинность выражения в цикле с предусловием яв- ляется условием продолжения цикла? 8. Сколько раз выполнится оператор в теле цикла while, если с са- мого начала значение выражения равно false? 9. Верно ли, что цикл while используется при вычислении всякого рода сумм и произведений, когда заранее не известно число повторе- ний? 10. Сколько операторов можно записать между ключевыми словами repeat и until? 11. Когда проверяется истинность выражения в операторе цикла repeat? 12. Какой тип имеет выражение в операторе цикла с постусловием? 13. Почему в цикле repeat оператор тела цикла всегда будет выпол- нен хотя бы один раз? 14. Верно ли, что истинность выражения в цикле repeat является ус- ловием окончания цикла? 15. С помощью каких служебных слов записывается цикл с парамет- ром? 16. Верно ли, что цикл с параметром применяется в тех случаях, ко- гда заранее известно число повторений? 17. Пусть цикл записан в виде: for v:=El to Е2 do S; а) как называется El? б) как называется Е2? в) как называется v? 18. Может ли вещественная переменная быть параметром цикла for? 19. Какие циклы называются вложенными? 20. С помощью какого компонента можно рисовать на форме? 21.С помощью какого метода можно нарисовать окружность, квадрат, прямоугольник, эллипс?
Лабораторная работа № 4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.184 (0.009 с.) |





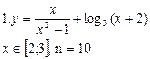

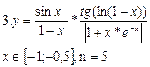
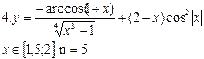

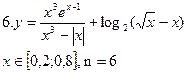
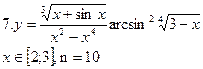


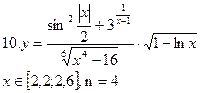


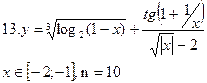
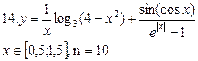

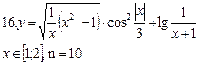
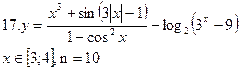
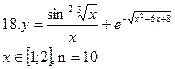


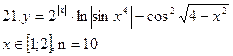
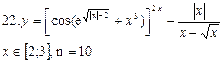

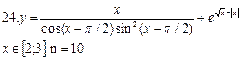
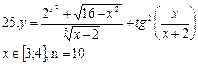
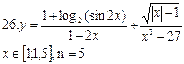
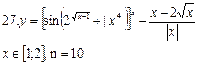
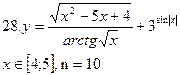

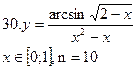
 (3.1)
(3.1) , заданного в радианах, с точностью e = 0,001. Точность вычисления считается выполненной, если последнее слагаемое в (3.1) удовлетворяет условию
, заданного в радианах, с точностью e = 0,001. Точность вычисления считается выполненной, если последнее слагаемое в (3.1) удовлетворяет условию 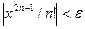 |.
|. - значение k -го слагаемого в (3.1), причем
- значение k -го слагаемого в (3.1), причем  , то
, то 
 (3.2)
(3.2)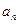 оп-
оп- . Точность вычисления считается
. Точность вычисления считается .
.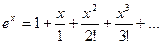 (3.3)
(3.3) для указанного значения
для указанного значения  в сумме (3) выражается через
в сумме (3) выражается через , n = 1,2, … по следующей формуле
, n = 1,2, … по следующей формуле 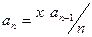 .
.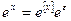 . Точность вычисления считается выполненной, если
. Точность вычисления считается выполненной, если  .
. таких, что
таких, что 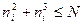 , где
, где

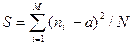 , где N, а – заданные числа;
, где N, а – заданные числа;
 , где N, а – заданные числа,
, где N, а – заданные числа,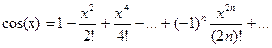 (3.4)
(3.4) .
. (3.5)
(3.5)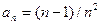 , n = 1,2, … найти первый член и его номер M такой, чтобы
, n = 1,2, … найти первый член и его номер M такой, чтобы 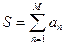 .
.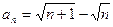 , n = 1,2,…
, n = 1,2,…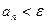 , где e – заданное число, например, e = 0,001 и вычислить сумму
, где e – заданное число, например, e = 0,001 и вычислить сумму 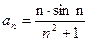 , n = 1,2,… найти
, n = 1,2,… найти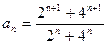 , n = 1,2,… найти первый член и его номер M такой, чтобы
, n = 1,2,… найти первый член и его номер M такой, чтобы 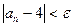 , где e – заданноечисло, например, e = 0,01 и вычислить сумму
, где e – заданноечисло, например, e = 0,01 и вычислить сумму 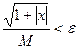 , где e = 0,01, x – заданное число и вычислить сумму
, где e = 0,01, x – заданное число и вычислить сумму  .
.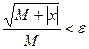 , где e = 0,01, x – заданное число и вычислить сумму
, где e = 0,01, x – заданное число и вычислить сумму .
. , где e = 0,01, x – заданное число и вычислить сумму
, где e = 0,01, x – заданное число и вычислить сумму  .
. , где e = 0,01, x – заданное число и вычислить сумму
, где e = 0,01, x – заданное число и вычислить сумму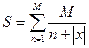 .
.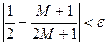 , где e = 0,01 и вычислить сумму
, где e = 0,01 и вычислить сумму 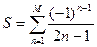 .
.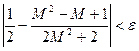 , где e = 0,01 и вычислить сумму
, где e = 0,01 и вычислить сумму  .
. , где e = 0,01, x = 1/M и вычислить сумму
, где e = 0,01, x = 1/M и вычислить сумму  .
. , где e = 0,01, x = 1/M и вычислить сумму
, где e = 0,01, x = 1/M и вычислить сумму 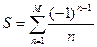 .
. , где e = 0,01 и вычислить сумму
, где e = 0,01 и вычислить сумму 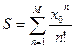 .
. (3.6)
(3.6)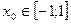 с точностью e = 0,001. Точность вычисления считается вы-
с точностью e = 0,001. Точность вычисления считается вы- уравнения
уравнения 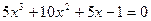 с точностью
с точностью , где n = 0,1,…,
, где n = 0,1,…,  . Точность вычисления считается достигнутой, если
. Точность вычисления считается достигнутой, если 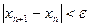 и тогда полагают
и тогда полагают 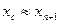 .
. с точностью e = 0,001,
с точностью e = 0,001,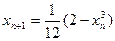 , где n = 0,1,…,
, где n = 0,1,…, 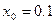 . Точность вычисления считается достигнутой, если
. Точность вычисления считается достигнутой, если  с точностью e = 0,001, пользуясь формулой
с точностью e = 0,001, пользуясь формулой  , где n = 0,1,…,
, где n = 0,1,…,  . Точность вычисления считается достигнутой, если
. Точность вычисления считается достигнутой, если  с точностью e = 0,001,
с точностью e = 0,001,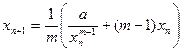 (3.7)
(3.7)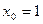 , а = 2. Точность вычисления считается достигнутой, если
, а = 2. Точность вычисления считается достигнутой, если 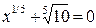 с точностью
с точностью ; а = 10.
; а = 10.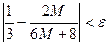 , где e = 0,01 и вычислить
, где e = 0,01 и вычислить  , где e = 0,01, x = 1/M и вычислить сумму
, где e = 0,01, x = 1/M и вычислить сумму  .
.