
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения первого порядка (общие понятия)Стр 1 из 6Следующая ⇒
Уравнения с разделенными и разделяющимися переменными 1. Дифференциальное уравнение вида р (x) dx + q (y) dy = 0(5) называют уравнением с разделенными переменными. Предположим, что функции p (x)и q (y) непрерывны на интервалах (a, b) и (c, d) соответственно. Таким образом, областью D, в которой рассматривается д. у. является прямоугольник (a, b) Если Р (х) и Q (у) – первообразные для p (x)и q (y), то левая часть уравнения (5) является полным дифференциалом функции u (x, y) = Р (х) + Q (у), а само уравнение (5) принимает вид du (x, y) = 0, откуда u (x, y) = С, или Р (х) + Q (у)= С. (6) Выражение (6) есть общий интеграл д.у (5). 2. Уравнение вида М1 (х) N1 (у) dx + М2 (х) N2 (y) dy = 0 (7) называется уравнением с разделяющимися переменными. Предполагаем, что функции М1 (х) и М2 (х) непрерывны на (a, b), а N1 (у)и N2 (y) на (c, d). Если N1 (у 0) = 0, то у = у 0 удовлетворяет уравнению (7). Аналогично, если М2 (х 0) = 0, то х = х 0 также удовлетворяет уравнению (7). Таким образом, (7) имеет решениями функции, графики которых являются частями горизонтальных и вертикальных прямых. Естественно считаем, что х 0 Для точек прямоугольника (a, b)
являющемуся уравнением с разделенными переменными.
Однородные уравнения первого порядка Определение 1. Функция f (x, у)называется однородной функцией п-го измерения относительно переменных х и у, если при любом λ справедливо тождество
Пример 1. Функция f (x, у)=
Пример 2. f (x, у)= Если f (x, у) однородная нулевого измерения, то ее можно представить в виде f (x, у)= т.е. на самом деле f (x, у) является функцией отношения Определение. Уравнение первого порядка
называется однородным относительно х и у,если функция Заменой
(9) сводится к уравнению с разделяющимися переменными. Действительно, по (10) и (8)
откуда
Если
- решение (9). Для
Если Ф (и) - первообразная для
- общий интеграл д.у. (9). Уравнение Бернулли Рассмотрим уравнение вида
где Р (х)и Q (х) — непрерывные на некотором интервале (а, b) (или постоянные), а Разделив все члены уравнения на уп, получим:
Сделаем, далее, замену: z=y-n+ 1. Тогда
Подставляя эти значения в уравнение (26), будем иметь линейное уравнение
Найдя его общий интеграл и подставив вместо z выражение у-п+ 1,получим общий интеграл уравнения Бернулли. Пример. Решить уравнение ○ Так как
Далее полученное уравнение Бернулли решаем с помощью подстановки Полагаем Для определения и имеем уравнение Замечание. Аналогично тому, как это делалось для линейных уравнений, можно показать, что решение уравнения Бернулли можно искать в виде произведения двух функций: y = u (x) v (x), где v (x) — какая-либо функция, отличная от нуля и удовлетворяющая уравнению v'+Pv = 0. Задание. Решите предыдущий пример методом Бернулли. II. Уравнение вида
не содержит явным образом искомой функции у. Порядок такого уравнения можно понизить, взяв за новую неизвестную функцию низшую из производных данного уравнения, т.е. полагая
Таким образом, порядок уравнения понизился на k единиц. Уравнение второго порядка, разрешенное относительно наивысшей производной, данного вида имеет вид
Рассмотрим его решение. Обозначим производную
относительно неизвестной функции z от х. Проинтегрировав это уравнение, находим его общее решение:
а затем из соотношения
Пример. Найти общее решение уравнения ○ Полагаем
Это однородное уравнение первого порядка. Полагая
В полученном уравнении разделяем переменные и интегрируем:
Т.к.
III. Уравнение вида
Линейные однородные уравнения. Определения и общие свойства Определение. Дифференциальное уравнение п -го порядка называется линейным, если оно первой степени относительно искомой функции у и ее производных у ',..., у (п -1), у (п) т. е. имеет вид
где а 0, a 1, a 2, ...,ап и f (x) — заданные функции от х или постоянные, причем Установим некоторые основные свойства линейных однородных уравнений, ограничиваясь в доказательствах уравнениями второго порядка. Теорема 1. Если у 1и у 2— два частных решения линейного однородного уравнения второго порядка
то функция
— линейная комбинация решений у 1и у 2также решение этого уравнения. Доказательство. Так как у 1и у 2— решения уравнения, то
Подставляя в уравнение (44) сумму
т.е. Определение. Два решения уравнения (44) у 1и у 2называются линейно независимыми на отрезке
В противном случае решения называются линейно зависимыми. Иными словами, два решения у 1и у 2называются линейно зависимыми на отрезке Определение. Если у 1и у 2суть функции от х,то определитель
называется определителем Вронского или вронскианом данных Теорема 2. Если функции у 1и у 2линейно зависимы на отрезке Действительно, если
Теорема 3. Если решения у 1и у 2уравнения (44) линейно независимы на отрезке Теорема 4. Если у 1и у 2— два линейно независимых на отрезке
есть его общее решение. Доказательство. Из теоремы 1 следует, что функция Докажем теперь, что каковы бы ни были начальные условия Так как
Равенства (47) представляют собой систему линейных алгебраических уравнений с неизвестными С 1и С 2 . Определитель этой системы
есть определитель Вронского при х = х 0и, следовательно, не равен 0 (в силу линейной независимости решений у 1и у 2). С 1и С 2 найдем применяя, например, формулы Крамера. Частное решение, которое получится из семейства (45) при найденных значениях С 1и С 2 , удовлетворяет заданным начальным условиям. Таким образом, теорема доказана.
Замечание. Не существует общих методов для нахождения в конечном виде общего решения линейного уравнения с переменными коэффициентами. Однако для уравнения с постоянными коэффициентами такой метод существует. Он будет изложен в следующем пункте.
Коэффициентами Рассмотрим линейное однородное уравнение п -го порядка:
Будем предполагать, что а 1, а 2,..., ап — постоянные. Прежде чем указывать метод решения уравнения (54), введем определение, нужное нам для дальнейшего. Определение. Если для всех х отрезка
где A 1, А 2,..., Ап — постоянные числа, не все равные нулю, то говорят, что Определение. п функций Замечание 1. Из определений следует, что если функции
Пример. Функции
не будет тождественно равно нулю. Перейдем теперь к решению уравнения (54). Для этого уравнения справедлива следующая теорема. Теорема. Если функции у = С 1 у 1 + С 2 у 2+....+ Спуп (55) где С 1,..., Сп — произвольные постоянные. Если коэффициенты уравнения (54) постоянны, то общее решение находится так же, как и в случае уравнения второго порядка. 1) Составляем характеристическое уравнение
2) Находим корни характеристического уравнения 3) По характеру корней выписываем частные линейно независимые решения, руководствуясь тем, что: а) каждому действительному однократному корню k соответствует частное решение еkх; б) каждой паре комплексных сопряженных однократных корней в) каждому действительному корню k кратности r соответствует r линейно независимых частных решений
г) каждой паре комплексных сопряженных корней кратности s соответствуют 2 s частных решений:
Этих частных решений будет ровно столько, какова степень характеристического уравнения (т. е. столько, каков порядок данного линейного дифференциального уравнения). Можно доказать, что эти решения линейно независимы.
4) Найдя п линейно независимых частных решений y 1, y 2,..., уп, строим общее решение данного линейного уравнения:
Пример. Найти общее решение уравнения ○ Составляем характеристическое уравнение Находим корни характеристического уравнения:
Записываем общее решение:
Дифференциальные уравнения первого порядка (общие понятия) Дифференциальное уравнение первого порядка имеет вид
Если это уравнение можно разрешить относительно
В этом случае мы говорим, что дифференциальное уравнение разрешено относительно производной. Для такого уравнения справедлива следующая теорема, которая называется теоремой о существовании и единственности решения дифференциального уравнения. Теорема. Если в уравнении Геометрический смысл теоремы заключается в том, что существует и притом единственная функция Условие, что при х = х 0функция у должна равняться заданному числу у 0,называется начальным условием. Определение. Общим решением дифференциального уравнения первого порядка называется функция
которая зависит от одного произвольного постоянного С и удовлетворяет следующим условиям: а) она удовлетворяет дифференциальному уравнению при любом б) каково бы ни было начальное условие В процессе разыскания общего решения дифференциального уравнения мы нередко приходим к соотношению вида Ф (х, у,С) = 0, (2') не разрешенному относительно у. Разрешив это соотношение относительно у,получаем общее решение. Однако выразить у из соотношения (2') в элементарных функциях не всегда оказывается возможным; в таких случаях общее решение оставляется в неявном виде. Равенство Ф (х, у,С) = 0 называется общим интегралом дифференциального уравнения. Определение. Частным решением называется любая функция Пример. Для уравнения первого порядка
общим решением будет семейство функций у = Найдем частное решение, удовлетворяющее следующему начальному условию: у 0 = 1 при х 0 = 2. Подставляя эти значения х 0и у 0в формулу у =
Геометрически общий интеграл представляет собой семейство кривых на координатной плоскости, зависящее от одной произвольной постоянной С (или, как говорят, от одного параметра С). Эти кривые называются интегральными кривыми данного дифференциального уравнения. Частному интегралу соответствует одна кривая этого семейства, проходящая через некоторую заданную точку (х 0, у 0) плоскости. Так, в последнем примере общий интеграл геометрически изображается семейством гипербол у = Замечание. Уравнение Дадим геометрическую интерпретацию дифференциального уравнения первого порядка. Пусть дано дифференциальное уравнение, разрешенное относительно производной:
и пусть Уравнение (1') для каждой точки М с координатами х и у определяет знание производной Следовательно, с геометрической точки зрения задача интегрирования дифференциального уравнения заключается в нахождении кривых, направление касательных к которым совпадает с направлением поля в соответствующих точках. Для дифференциального уравнения (1) геометрическое место точек, в которых выполняется соотношение
На рис. 2 изображено поле направлений, определяемое дифференциальным уравнением Изоклинами данного дифференциального уравнения является семейство прямых у = - Сх. Эти прямые изображены на рис. 2. Рассмотрим такую задачу: Пусть дано семейство функций, зависящее от одного параметра С:
причем через каждую точку области D на плоскости проходит только одна кривая из этого семейства. Для какого дифференциального уравнения это семейство функций является общим интегралом? Из соотношения (3), дифференцируя по х, найдем:
Так как через каждую точку области D проходит только одна кривая семейства, то для каждой пары чисел х и у определяется единственное значение С из уравнения (3). Подставляя это значение С в соотношение (4), найдем Следовательно, чтобы написать дифференциальное уравнение, общий интеграл которого определяется формулой (3), нужно исключить С из соотношений (3) и (4).
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.13.255 (0.116 с.) |
 (c, d) на плоскости хОу.
(c, d) на плоскости хОу. (a, b), а у 0
(a, b), а у 0  ,
, .
.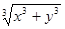 - однородная функция первого измерения, так как
- однородная функция первого измерения, так как .
.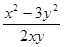 есть однородная функция нулевого измерения, т.к
есть однородная функция нулевого измерения, т.к  , т.е.
, т.е. 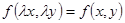 .
. (8)
(8)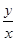 .
.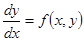 (9)
(9)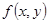 есть однородная функция нулевого измерения относительно х и у.
есть однородная функция нулевого измерения относительно х и у.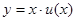 (10)
(10)
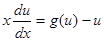 . (11)
. (11)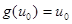 , то
, то 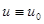 - решения (11), так что
- решения (11), так что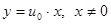 (12)
(12)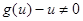 и
и  уравнение (11) равносильно
уравнение (11) равносильно (13)
(13)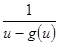 , то
, то 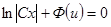 - общий интеграл д.у. (13), а
- общий интеграл д.у. (13), а (14)
(14)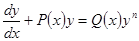 (25)
(25)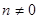 и
и 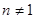 (в противном случае получилось бы линейное уравнение или д. у. с разделяющимися переменными). Это уравнение, называемое уравнением. Бернулли,приводится к линейному следующим преобразованием.
(в противном случае получилось бы линейное уравнение или д. у. с разделяющимися переменными). Это уравнение, называемое уравнением. Бернулли,приводится к линейному следующим преобразованием.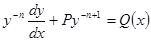 (26)
(26)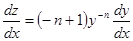 .
.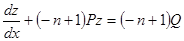 . (27)
. (27)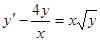
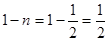 , то воспользовавшись (27) имеем:
, то воспользовавшись (27) имеем: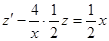 .
. . Имеем
. Имеем 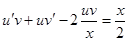 или
или 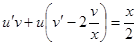 .
. откуда
откуда  ; интегрируя, находим
; интегрируя, находим  , или
, или 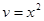 (постоянную интегрирования не вводим, так как достаточно найти какое – либо частное решение этого вспомогательного уравнения).
(постоянную интегрирования не вводим, так как достаточно найти какое – либо частное решение этого вспомогательного уравнения).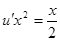 или
или 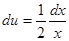 , откуда находим
, откуда находим  . Тогда
. Тогда  , т.к.
, т.к.  , то
, то 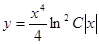 .●
.●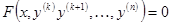 , (36)
, (36)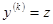 . Тогда получим уравнение
. Тогда получим уравнение .
.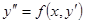 . (37)
. (37)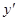 через z, тогда
через z, тогда 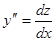 . Подставляя эти выражения производных в уравнение (37), получим уравнение первого порядка
. Подставляя эти выражения производных в уравнение (37), получим уравнение первого порядка
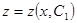 ,
,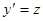 получаем общий интеграл уравнения (37):
получаем общий интеграл уравнения (37):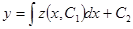 .
.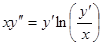 .
. , преобразуем уравнение к виду
, преобразуем уравнение к виду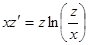 или
или 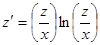 .
.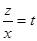 , откуда
, откуда  , получим уравнение
, получим уравнение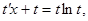
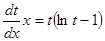 .
.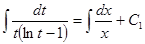 .
.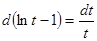 , то имеем
, то имеем 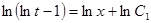 , или
, или  , откуда
, откуда 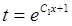 . Следовательно,
. Следовательно, (выше был использован метод интегрирования «по частям»).
(выше был использован метод интегрирования «по частям»).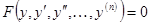 , (38)
, (38)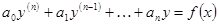 , (43)
, (43) для всех значений х из той области, в которой мы рассматриваем уравнение (43). В дальнейшем мы будем предполагать, что функции а 0, a 1, a 2, ...,ап и f (x) непрерывны на некотором интервале
для всех значений х из той области, в которой мы рассматриваем уравнение (43). В дальнейшем мы будем предполагать, что функции а 0, a 1, a 2, ...,ап и f (x) непрерывны на некотором интервале 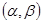 оси х,причем коэффициент а 0 = 1 (если он не равен 1, мы можем все члены уравнения поделить на него). Функция f (x), стоящая в правой части уравнения, называется правой частью уравнения. Если
оси х,причем коэффициент а 0 = 1 (если он не равен 1, мы можем все члены уравнения поделить на него). Функция f (x), стоящая в правой части уравнения, называется правой частью уравнения. Если  , то уравнение называется линейным однородным, в противном случае — линейным неоднородным.
, то уравнение называется линейным однородным, в противном случае — линейным неоднородным.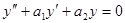 , (44)
, (44)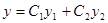 (45)
(45)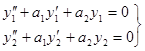 (46)
(46)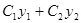 и принимая во внимание тождества (46), будем иметь:
и принимая во внимание тождества (46), будем иметь:
 , если их отношение на этом отрезке не является постоянным, т. е. если
, если их отношение на этом отрезке не является постоянным, т. е. если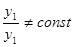 .
.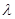 , что
, что 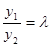 при
при  . В этом случае
. В этом случае  .
.
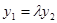 где
где  , то
, то 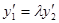 и
и .
.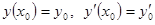 , где
, где 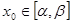 можно так подобрать значения произвольных постоянных С 1и С 2, чтобы соответствующее частное решение
можно так подобрать значения произвольных постоянных С 1и С 2, чтобы соответствующее частное решение  , то подставляя начальные условия, будем иметь:
, то подставляя начальные условия, будем иметь: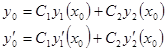 (47)
(47)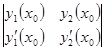
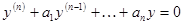 . (54)
. (54) ,
,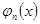 выражается линейно через функции
выражается линейно через функции  .
. называются линейно независимыми, если никакая из этих функций линейно не выражается через остальные.
называются линейно независимыми, если никакая из этих функций линейно не выражается через остальные.
 линейно независимы, так как ни при каких С 1, С 2, С 3, одновременно не равных нулю, выражение
линейно независимы, так как ни при каких С 1, С 2, С 3, одновременно не равных нулю, выражение
 являются линейно независимыми решениями уравнения (54), то его общее решение есть
являются линейно независимыми решениями уравнения (54), то его общее решение есть .
. .
. соответствуют два частных решения
соответствуют два частных решения  и
и  ;
; ;
;
 .
. .
.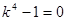 .
. .
. .
.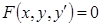 . (1)
. (1)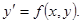 (1')
(1')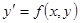 функция
функция 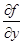 по у непрерывны в некоторой области D на плоскости Оху, содержащей некоторую точку (х 0, у 0), то существует единственное решение этого уравнения
по у непрерывны в некоторой области D на плоскости Оху, содержащей некоторую точку (х 0, у 0), то существует единственное решение этого уравнения  , удовлетворяющее условию
, удовлетворяющее условию 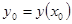 .
.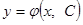 (2)
(2)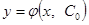 удовлетворяет данному начальному условию. При этом точка (х 0, у 0)
удовлетворяет данному начальному условию. При этом точка (х 0, у 0)  , где D - область изменения переменных х и у, в которой выполняются условия теоремы существования и единственности решения.
, где D - область изменения переменных х и у, в которой выполняются условия теоремы существования и единственности решения.
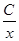 ; это можно проверить подстановкой в уравнение.
; это можно проверить подстановкой в уравнение. , т. е. угловой коэффициент касательной к интегральной кривой, проходящей через эту точку. Таким образом, дифференциальное уравнение (1') определяет поле направлений на плоскости Оху.
, т. е. угловой коэффициент касательной к интегральной кривой, проходящей через эту точку. Таким образом, дифференциальное уравнение (1') определяет поле направлений на плоскости Оху.
 При различных значениях С получаем различные изоклины. Уравнение изоклины, соответствующей значению С, будет, очевидно, f (x, у)= С. Построив семейство изоклин, можно приближенно построить семейство интегральных кривых. Говорят, что, зная изоклины, можно качественно определить расположение интегральных кривых на плоскости.
При различных значениях С получаем различные изоклины. Уравнение изоклины, соответствующей значению С, будет, очевидно, f (x, у)= С. Построив семейство изоклин, можно приближенно построить семейство интегральных кривых. Говорят, что, зная изоклины, можно качественно определить расположение интегральных кривых на плоскости. (3)
(3)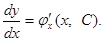 (4)
(4)


