
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные уравнения второго порядка с постоянными коэффициентами
Имеем линейное однородное уравнение второго порядка
где р и q — постоянные действительные числа. Чтобы найти общее решение этого уравнения, достаточно, как было доказано выше, найти два линейно независимых частных решения. Будем искать частные решения в виде у = еkх,где k = const; (49) тогда
Подставляя полученные выражения производных в уравнение (48), находим:
Так как k 2 +pk + q = 0. (50) Следовательно, если k будет удовлетворять уравнению (50), то еkх будет решением уравнения (48). Уравнение (50) называется характеристическим уравнением по отношению к уравнению (48). Характеристическое уравнение есть квадратное уравнение, имеющее два корня: обозначим их через k 1и k 2. При этом
Возможны следующие случаи: I. k 1и k 2 — действительные и II. k 1и k 2 — комплексные числа; III. k 1и k 2 — действительные равные числа Рассмотрим каждый случай отдельно. I. Корни характеристического уравнения действительны и различны:
Эти решения линейно независимы, так как Следовательно, общее решение имеет вид
Пример 1. Дано уравнение ○ Характеристическое уравнение имеет вид Находим корни характеристического уравнения:
По формуле (51) общее решение: II. Корни характеристического уравнения комплексные. Так как комплексные корни входят попарно сопряженными, то обозначим:
Воспользовавшись формулой Эйлера:
Функции у 1и у 2 линейно независимы, но содержат мнимую единицу. Чтобы получить действительные частные решения рассмотрим линейные комбинации функций у 1и у 2:
Получим:
Решения Следовательно, общее решение уравнения (48) в случае комплексных корней характеристического уравнения имеет вид:
Важным частным случаем решения (52) является случай, когда корни характеристического уравнения чисто мнимые. Это имеет место тогда, когда в уравнении (48) р = 0,и оно имеет вид
Характеристическое уравнение (50) принимает вид
Корни характеристического уравнения
Решение (52) принимает вид
III. Корни характеристического уравнения действительные и равные. Обозначим Одно частное решение
Проверим, что функция
Подставляя выражения производных в уравнение (48), получаем
Так как k – корень характеристического уравнения, то Решение Поэтому общим решением будет функция
Пример 2. Дано уравнение ○ Пишем характеристическое уравнение Линейные однородные уравнения п -го порядка с постоянными Коэффициентами Рассмотрим линейное однородное уравнение п -го порядка:
Будем предполагать, что а 1, а 2,..., ап — постоянные. Прежде чем указывать метод решения уравнения (54), введем определение, нужное нам для дальнейшего. Определение. Если для всех х отрезка
где A 1, А 2,..., Ап — постоянные числа, не все равные нулю, то говорят, что Определение. п функций Замечание 1. Из определений следует, что если функции
Пример. Функции
не будет тождественно равно нулю. Перейдем теперь к решению уравнения (54). Для этого уравнения справедлива следующая теорема. Теорема. Если функции у = С 1 у 1 + С 2 у 2+....+ Спуп (55) где С 1,..., Сп — произвольные постоянные. Если коэффициенты уравнения (54) постоянны, то общее решение находится так же, как и в случае уравнения второго порядка. 1) Составляем характеристическое уравнение
2) Находим корни характеристического уравнения 3) По характеру корней выписываем частные линейно независимые решения, руководствуясь тем, что: а) каждому действительному однократному корню k соответствует частное решение еkх;
б) каждой паре комплексных сопряженных однократных корней в) каждому действительному корню k кратности r соответствует r линейно независимых частных решений
г) каждой паре комплексных сопряженных корней кратности s соответствуют 2 s частных решений:
Этих частных решений будет ровно столько, какова степень характеристического уравнения (т. е. столько, каков порядок данного линейного дифференциального уравнения). Можно доказать, что эти решения линейно независимы. 4) Найдя п линейно независимых частных решений y 1, y 2,..., уп, строим общее решение данного линейного уравнения:
Пример. Найти общее решение уравнения ○ Составляем характеристическое уравнение Находим корни характеристического уравнения:
Записываем общее решение:
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.213.235 (0.02 с.) |
 , (48)
, (48)
 .
. , то, значит,
, то, значит, .
. ;
; .
. .
. .
. . (51)
. (51) .
.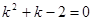 .
.
 .●
.● .
. , запишем частные решения в виде
, запишем частные решения в виде ,
, .
. .
. .
.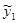 и
и 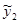 линейно независимы, т.к.
линейно независимы, т.к. 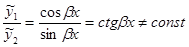 .
. . (52)
. (52) .
.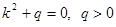 .
. .
. .
. .
. получается на основании предыдущих рассуждений. Нужно найти второе частное решение, линейно независимое с первым.
получается на основании предыдущих рассуждений. Нужно найти второе частное решение, линейно независимое с первым. является решением уравнения (48). Дифференцируя, находим:
является решением уравнения (48). Дифференцируя, находим: .
.

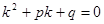 , кроме того
, кроме того 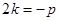 , поэтому
, поэтому  .
. .
. . (53)
. (53)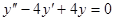 .
. . Находим его корни:
. Находим его корни:  . Общим интегралом будет:
. Общим интегралом будет:  .●
.●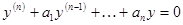 . (54)
. (54) имеет место равенство
имеет место равенство ,
,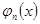 выражается линейно через функции
выражается линейно через функции  .
. называются линейно независимыми, если никакая из этих функций линейно не выражается через остальные.
называются линейно независимыми, если никакая из этих функций линейно не выражается через остальные.
 линейно независимы, так как ни при каких С 1, С 2, С 3, одновременно не равных нулю, выражение
линейно независимы, так как ни при каких С 1, С 2, С 3, одновременно не равных нулю, выражение
 являются линейно независимыми решениями уравнения (54), то его общее решение есть
являются линейно независимыми решениями уравнения (54), то его общее решение есть .
. .
. и
и  ;
; ;
;
 .
. .
.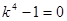 .
. .
. .
.


