
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения высших порядков (общие понятия)
Дифференциальное уравнение п -го порядка символически можно записать в виде
или, если его можно разрешить относительно п -й производной,
Для уравнений, которые можно разрешить относительно высшей производной имеет место теорема о существовании и единственности решения, аналогичная соответствующей теореме о решении уравнения первого порядка. Теорема. Если в уравнении
функция
то существует и притом единственное решение у = у (х) уравнения, удовлетворяющее условиям
Эти условия называются начальными условиями. Если рассматривать уравнение второго порядка
то начальными условиями при
где Определение. Общим решением дифференциального уравнения п -го порядка называется, функция
зависящая от п произвольных постоянных С 1, С 2,..., Сп и такая, что: а) она удовлетворяет уравнению при любых значениях постоянных С 1, С 2,..., Сп; б) при заданных начальных условиях
постоянные С 1, С 2,..., Сп можно подобрать так, что функция Соотношение вида Всякая функция, получающаяся из общего решения при конкретных значениях постоянных С 1, С 2,..., Сп называется частным решением. График частного решения называется интегральной кривой данного дифференциального уравнения. Далее рассмотрим методы решения некоторых видов д.у. высших порядков. I. Уравнение вида Простейшим уравнением п -го порядка является уравнение вида
Найдем общий интеграл этого уравнения.
Интегрируя по х левую и правую части, получим:
Интегрируя еще раз, получим:
Продолжая далее, получим, (после п интегрирований), выражение общего интеграла:
где
Так как
Пример. Найти частное решение уравнения ○ Найдем общее решение последовательным интегрированием данного уравнения:
Чтобы найти частное решение, удовлетворяющее данным начальным условиям, достаточно определить соответствующие значения С 1 и С 2. Из условия Таким образом, искомое частное решение имеет вид
II. Уравнение вида
не содержит явным образом искомой функции у. Порядок такого уравнения можно понизить, взяв за новую неизвестную функцию низшую из производных данного уравнения, т.е. полагая
Таким образом, порядок уравнения понизился на k единиц. Уравнение второго порядка, разрешенное относительно наивысшей производной, данного вида имеет вид
Рассмотрим его решение. Обозначим производную
относительно неизвестной функции z от х. Проинтегрировав это уравнение, находим его общее решение:
а затем из соотношения
Пример. Найти общее решение уравнения ○ Полагаем
Это однородное уравнение первого порядка. Полагая
В полученном уравнении разделяем переменные и интегрируем:
Т.к.
III. Уравнение вида
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.181.231 (0.012 с.) |
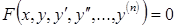 . (33)
. (33)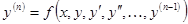 ( 33 ')
( 33 ')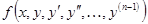 и ее частные производные по аргументам у, у ',..., у (п -1) непрерывны в некоторой области D пространства(п +1) мерности, содержащей значения
и ее частные производные по аргументам у, у ',..., у (п -1) непрерывны в некоторой области D пространства(п +1) мерности, содержащей значения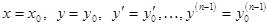 ,
,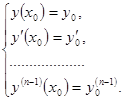 (34)
(34)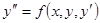
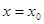 для решения будут условия
для решения будут условия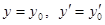 ,
, — заданные числа. Геометрический смысл этих условий следующий: через заданную точку плоскости
— заданные числа. Геометрический смысл этих условий следующий: через заданную точку плоскости 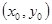 с заданным тангенсом угла наклона касательной
с заданным тангенсом угла наклона касательной  проходит единственная кривая. Из этого, далее, следует, что если мы будем задавать различные значения
проходит единственная кривая. Из этого, далее, следует, что если мы будем задавать различные значения  и
и 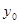 то получим бесчисленное множество интегральных кривых с различными углами наклона, проходящих через заданную точку.
то получим бесчисленное множество интегральных кривых с различными углами наклона, проходящих через заданную точку.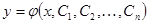
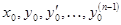 принадлежат к области D, где выполняются условия существования решения).
принадлежат к области D, где выполняются условия существования решения).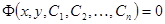 , неявно определяющее общее решение, называется общим интегралом дифференциального уравнения.
, неявно определяющее общее решение, называется общим интегралом дифференциального уравнения.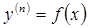
 (35)
(35)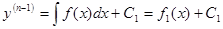 .
.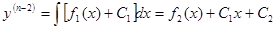 ,
,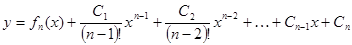 ,
, .
.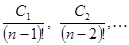 являются постоянными величинами, то общее решение может быть записано так:
являются постоянными величинами, то общее решение может быть записано так: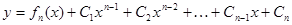 .
.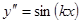 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  .
.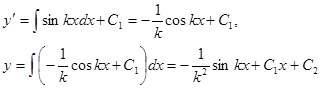
 находим С 2 = 0. Из условия
находим С 2 = 0. Из условия  находим С 1= l.
находим С 1= l. .●
.●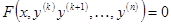 , (36)
, (36)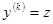 . Тогда получим уравнение
. Тогда получим уравнение .
.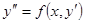 . (37)
. (37)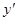 через z, тогда
через z, тогда 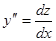 . Подставляя эти выражения производных в уравнение (37), получим уравнение первого порядка
. Подставляя эти выражения производных в уравнение (37), получим уравнение первого порядка
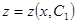 ,
,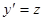 получаем общий интеграл уравнения (37):
получаем общий интеграл уравнения (37):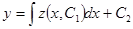 .
.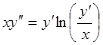 .
. , преобразуем уравнение к виду
, преобразуем уравнение к виду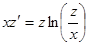 или
или 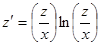 .
.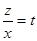 , откуда
, откуда  , получим уравнение
, получим уравнение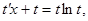
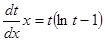 .
.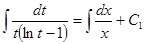 .
.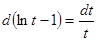 , то имеем
, то имеем 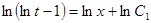 , или
, или  , откуда
, откуда 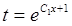 . Следовательно,
. Следовательно, (выше был использован метод интегрирования «по частям»).
(выше был использован метод интегрирования «по частям»).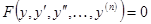 , (38)
, (38)


