
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение в полных дифференциалах
Определение. Уравнение M (x, y) dx + N (x, y) dy = 0(27) называется уравнением в полных дифференциалах, если М (х, у)и N (х, у)— непрерывно-дифференцируемые в области D функции, для которых выполняется соотношение
Интегрирование уравнений в полных дифференциалах. Докажем, что если левая часть уравнения (27) есть полный дифференциал, то выполняется условие (28), и обратно — при выполнении условия (28) левая часть уравнения (27) есть полный дифференциал некоторой функции u(x, у),т. е. уравнение (27) имеет вид du (x, y) = 0(29) и, следовательно, его общий интеграл есть и (х, у) = С. Предположим сначала, что левая часть уравнения (27) есть полный дифференциал некоторой функции и (х, у),т. е. M (x, y) dx+N (x, y) dy = du= тогда
Дифференцируя первое соотношение по у, а второе — по х, получим:
Предполагая непрерывность вторых производных, будем иметь
находим:
где х 0— абсцисса любой точки из области существования решения. При интегрировании по х мы считаем у постоянным и поэтому произвольная постоянная интегрирования может зависеть от у. Подберем функцию С (у)так, чтобы выполнялось второе из соотношений (30). Для этого продифференцируем обе части последнего равенства по у и результат приравняем к N (x, y): но в силу (28) можем написать:
Следовательно,
или
Таким образом, функция и (х, у) будет иметь вид
Здесь P (x 0, y 0) — точка, в окрестности которой существует решение Итак, общий интеграл уравнения (27) имеет вид
Пример. Дано уравнение
○ Проверяем условие (28). Обозначим
тогда
Условие (28) при Найдем общий интеграл уравнения по формуле (32) взяв х 0=0, у 0=1.
Подставляя пределы интегрирования, находим
Замечание. При решении уравнений в полных дифференциалах вместо использования формулы (32) можно непосредственно применить алгоритм, с помощью которого она получена. Поясним этот метод решения на предыдущем примере.
○ Так как
Дифференцируя это соотношение по у и учитывая, что
находим:
следовательно,
Таким образом, общий интеграл исходного уравнения есть
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.103.202 (0.007 с.) |
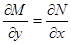 , (28)
, (28) dx+
dx+  dy;
dy; ,
,  . (30)
. (30) .
.
 ,
, ;
; т.е.
т.е.  .
. ,
, .
.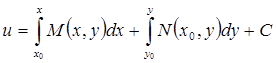 . (31)
. (31)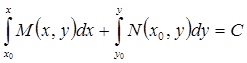 . (32)
. (32)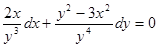 .
. ,
, 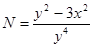 ;
; .
. выполняется. Значит, левая часть данного уравнения есть полный дифференциал некоторой неизвестной функции и (х, у).
выполняется. Значит, левая часть данного уравнения есть полный дифференциал некоторой неизвестной функции и (х, у). , или
, или  .
.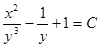 , или
, или  .●
.●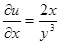 , то следовательно,
, то следовательно,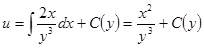 .
. ,
, ;
;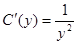 , тогда
, тогда  .
. .●
.●


