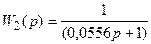Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулировка логарифмического критерияСодержание книги
Поиск на нашем сайте
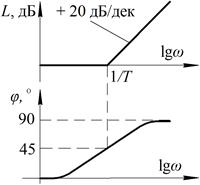
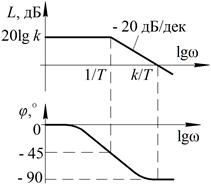
Если разомкнутая система устойчива, то для устойчивости системы в замкнутом состоянии, ЛАХ разомкнутой системы должна пересечь ось абсцисс раньше, чем ЛФХ, спадая окончательно, перейдёт через значение – π. То есть, на частоте среза ωср величина фазы φ должна быть меньше значения | – π |. Запас устойчивости по амплитуде Δ L – это величина допустимого увеличения общего коэффициента усиления разомкнутой системы, при котором замкнутая система окажется на границе устойчивости. Запас устойчивости по фазе Δ φ – это величина допустимого увеличения запаздывания по фазе разомкнутой системы на частоте среза ωср, при котором замкнутая система окажется на границе устойчивости. Для построения ЛАХ и ЛФХ системы необходимо разложить передаточную функцию разомкнутой системы на элементарные звенья, амплитуды А (w) и фазы φ (w) которых приведены в пункте 3.3. Допускается использовать асимптотические ЛАХ, которые графически представляют собой ломаные прямые линии (табл. 3.4).
Таблица 3.4
Асимптотические логарифмические частотные характеристики типовых динамических звеньев
Затем на плоскости строятся ЛАХ и ЛФХ каждого отдельного звена и методом графического суммирования находятся результирующие ЛАХ и ЛФХ разомкнутой системы:
Зная выражения амплитуд А (w) и фаз φ (w) частотных передаточных функции для каждого звена (табл. 3.2), представим их в логарифмическом масштабе (табл. 3.5). Таблица 3.5
Выражения логарифмических амплитуд L (w) и фаз φ (w) передаточных функции звеньев
Вычисляем значения логарифмических амплитуд L (w) и фаз φ (w) для каждого звена при изменении часты w от 0 до значения, при котором результирующая ЛФХ пересекает значение – π. Также вычислим амплитуду LРАЗ (w) и фазу φРАЗ (w) передаточной функции разомкнутой системы WРАЗ (jω). Шаг изменения частоты w принимаем произвольный с учетом удобства восприятия графика. Вычисления проводим в MS Excel. Таблица 3.6
Значения логарифмических амплитуд L (w) и фаз φ (w) передаточных функции звеньев
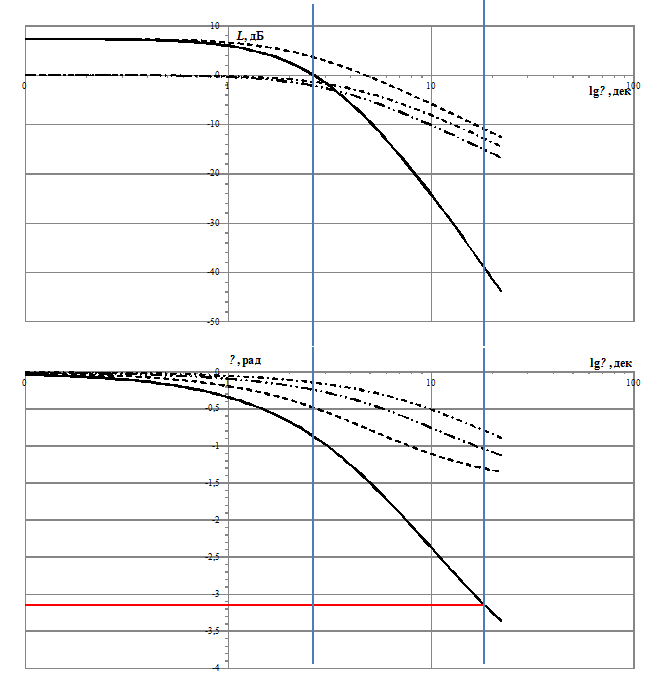
По таблице 3.6 строим логарифмические частотные характеристики системы (рис. 3.3).
Рис. 3.3. Логарифмические частотные характеристики разомкнутой системы (ЛАХ и ЛФХ)
По частотным характеристикам (рис. 3.3) графически определим запасы устойчивости системы: Δ L = **** дБ и Δ φ = **** рад.!!!!!!! Вывод: замкнутая система устойчива, так как ЛАХ разомкнутой системы пересекает ось абсцисс раньше, чем ЛФХ переходит через значение – π.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 205; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.212.244 (0.009 с.) |

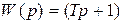

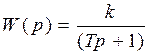

 ; (3.38)
; (3.38)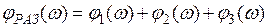 . (3.39)
. (3.39)