Ординалистский подход. Предельная норма замещения. Бюджетная линия. Кривые безразличия.

Предложенная Ф.Эджуортом, В.Парето и И.Фишером порядковая теория полезности позволила обойти стороной те трудности, с которыми столкнулась количественная теория.

В основе своей опирается на ту же теоретическую базу, что и количественный подход.

Порядковый подход основан на менее жестких предпосылках, чем количественный (не требует измерения полезности в абсолютных единицах и постоянства предельной полезности денег). В рамках порядкового подхода от потребителя требуется только ранжировать наборы благ по степени предпочтения. Порядковый подход базируется на следующих аксиомах:

1. Полной (совершенной) упорядоченности. Потребитель может сказать, что А> В (набор А предпочтительнее набора В), либо В> А; либо А ~ В (набор А и набор В равноценны).

2. Транзитивности: если А> В > С или А ~ В ~ С, или А >В ~ С, то А > С.

3. Ненасыщения: если набор А содержит не меньшее количество каждого товара, а одного из них больше, чем набор В, то А > В.

4. Независимости потребителя. Удовлетворение потребителя зависит только от количества потребляемых им благ и не зависит от количества благ, потребляемых другими потребителями.

При порядковом подходе для исследования поведения потребителей пользуются понятиями кривой и карты безразличия.

Кривая безразличия является геометрическим местом точек, каждая из которых представляет такую комбинацию двух товаров, что потребителю безразлично, какую из них выбрать, Множество всех кривых безразличия на плоскости называется картой безразличия.

Свойства кривых безразличия

1. Кривая безразличия, лежащая выше и правее другой кривой, представляет собой более предпочтительные работы товаров. 2. Кривые безразличия для обычных благ имеют отрицательный наклон. 3. Кривые безразличия не пересекаются. 4. Кривые безразличия выпуклы к началу координат.

Люди всегда идут на компромиссы, когда делают выбор между товарами.

Чтобы количественно определить объем некоторого товара, которым потребитель готов пожертвовать ради другого, используется мера, называемая предельной нормой замещения (MRSxy).

Предельной нормой замещения благом Х блага Y называют количество блага Y, которое должно быть сокращено в обмен на увеличение количества блага Х на единицу с тем, чтобы уровень удовлетворения потребителя остался неизменным (U - const):

MRSxy= - (DY/DX) при U = const

Предельная норма замещения может принимать различные значения (0; const; или меняться при движении вдоль кривой безразличия). В случае выпуклости к началу координат MRS убывает по мере замещения одного блага другим.

Кривые безразличия отражают систему предпочтений индивидуума, но для анализа потребительского выбора необходимо учесть ограниченность ресурсов (а именно дохода). Для этого вводится понятие бюджетного ограничения.

Оно показывает, какое количество благ можно приобрести при данных ценах и доходе: I = Рx*X + Py*Y» где I - денежный доход потребителя; Рх и Ру- цены товаров Х и Y. Бюджетная линия - геометрическое место точек, каждая из которых определяет такую комбинацию двух товаров, расходы на которые равны между собой и ограничены доходом потребителя. Уравнение бюджетной линии: Y= (I/Py)-(Px/Py)*X, где (-Рх/Ру) - угловой коэффициент.

При Х=0, Y=I/Py - весь доход потребителя расходуется на благо Y. При Y=0 X=I/Px- весь доход потребителя расходуется на благо X. Наклон бюджетной линии зависит от соотношения цен товаров. Изменения в доходе и ценах вызовут сдвиг бюджетной линии.

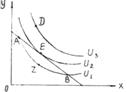
Рис. Равновесие потребителя - точка касания бюджетной линии и кривой безразличия

Условие оптимума потребителя: MRS = - Рх / Ру.

Лекция 9-10. Теория производства экономических благ

Сущность производства. Производственная функция.

Закон убывающей предельной производительности.